可持久话数据结构

可持续化数据结构：
一.可持续化线段树/可持续化数组
核心点：可持久化，可查询历史版本并对历史版本来进行修改
核心算法：动态开点，子节点的利用
关键思想：我们只对修改过的节点进行建新的节点，并且将和原来没有修改过的节点公用一部分节点
每次修改，最多增加logn个节点

见图：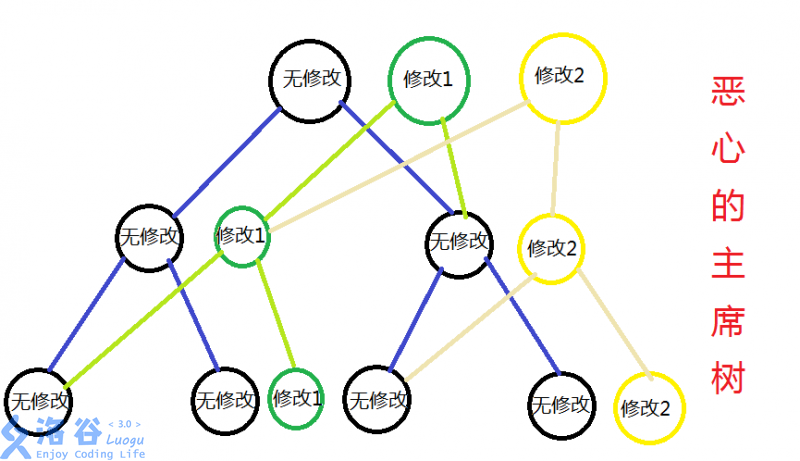

由此我们可以发现
1、每一次修改增加的节点个数为log(n)。

2、增加的非叶子结点会连向一个是其他版本的节点，一个是连向新节点。

3、主席树有很多根……

4、对于每一个根都可以构成一棵完整的线段树。

5、每一个节点都有可能有不只一个父亲节点 $\ \ \ \ \ \ \ 所以我们可以知道主席树只会对部分节点进行复制，并且每一次复制的节点个数是log(n)。我们每一次想询问一个版本的线段树，就可以在那个版本的根构成的线段树中询问。$

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn=1000005*20,maxm=1000005;
int lson[maxn],rson[maxn],a[maxn];
int n,m,cnt;
int temp[maxm],rt[maxm];

void build(int &x,int l,int r)
{
    x=++cnt;
    if(l==r)
    {
        a[x]=temp[l];
        return;
    }
    int mid=l+r>>1;
    build(lson[x],l,mid);
    build(rson[x],mid+1,r);
}
void change(int &x,int l,int r,int pre,int pos,int v)
{
    x=++cnt; 
    if(l==r)//ÒòÎªÊÇµ¥µã²éÑ¯£¬²¢ÇÒÎÒÃÇÔÚÏÂÃæµÝ¹éÒÑ¾ÅÐ¶Ï×óÓÒ£¬ËùÒÔÖ±½ÓÅÐ¶Ï¾Í¿É 
    {
        a[x]=v;
        return;
    }
    int mid=l+r>>1;
    lson[x]=lson[pre];
    rson[x]=rson[pre];
    a[x]=a[pre];//Á¬½ÓµãÐÅÏ¢Ò²ÊÇÒªÒ»²¢¼Ì³Ð 
    if(pos<=mid) change(lson[x],l,mid,lson[pre],pos,v);
    else change(rson[x],mid+1,r,rson[pre],pos,v);
}
int query(int x,int l,int r,int pos)
{
    if(l==r)
    {
        return a[x];
    }
    int mid=l+r>>1;
    if(pos<=mid) return query(lson[x],l,mid,pos);
    else return query(rson[x],mid+1,r,pos); //ÕâÀïµÄreturn ·Ç³£¹Ø¼ü 
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&temp[i]);
    build(rt[0],1,n);
    for(int i=1;i<=m;i++)
    {
        int mod,pos,his;
        scanf("%d%d%d",&his,&mod,&pos);
        if(mod==1)
        {
            int val;scanf("%d",&val);
            change(rt[i],1,n,rt[his],pos,val);
        }
        else
        {
            printf("%d\n",query(rt[his],1,n,pos));
            rt[i]=rt[his];
        }
    
    }
    return 0;
}

View Code

二.主席树

主席树在本质上就是：可持久话的权值线段树，只不过将数据的下标和数值本身的位置进行了一下替换，仅此而已
发明者的原话：“对于原序列的每一个前缀[1···i]建立出一棵线段树维护值域上每个数出现的次数，则其树是可减的”

可以加减的理由：主席树的每个节点保存的是一颗线段树，维护的区间信息，结构相同，因此具有可加减性（关键）

首先开一个数组t[n]，存储内容为a中排序并去重的值（类似于离散化），每棵线段树维护的内容是a1...ai此区间中的树在t[n]中出现的次数
然后我们按照动态开点的写法同样来进行建树，只是不同的是我们这一次的建的是权值线段树，对应的就要使用离散化的技巧
具体看代码的实现

#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;
const int maxn=200000;
struct Node
{
    int val,lc,rc;//其实这里也可以用ch[0]ch[1]来分别表示左右儿子，但是要打一个数组号就很恶心 
}t[maxn*20];//一般需要开刀20倍大 
int cnt,rt[maxn],a[maxn],b[maxn];
int n,m,tot;

void insert(int &x,int l,int r,int pre,int v)
{
    x=++cnt;t[x]=t[pre];t[x].val++;//动态开店，结构体将pre的数据完全复制，因为是前缀和，所以t[x].val++ 
    if(l==r) return;
    int mid=l+r>>1;
    if(v<=mid) insert(t[x].lc,l,mid,t[pre].lc,v);//左右递归，进行重复利用的建树 
    else insert(t[x].rc,mid+1,r,t[pre].rc,v);    
}
int query(int x,int y,int l,int r,int k)
{
    int mid=l+r>>1;
    if(l==r) return l;
    int z=t[t[y].lc].val-t[t[x].lc].val;//关键点，因为结构相似，所以说树上节点的信息可以互相减 
    if(k<=z) return query(t[x].lc,t[y].lc,l,mid,k);
    else return query(t[x].rc,t[y].rc,mid+1,r,k-z);//递归到右边的子树进行寻找，那么排名就要减去作弊那加上中间了 
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[i]=a[i];
    sort(b+1,b+1+n);tot=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;i++)
    {
        a[i]=lower_bound(b+1,b+1+tot,a[i])-b;//
        insert(rt[i],1,tot,rt[i-1],a[i]);//为什么不是1-n呢，因为是离散化过后的权值线段树，所以说最大的范围是在cnt 
    }
    for(int i=1;i<=m;i++)
    {
        int x,y,k;
        scanf("%d%d%d",&x,&y,&k);
        printf("%d\n",b[query(rt[x-1],rt[y],1,tot,k)]);
    }
}

View Code

注意按照左大右小这种方式插入的时候（平衡树，或者权值线段树），在向右节点递归的时候，一定要减去左节点和中节点的size

https://www.cnblogs.com/hanruyun/p/9916299.html

https://blog.csdn.net/ModestCoder_/article/details/90107874

https://www.luogu.com.cn/problem/solution/P3919

https://blog.csdn.net/ModestCoder_/article/details/90107874

posted @ 2020-09-16 12:44 ILH 阅读(184) 评论(0) 收藏举报

刷新页面返回顶部

可持久话数据结构

公告