高级数据结构 2

根号算法

莫队算法：【日报上有可以在线的莫队】

莫队算法主要是用于离线解决通常不带修改只有查询的一类区间问题。
考虑到时间复杂度，如果我们使用线段树来维护这一区间以及相关的信息，我们会发现，每一个节点都是需要update才能得到相应的区间，换而言之，我们不能在O（1）的算法（或者复杂度极低）当中得到我们所想要的答案
莫队的本质实际上是通过优化搜索顺序得到巧秒剪枝， $一种思想化的算法，是一种将询问放在一起考虑，基于分块实现操作$
我们对于一个区间[l,r]我们已经知道了这一区间的相关信息，如果我们不进行优化。那么两个区间的信息转移复杂度就是两点的曼哈顿距离
$首先，如果要用莫队算法，则必须满足已知ans[l,r]$ 那么对于[l,r+1]我们只需要再合并a[r+1]的信息，而合并的过程就是O（1）的，那么[l,r]就可以扩展到[l+1/-1,r+1/-1]四种方向上进行；莫队要做的，就是对搜索顺序进行优化，使我们要查询的区间按照更为合理的扩展顺序进行合并和搜索
粗略的实现方法： $1 . 先对原序列分块，一般分为tot=sqrt(n)$ 复杂度O(m+n跟下m）
莫队算法的小优化：奇偶块排序** 莫队算法比较重要的东西是对询问排序但是排序也是有讲究的莫队算法一般的排序方式是这样的： ```cpp bool cmp(query x,query y) { return (x.r/tot)==(y.r/tot)?x.l<y.l:x.r<y.r; } ``` 而有一种神奇的排序方式叫做奇偶块排序，它长这样： ```cpp bool cmp1(query x,query y) { return (x.l/tot)^(y.l/tot)?x.l<y.l:(((x.l/tot)&1)?x.r<y.r:x.r>y.r); } ``` 由于chen_zhe过于毒瘤，导致现在几乎没有几道莫队题用普通排序能通过了$233 $ 奇偶块排序会快的原理貌似是因为在普通排序之后，指针会出现跳回左边的情况后，而为了处理下一个块又要跳回右边，但经过奇偶块排序之后，指针移到右边后就不用再跳回左边，所以这样能减少很多（一半）操作，理论上能快一倍
$考虑在指针移动时其实就是加入和删除贝壳的过程。加入贝壳时对于一种颜色x$
https://blog.csdn.net/chiyankuan/article/details/95663759（简单的总结）https://www.cnblogs.com/WAMonster/p/10118934.html（莫队介绍）
https://www.luogu.com.cn/blog/new2zy/qian-tan-gen-hao-suan-fa-fen-kuai（分块+莫队）
只撤销不删除的莫队：无法进行删除操作的时候，维护某个块的做断电，我们可以先在右端点进行插入，直到移动到询问区间的右端点的时候，我们将左端点未插入的元素插入，计算贡献之后再将其删除就可以了
带修莫队：原本是左端点分块，右端点跑一边，现在可以左右端点都分块，按照时间轴来跑一边块的个数 O（n^1/3）,操作O（n^5/3）【这个东西和暴力已经差不多了】
首先，我们来看普通莫队的实现:以P3267为例子

对于排序，我们有以下的代码：

int cmp(query a, query b) {
    return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
}

View Code

如果需要使用奇偶性优化，我们可以

int cmp(query a, query b) {
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

View Code

也就是说，对于左端点在同一奇数块的区间，右端点按升序排列，反之降序。这个东西也是看着没用，但实际效果显著。

2、定策略

虽说莫队实质是优化后的暴力，但有时候，有些用暴力枚举很容易处理的数据用莫队并不容易处理（只能在左右指针处更新），这时候就要我们定好一个更新策略。
一般来说，我们只要找到指针移动一位以后，统计数据与当前数据的差值，找出规律（可以用数学方法或打表），然后每次移动时用这个规律更新就行啦qwq。至于例题……在后面会有哒qwq！

3、码代码与查错

莫队代码不长（或者说是很短），但很容易写错一些细节。比如自加自减运算符的优先级问题、排序关键字问题、分块大小与sqrt精度问题、还有某些题目中用到的离散化的锅。所以每次码完莫队都别先测样例（甚至可以先不编译），先静态查错一阵，真的可以帮助你大大减少错误的发生。

3、移动指针的常数压缩

3、移动指针的常数压缩
我们可以根据运算优先级的知识，把这个：

void add(int pos) {
    if(!cnt[aa[pos]]) ++now;
    ++cnt[aa[pos]];
}
void del(int pos) {
    --cnt[aa[pos]];
    if(!cnt[aa[pos]]) --now;
}
和这个：

while(l < ql) del(l++);
while(l > ql) add(--l);
while(r < qr) add(++r);
while(r > qr) del(r--);
硬生生压缩成这个：

while(l < ql) now -= !--cnt[aa[l++]];
while(l > ql) now += !cnt[aa[--l]]++;
while(r < qr) now += !cnt[aa[++r]]++;
while(r > qr) now -= !--cnt[aa[r--]];

在这里我们补充两个小的知识点

ceil函数：ceil(number)向上舍入最接近的整数，floor（number）向下舍入最接近的整数，round（num，tot）ROUND 函数用于把数值字段舍入为指定的小数位数。
由此我们可以得到这一中莫队的标准程序

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;

#define maxn 1010000
#define maxb 1010
int aa[maxn], cnt[maxn], belong[maxn];
int n, m, size, bnum, now, ans[maxn];
struct query {
    int l, r, id;
} q[maxn];

int cmp(query a, query b) {
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);//前面一个：两者的奇偶性是否不同，后面一个，按照奇偶性决定右端点的升序或者降序 
}
#define isdigit(x) ((x) >= '0' && (x) <= '9')
int read() {
    int res = 0;
    char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar();
    return res;
}
void printi(int x) {
    if(x / 10) printi(x / 10);
    putchar(x % 10 + '0');
}

int main() {
    scanf("%d", &n);
    size = sqrt(n);
    bnum = ceil((double)n / size);
    for(int i = 1; i <= bnum; ++i) //一共需要分成多少块 
        for(int j = (i - 1) * size + 1; j <= i * size; ++j) {//计算每一个下标对应的是哪一个块 
            belong[j] = i;
        }
    for(int i = 1; i <= n; ++i) aa[i] = read(); 
    m = read();
    for(int i = 1; i <= m; ++i) {
        q[i].l = read(), q[i].r = read();
        q[i].id = i;//这是第几个询问，排序后乱序，故id一定呀存储 
    }
    sort(q + 1, q + m + 1, cmp);
    int l = 1, r = 0;
    for(int i = 1; i <= m; ++i) {
        int ql = q[i].l, qr = q[i].r;
        while(l < ql) now -= !--cnt[aa[l++]];
        while(l > ql) now += !cnt[aa[--l]]++;
        while(r < qr) now += !cnt[aa[++r]]++;
        while(r > qr) now -= !--cnt[aa[r--]];
        ans[q[i].id] = now;
    }
    for(int i = 1; i <= m; ++i) printi(ans[i]), putchar('\n');
    return 0;
}

View Code

根号平衡：

前提：再操作中我们一般有修改和询问两端：有可能一端是O(n跟下n) 另一端是O（n）这个时候我们就要使用一下三种情况以一边跟下n的代价换取另一边的O1保证都不会超过复杂度【相比log数据】也就是说n跟下nlog级别的复杂度基本上是会被卡掉的
$O (\sqrt{N})$

首先思考

同样的，在块内，快外分别维护前缀和，每次修改更新

维护块内和，每次修改块内和和该位置的值

直接分块，在块上大区间加标记

维护差分数组即可

值域分块，维护区间加

仍然用值域分块，维护每个数在那个位置，保证每个块内为

每次查询修改

查询时定位位置即可

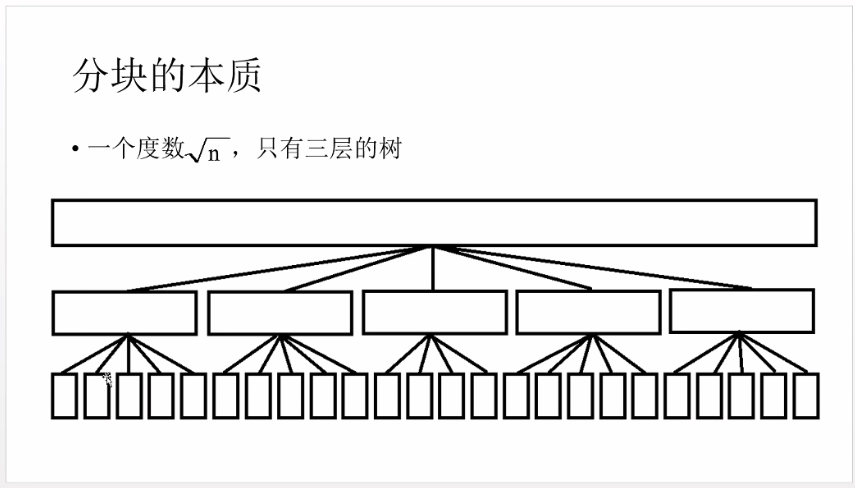
分块

何为分块？从本质上讲，分块也是一种优雅的暴力型式，将一整段区间上的元素划分成若干个块（可以证明当块的大小是sqrt(n)）的时候是最优的，此时我们将预处理的信息保存下来，以空间换取时间
基本操作：分块实际上是把区间操作放在了整块【区间被完全包含在块中】以及不完整的块【也就是左右段点所在的块中】
“数列分块就是把数列中每m个元素打包起来，以达到优化算法的目的。”——hwzer
通常来说，分块的操作一般分为：分块实现的基本框架：
划分块，预处理，操作或查询。
操作或查询通常为4步：
1.判断要操作或是查询的区间是否在一个块内
2.若在一个块内，暴力操作或查询
3.若不在一个块内，将除了最左边和最右边这两个块外其余的块进行整体的操作，即直接对块打上修改标记之类的
4.单独暴力处理最左边的块和最右边的块
注意：根号平衡的算法都自带二倍常数！

这也是为什么分块往往能保证正确性，但是执行的效率很低很低的原因
对于每次区间操作：

1.不完整的块的O(√n)个元素怎么处理？

2.O(√n)个整块怎么处理？

3.要预处理什么信息（复杂度不能超过后面的操作）？（通常是块所需要储存的信息）

　　 4.查询时怎么样查询所要的信息：合并？比较？拆分？

对于分块和线段树以及树状数组的比较，分块是根号级别，对于log级别的数据结构不占优势，但是简单的东西其可拓展性也就越强，换而言之，分块是一种强大的思想模型（如同分治一般）
同时，分块的空间大小也是比线段树小的不能再小了，同时打起来也超级方便的；
总而言之，分块即思想；
https://www.cnblogs.com/ywjblog/p/9481012.html（分块的简单介绍）http://hzwer.com/8053.html（hzwer的分块九题）
分块的调试检测技巧：

可以生成一些大数据，然后用两份分块大小不同的代码来对拍，还可以根据运行时间尝试调整分块大小，减小常数。
问题1:块数过大，假使涉及到单点插入等操作，可能会使得原来的块不平衡，而导致某一个块超过了跟下n，复杂度自然会退化:
解决方法：1.对于每跟下n次插入过后，我们对于这些数进行重新分块

　　　　　　　　2.在插入的时候进行判断，如果发现某一个块过大就重新分配或者直接把他拍成两个快（同时进行下标移动）

　　重构需要的复杂度为O(n)，重构的次数为√n，所以重构的复杂度没有问题，而且保证了每个块的大小相对均衡。

问题2：多个标记同时处理时，要关注几个标记的优先程度：

　　　解决方法：假如说有加法标记和乘法标记,我们每次修改之后要知道新的加法和乘法标记怎么样才是等价的

　　　举例：

　　　　若当前的一个块乘以m1后加上a1，这时进行一个乘m2的操作，则原来的标记变成m1*m2，a1*m2（加的那一部分也要翻倍，乘的那一部分也要翻倍）

　　　　若当前的一个块乘以m1后加上a1，这时进行一个加a2的操作，则原来的标记变成m1，a1+a2　　（这一步比较好理解）

问题3：给出一个长为n的数列，以及n个操作，操作涉及区间询问等于一个数c的元素，并将这个区间的所有元素改为c。
解决方法：
我们思考这样一个暴力，还是分块，维护每个分块是否只有一种权值，区间操作的时候，对于同权值的一个块就O(1)统计答案，否则暴力统计答案，并修改标记，不完整的块也暴力。

这样看似最差情况每次都会耗费O(n)的时间，但其实可以这样分析：

假设初始序列都是同一个值，那么查询是O(√n)，如果这时进行一个区间操作，它最多破坏首尾2个块的标记，所以只能使后面的询问至多多2个块的暴力时间，所以均摊每次操作复杂度还是O(√n)。

换句话说，要想让一个操作耗费O(n)的时间，要先花费√n个操作对数列进行修改。
问题4：众数问题（参考陈立杰的论文）
http://hzwer.com/3671.html（相关题目）
引入思想：由无至有：当多个条件严格限制，我们难以设计算法时，不妨先减少限制的条件数量，然后再简单的算法结构上进行优化和补充
解决方法：具体思想仍就是考虑出如何合并以及维护

　　　当没有修改的时候，我们知道集合a∪b的众数是mode(a)∪b，这是毫无疑问的，所以对于我们的分块，最多处理的是三部分左残，中整，右残，且左右的处理不会超过(2根号n）

　　　当有修改的时候，为了简洁，我们需要做的是在O（1）范围内知道[l,r]内x出现了几次，想都不用想就是维护前缀和，

　　　对于不完整的块，我们可以维护其前k个当中x出现了多少次（因为我们也维护了整个块的，所以后面的也是成立的）

　　　当有修改的时候，我们发现，一次修改可能会影响到O（L^2）L为分块的个数，此时就退化了

这个时候我们就需要考虑
问题5：分块大小一定是sqrt（n）吗？

　　　实际上，当我们仔细分析，3根n才是最合适的分块大小

　　　也就是说，不一定有固定的最优分块大小，可以通过猜测，题目分析，以及对拍来进行实现

　　下面给出一道例题的代码

#include<bits/stdc++.h>
using namespace std;
const int N=50050;
int n;
struct Block{  //结构体储存函数和变量
    int a[N],k,len,L[N],R[N],F[N],add[N];
    //变量介绍：a[N]记录数列，k指块的数目，len指块的长度
   // L[N]记录每个块起始元素的下标，R[N]记录每个块末尾元素的下标
   // F[N]记录每一个元素所属哪一个块，add[N]也就是加法标记
    inline void Build(){  //建块
        memset(a,0,sizeof(a));
        memset(add,0,sizeof(add));
        for(int i=1;i<=n;i++)
            scanf(“%d”,&a[i]);  //输入原数列
        len=sqrt(n); k=n/len;  //计算块的长度和数目
        if(n%k) k++;   //特判最后一个不完整块
        for(int i=1;i<=k;i++)
            R[i]=i*len,L[i]=R[i-1]+1;  //计算每个块起始和末尾元素的下标
        R[k]=n;  //特判最后一个块的末尾下标为n
        for(int i=1;i<=k;i++)
            for(int j=L[i];j<=R[i];j++)
                F[j]=i;  //计算每一个元素所属哪一个块
    }
    inline void Add(int x,int y,int z){  //区间加法
        if(F[x]==F[y]){  //如果区间被包含于一个整块
            for(int i=x;i<=y;i++) a[i]+=z;  //直接上传加法标记
            return;  //返回即可
        }
         //如果区间跨过整块
        for(int i=x;i<=R[F[x]];i++) a[i]+=z;   //把左边的不完整块的元素值直接改变
        for(int i=L[F[y]];i<=y;i++) a[i]+=z;   //把右边的不完整块的元素值直接改变
        for(int i=F[x]+1;i<F[y];i++) add[i]+=z;  //最后改变夹在中间整块的加法标记
    }
    inline int Ask(int x){  //单点询问
        return a[x]+add[F[x]];  //直接输出原数列的值和块的加法标记
    }
}B;
signed main(){
    scanf(“%d”,&n);
    B.Build();  //建块
    for(int i=1,opt,l,r,c;i<=n;i++){
        scanf(“%d%d%d%d”,&opt,&l,&r,&c);
        if(!opt) B.Add(l,r,c);  //区间加法
        else printf(“%d\n”,B.Ask(r));  //单点询问
    }
    return 0;
}

View Code

根号分治

基本概念：对于若干个正整数和为n，我们知道其中大于l的数不超过[n/l]个（显然【n/l】）
所以我们分治的思想就是用f(n)的复杂度维护一个大于l的数，用g(n)的复杂度来维护一个不大于l的数，【这个时候显然f可以稍微大一些，而g一般要小一些，这样整体是平衡的】
经典例子：
1.度数分治
对于一张无向图，边数m，那么其度数和就一定是2*m，（也就是上文的和为n），此时我们发现，度数比较大的点比较少，度数比较小的点一大堆【菊花图就是典型例子】
所以说度数大的点不会超过根号m个，度数小的不会少于根号m个，那么对于大的点我们可以直接暴力修改，对于小的点我们按照它的度数来进行维护
修改点权：求每一个点的相邻点的权值和（如果是树就很简单），在图上呢？
2.颜色数分治
颜色数大于根号的颜色最多只有根号种，剩下的颜色的颜色数都是小于根号的
出现次数大于根号的颜色单独处理，小于根号的按照出现次数为代价来处理
先算出来大颜色到每个其他颜色的距离，都小于的话我们可以直接归并处理（因为之前的时候）

根号重构

建立一个静态的数据结构（静态就意味着不支持修改），并且维护每一个每一次修改所做出的贡献，当修改次数达到了l次的时候，我们直接重新构建数据结构
重构用f(n),计算用g(l)，那么时间复杂度就是O(mg(l)+m/l*f(n))，最优复杂度是O（m根号n）
在本质意义上就是时间轴上的分块
题目：P2137 给一棵树，修改点权，插入节点，求字树种大于x的数的个数
添加节点之后，dfs就被破坏了，就非常难受了
若没有修改，那么就是一个二维数点问题，一个主席树【主席树就是静态结构】就可以水过去了
设l=根号下logn【这里是根据f(n)来计算l取什么】）
树分块是非常恐怖了，但是按照时间分块是比较简单的，其实我们也可以使用dfn括号序

杂项

P3224：点权图，每次连边，求连通块点权的k小值
可以离线并查集维护：每次的连通块标记成连续的区间（麻烦），再建主席树

启发式合并（通用）

复杂度比较客观：两个数据结构怎么合并呢？
将元素个数较少的数据结构暴力插入到另一个数据结构当中，
被插入时，空间至少扩大一倍每个元素最多被插入logn次，如果一次插入要logn，那么总体的复杂度是O(nlog^2n)
每一个用平衡树，那么空间是O（n）【需要内存回收】
SPLAY具有自适应性O（nlogn）但是常数比较大

线段树合并

前提：动态开点合并相同区间对应的节点，如果是空树就合并，否则就要递归合并两棵字树
复杂度：之和合并后减少的节点数有关， O（nlogV）（V是权值【很多时候是用来搞权值的，权值大的话不能离散化】）
最初就要用掉O（nlogn）的空

题目：序列，某个区间排序，单点查询【如果要升降序的话需要维护一些翻转标记】

线段树分裂

平衡树的话反复分裂再合并的话就一定是炸掉的
分裂增加的节点是小于等于V和大于V的，考虑V和V+1到根的路径，只会在这两个上面增加
最多增加O（logV）个节点【也就是增加的点数不太多，那么合并的代价也不会太多】
所以任意分裂合并的复杂度还是O（nlogV）【V是值域】
对每一个位置开一课线段树，然后只插入一个节点，排序的话就把线段树合并了，排序的话按照值域合并的自然就有序了
每暴力合并一次，树的颗数会减少一颗，如果合并的时候遇到了已经合并的话，就把他分裂成两棵【一颗在区间内，一颗在区间外】
把两个端点分裂，然后再中间合并

动态图连通性

给一张图，插一条边【只加就直接并查集】，删一条边，查询两点是否联通，可以离线
常用转化【一般要求各最小生成树啥的】
LCT的经典用处：维护只加边的最小生成树（也就是说我们可以维护删去的时间作为边权，然后维护最大生成树）常数很大啊

线段树分治

解决问题：如果某些东西存在的时间是一个区间，并且可以离线的话
线段树拆分区间打标机（维护时间），DFS整颗树，一路上插入或者删除
相当于说，每一个叶子结点回答询问
这里并查集不能删除，但是并查集在DFS就是可以撤销的
补充：【只路径压缩的并查集不能撤销】【安质合并的并查集可以撤销，复杂度O(nlog^2n)】

题目:P4097:维护二维平面上线段的集合，支持插入线段，给出一个k，询问于直线x=k相交的线段中，交点纵坐标最大的线段的编号

【转化模型：区间对每一个等差数列对应位置求最大值，求这个最大值对应的等差数列】【强制在线】

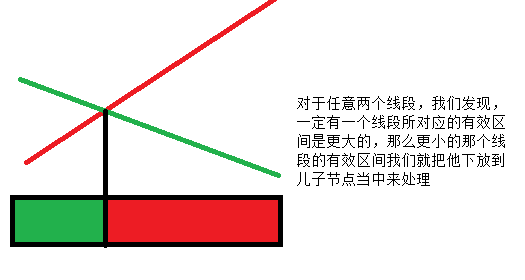
李超线段树

把线段按照x坐标作为标记插入线段树，然后把有效范围较小的线段下放
来张图来举个例子：
也就是一个标记最多下放logn次，每次插入的复杂度是O（log^2n）
查询的时候从叶子到根的这么一条路径，可能有效的线段都可以进行一次计算，然后再里面就可以
这个东西的本质是用来维护半平面交，半平面交的范围是直线，并且更优（对于直线就是整个线段树区间就不用拆开就可以直接下放）
题目：SDOI 2016

可并堆

可以用线段树合并代替：
优势：空间较小，常树较小，并且支持严格复杂度的合并
有很多种，比较容易实现，左偏树->比如斜堆（复杂度是均摊的）【补充：二项堆，斐波那契堆，配对堆，PBDS】
但是支持的操作非常的简单

带删除二叉堆

考虑再开一个堆来维护要删除的元素，一般比std：：multiset快一点

TRIE

是一棵多叉树【字符集大小】，每条边是一个字符
可以把数看成二进制表示的01数集
这样得到的trie是二叉树，可以实现数位的贪心算法，得到的结构和权值线段树完全相同，只是没有计算线段端点【这两个是一个东西】
求异或和最大的区间
压缩trie【不分叉的路径是可以缩成一条边】，这样子节点数仅为O（n）【也就是把整个01trie都记下来】，如果都分叉的话也就是2*n【就是为了压空间罢了】

线性基

一组向量张成空间的一组集再OI中叫线性基
可以动态添加向量，同时用高斯消元更新
二进制数看成向量，异或就可以看成%2的加法，若干个数集可以异或出来的数也就是若干个
特点：通过位长度的区间内仅支持插入的信息，两个线性基不能快速合并，只能暴力插入，最大就是位大小
如果你满了，你就不用合并【可以卡掉一些非常神奇的数据】
只支持插入的刚好就在ll范围内处理

分治预处理

考虑分治树，对于每个节点，预处理出[l.m][m+1,r]子节点的信息，m=l+r>>1;整个过程是O(nlogn）
写就是处理出来了左区间的后缀，右区间的前缀的信息
也就是对应任何查询区间[l,r],分治树上总可以找到一个对应区间包含[l,r]，且中电m在[l,r]内的节点，将预处理的[,m]和[m+1,r]进行合并，就可以得到答案
直接查找事O（logn）的，如果把它长度扩充到2的幂次的话，就可以使用位运算将复杂度化成O(1)
和线段树对比，线段树要进行的是log次合并，相对比的话它只需要进行一次合并
除非查询次数远大于序列长度，所以只能O（1）
无修，合并代价比较高的东西比较使用

posted @ 2020-08-29 16:58 ILH 阅读(228) 评论(0) 收藏举报

刷新页面返回顶部

高级数据结构 2

根号算法

莫队算法：【日报上有可以在线的莫队】

只撤销不删除的莫队：无法进行删除操作的时候，维护某个块的做断电，我们可以先在右端点进行插入，直到移动到询问区间的右端点的时候，我们将左端点未插入的元素插入，计算贡献之后再将其删除就可以了

带修莫队：原本是左端点分块，右端点跑一边，现在可以左右端点都分块，按照时间轴来跑一边 块的个数 O（n^1/3）,操作O（n^5/3）【这个东西和暴力已经差不多了】

2、定策略

3、码代码与查错

3、移动指针的常数压缩

根号平衡：

O(N−−√)O(N)单点修改，O(1)O(1)查询区间和

O(1)O(1)单点修改，O(N−−√)O(N)查询区间和

O(N−−√)O(N)区间加，O(1)O(1)查询单点值

O(1)O(1)区间加，O(N−−√)O(N)查单点

O(1)O(1)插入一个数，O(N−−√)O(N)查询第k小

O(N−−√)O(N)插入一个数，O(1)O(1)查询第k小

分块

注意：根号平衡的算法都自带二倍常数！

根号分治

根号重构

杂项

启发式合并（通用）

线段树合并

线段树分裂

动态图连通性

线段树分治

李超线段树

可并堆

带删除二叉堆

TRIE

线性基

分治预处理

公告

带修莫队：原本是左端点分块，右端点跑一边，现在可以左右端点都分块，按照时间轴来跑一边块的个数 O（n^1/3）,操作O（n^5/3）【这个东西和暴力已经差不多了】

$O (\sqrt{N})$