P3327 约数个数和
题意:
首先,我们给出一个结论: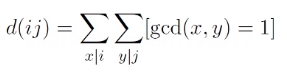
证明如下:1.对于给出的每一组互质的i,j,我们一定能给出对应的(i*j)的一个引子 x*j\y;
然后我们单独考虑都是质数的幂的情况,由此就可以得出来 d(ij)=(1+a1+b1)(1+a2+b2)...(1+an+bn)也就是所有相对应的互质的xy的个数(因为每一个都可以和其他所有搭配,而幂次可以从0到an)
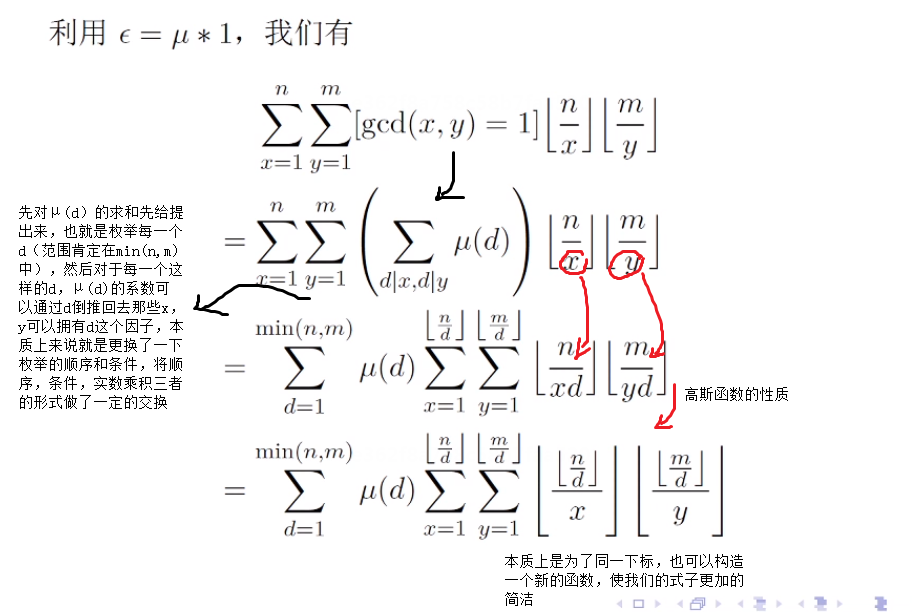

题意:
首先,我们给出一个结论: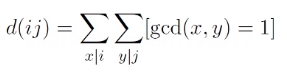
证明如下:1.对于给出的每一组互质的i,j,我们一定能给出对应的(i*j)的一个引子 x*j\y;
然后我们单独考虑都是质数的幂的情况,由此就可以得出来 d(ij)=(1+a1+b1)(1+a2+b2)...(1+an+bn)也就是所有相对应的互质的xy的个数(因为每一个都可以和其他所有搭配,而幂次可以从0到an)


