浅谈静态树链问题
开始前先进行一个全民投票吧!
投票:遇到静态树链问题,你会选择(点击选项进行投票):
1、直接树链剖分!
2、其他在线算法?
3、考虑离线算法。
4、本蒟蒻不会……
简介
本文主要讨论静态的树链问题。树链问题,可以看作树上的区间问题,这个区间可以看作一个结点 \(u\) 到另一个结点 \(v\) 所经最短路径形成的序列。这种问题大多需要用树链剖分来解决,但树链剖分会在解决对应区间问题的数据结构上增加一个 \(\log\),这无疑会大大增加算法的常数压力,因此本文将在静态树链问题上讨论其他解法。
由于作者能力有限,因此仅提供了三道例题,而且知道的解法并不多,因此本文的代码量十分饱满,理论方面的讲解对新人比较不友好,也希望大家能够提出其他高效的思路和建议。
例题一:树链求和
解法一:树链剖分
思路非常简单,就是纯粹的树链剖分,由于没有修改操作,可以直接跑前缀和,然后以 \(O(1)\) 的复杂度完成每次子区间查询,单次查询的时间复杂度为 \(O(\log n)\)。
这种做法的时间复杂度主要看查询的数据结构,在遇到复杂的静态树链问题上并不吃香,很容易被卡常。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int c[N] , a[N];
int sz[N] , w[N] , top[N] , dfn[N] , dfm[N] , dep[N] , fa[N], vis;
void dfsw(int u,int father) { //求重链
sz[u] = 1;
dep[u] = dep[father] + 1;
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
dfsw(v , u);
sz[u] += sz[v];
if(sz[v] > sz[w[u]]) w[u] = v;
}
}
void dfs(int u , int ftop) { //树链剖分
dfn[u] = ++vis , dfm[vis] = u , top[u] = ftop;
if(w[u]) dfs(w[u] , ftop);
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
if(v == w[u]) continue;
dfs(v , v);
}
}
int query(int x , int y) { //查询
int ans = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x , y);
ans += c[dfn[x]] - c[dfn[top[x]] - 1]; //统计子区间和
x = fa[top[x]];
}
if(dfn[x] < dfn[y]) swap(x , y);
ans += c[dfn[x]] - c[dfn[y] - 1];
I_love_Foccarus ans;
}
signed main() {
int n , root;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i]);
if(fa[i] != i)eadd(fa[i] , i);
else root = i;
}
dfsw(root , 0);
dfs(root , 0);
rep(i , 1 , n)c[i] = c[i - 1] + a[dfm[i]]; //前缀和初始化
int q;
in(q);
while(q--){
int u , v;
in(u) , in(v);
printf("%d\n",query(u , v));
}
I_love_Foccarus 0;
}
解法二:容斥原理(树上差分)
不难发现,查询的内容可减,因此可以先通过一轮 dfs 求出每个结点到根结点的路径形成的序列的序列和,用一个数组 \(f\) 储存下来。
然后举个例子,如图,查询 \(3,5\):
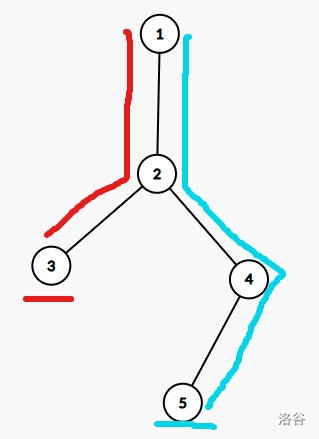
不难发现 \(f_{\operatorname{LCA}(u,v)}\) 被计算了两次,需要减去,然而 \(\operatorname{LCA}(u,v)\) 也在查询的树链内,因此还需将 \(\operatorname{LCA}(u,v)\) 的权值加上,从而得出结点 \(u\) 到结点 \(v\) 所经最短路径形成的序列的序列和为 \(f_u+f_v- 2f_{\operatorname{LCA}(u,v)}+a_{\operatorname{LCA}(u,v)}\),其中 \(a\) 表示点权。
而 \(a_{\operatorname{LCA}(u,v)}\) 又可以由 \(f_{\operatorname{LCA}(u,v)}-f_{fa_{\operatorname{LCA}(u,v)}}\) 得出,其中 \(fa\) 表示该结点的父亲结点。因此也可以写作 \(f_u+f_v- f_{\operatorname{LCA}(u,v)}-f_{fa_{\operatorname{LCA}(u,v)}}\),特殊的,如果 \(\operatorname{LCA}(u,v)\) 为根结点,那么查询的值就应为 \(f_u+f_v- f_{\operatorname{LCA}(u,v)}\),因为根结点没有父亲结点。
这种做法需要求 LCA,因此单次查询的时间复杂度同样为 \(O(\log n)\)。
虽然这种思路很简单,代码也很好写,但是处理的问题必须满足可减,这就是它的局限性。面对复杂的静态树链问题,这种做法往往不会被采用。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int n , q;
int fa[N][21] , d[N] , f[N];
void dfs(int u,int dep) { //倍增 LCA 初始化
d[u] = dep;
for(int i = head[u] ; i ; i = edge[i].nex){
int v = edge[i].act;
f[v] += f[u]; //记录该结点到根结点的权值和
dfs(v , dep + 1);
}
}
int LCA(int x , int y) { //倍增 LCA
if(d[x] < d[y])swap(x , y);
for(int i = 20 ; i >= 0 ; i--) {
int v = fa[x][i];
if(d[v] < d[y])continue;
x = v;
}
if(x == y)return x;
for(int i = 20 ; i >= 0 ; i--) {
if(fa[x][i] == fa[y][i])continue;
x = fa[x][i];
y = fa[y][i];
}
I_love_Foccarus fa[x][0];
}
signed main() {
int root;
in(n);
rep(i , 1 , n)in(f[i]);
rep(i , 1 , n) {
in(fa[i][0]);
if(fa[i][0] != i)eadd(fa[i][0] , i);
else root = i , fa[i][0] = 0; //让根结点指向权值为零的数
}
dfs(root , 1);
for(int i = 1 ; i <= 20 ; i++) { //倍增 LCA 初始化
for(int j = 1 ; j <= n ; j++) {
int v = fa[j][i - 1];
fa[j][i] = fa[v][i - 1];
}
}
in(q);
while(q--){
int u , v;
in(u) , in(v);
int lca = LCA(u , v);
printf("%d\n",f[u] + f[v] - f[lca] - f[fa[lca][0]]); //容斥原理求解
}
I_love_Foccarus 0;
}
解法三:Tarjan
类似于 Tarjan 离线求 LCA,但与之不同的是,我们需要用带权并查集进行维护。这种带权并查集的权值合并比较特殊,每个结点的权值不会加到父结点那里去,而是与之相反,将父结点的权值加到自身,这里可以看作权值合并的逆操作,而且这种合并可以路径压缩。注意这种操作不应将根结点的权值合并,因为每次查询都一定会重复合并到其根结点,因此最好的办法就是在路径压缩时不合并根结点,然后在处理答案时再分类讨论。
接下来来讨论处理答案。
处理答案需要满足查询的两个结点都已经与其 LCA 合并,因此需要枚举它们的 LCA,可以通过 Tarjan 离线求出 LCA,然后打下标记,在回溯到对应 LCA 时再进行处理。
由于查询的两个结点存在三种情况,现进行分类讨论。
设查询的两个结点为 \(u,v\),那么有以下情况:
\(u=v\):答案就为其 LCA 的点权。
\(\operatorname{LCA}(u,v)=u\) 或 \(\operatorname{LCA}(u,v)=v\):答案计算了 LCA 的点权,可以直接合并。
\(\operatorname{LCA}(u,v)\ne u\) 且 \(\operatorname{LCA}(u,v)\ne v\):答案没有计算 LCA 的点权,需要在合并答案时加上 LCA 的点权。
这种离线算法的时间复杂度严格意义上来讲是 \(O(q\log n)\),其中 \(n\) 表示结点数,\(q\) 表示查询次数。
这种离线算法的思想很通用,只要问题满足可合并,就可以使用该算法解决,而且效率较高,可以从下面的例题二中得以体现。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5 , maxn = 1e6 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
vector< pair< pair<int , int> , int > >solve[maxn]; //LCA 标记
vector< pair<int , int> >Q[maxn]; //离线储存查询
int n , q , fa[N] , vis[N] , d[N] , a[N] , ans[maxn];
int find(int x) { //带权并查集合并
if(fa[x] != fa[fa[x]]){ //如果父亲结点不是根结点
int root = find(fa[x]);
d[x] += d[fa[x]]; //将父亲结点权值合并到自身
fa[x] = root; //路径压缩
}
I_love_Foccarus fa[x];
}
void Tarjan(int u) { //Tarjan 离线求树链和
fa[u] = u , vis[u] = 1 , d[u] = a[u]; //结点初始化
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
Tarjan(v);
fa[v] = u; //可以直接合并
}
for(auto v:Q[u]){ //求 LCA 和打标记
if(!vis[v.fi])continue;
solve[find(v.fi)].push_back(make_pair(make_pair(u , v.fi) , v.se));
}
for(auto v:solve[u]){ //处理每次询问
find(v.fi.fi) , find(v.fi.se); //进行权值合并
if(v.fi.fi == v.fi.se) ans[v.se] = a[u]; //分类讨论
else if(v.fi.fi == u || v.fi.se == u ) ans[v.se] = d[v.fi.fi] + d[v.fi.se];
else ans[v.se] = d[v.fi.fi] + d[v.fi.se] + a[u];
}
}
signed main() {
int root;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
int f;
in(f);
if(f != i)eadd(f , i);
else root = i;
}
in(q);
rep(i , 1 , q) { //离线记录每次询问
int u , v;
in(u) , in(v);
Q[u].push_back(make_pair(v , i));
Q[v].push_back(make_pair(u , i));
}
Tarjan(root); //Tarjan 离线求树链和
rep(i , 1 , q) printf("%d\n",ans[i]);
I_love_Foccarus 0;
}
解法四:树上倍增
就像求倍增 LCA,在记录成倍增长的父结点信息的同时合并权值,然后在倍增求 LCA 的过程中将权值合并,也就是把查询的要合并的两条链拆解成若干个二进制片段,然后合并。信息不可重复,需要去重,为了权值避免权值重复合并,合并记录的信息不能计入成倍跳到了的结点的权值,然后在查询时加上漏掉的 LCA 的点权。
时间复杂度为 \(O(q\log n)\)。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int n , q;
int fa[N][21] , f[N][21] , d[N] , vis[N] , a[N];
void dfs(int u,int dep) { //树上倍增初始化
d[u] = dep;
for(int i = head[u] ; i ; i = edge[i].nex){
int v = edge[i].act;
dfs(v , dep + 1);
}
}
int root;
int solve(int x , int y) { //树上倍增
int ans = 0;
if(d[x] < d[y])swap(x , y);
for(int i = 20 ; i >= 0 ; i--) {
int v = fa[x][i];
if(d[v] < d[y])continue;
if(x != y)
ans += f[x][i];
x = v;
}
if(x == y) I_love_Foccarus ans + a[y];
for(int i = 20 ; i >= 0 ; i--) {
if(fa[x][i] == fa[y][i])continue;
ans += f[x][i] + f[y][i];
x = fa[x][i];
y = fa[y][i];
}
I_love_Foccarus ans + f[x][0] + f[y][0] + a[fa[x][0]];
}
signed main() {
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i][0]);
f[i][0] = a[i];
if(fa[i][0] != i)eadd(fa[i][0] , i);
else root = i;
}
dfs(root , 1);
for(int i = 1 ; i <= 20 ; i++) { //树上倍增初始化
for(int j = 1 ; j <= n ; j++) {
int v = fa[j][i - 1];
if(fa[j][i - 1] == fa[v][i - 1])continue; //去重
fa[j][i] = fa[v][i - 1];
f[j][i] = f[j][i - 1] + f[v][i - 1]; //权值合并
}
}
in(q);
while(q--){
int u , v;
in(u) , in(v);
printf("%d\n",solve(u , v));
}
I_love_Foccarus 0;
}
例题二:静态树链最大子段和
解法一:树链剖分
处理最大树链子段和,需要区间查询,而且该信息不可减,因此如果用线段树解决,最终还需将所有子区间合并,思路复杂且繁琐。而且单次查询的时间复杂度是 \(O(\log^2n)\),无法通过本题。
在处理结点往上跳的过程中处理两个结点到其 LCA 的链的合并信息,最后统一合并,与其链最大子段和与合并结果取最大值,合并结果为两个链的最大前缀和之和。注意区间的左边界是靠向根结点的,因为是按 dfs 序进行的树链剖分。至于如何合并,可参考解法三。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct node {
int a , b , c , d;
node() {
}
node(int x) {
this->a = this->b = this->c = this->d = x;
}
node friend operator + (const node &u , const node &v) { //重载加法处理合并
node ans;
ans.a = max(max(u.a , v.a) , v.c + u.d);
ans.b = u.b + v.b;
ans.c = max(u.c , u.b + v.c);
ans.d = max(v.d , v.b + u.d);
I_love_Foccarus ans;
}
};
struct linetree { //线段树
int cl , cr;
node ans;
};
vector<linetree>t;
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int sz[N] , w[N] , top[N] , dfn[N] , dfm[N] , dep[N] , fa[N], vis , a[N];
void dfsw(int u,int father) { //求重链
sz[u] = 1;
dep[u] = dep[father] + 1;
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
dfsw(v , u);
sz[u] += sz[v];
if(sz[v] > sz[w[u]]) w[u] = v;
}
}
void dfs(int u , int ftop) { //树链剖分
dfn[u] = ++vis , dfm[vis] = u , top[u] = ftop;
if(w[u]) dfs(w[u] , ftop);
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
if(v == w[u]) continue;
dfs(v , v);
}
}
int n , rt;
int build(int l , int r) { //建树
linetree tmp;
if(l == r) {
tmp.cl = tmp.cr = -1 , tmp.ans = node(a[dfm[l]]);
t.push_back(tmp);
I_love_Foccarus t.size() - 1;
}
int mid = (l + r) >> 1;
tmp.cl = build(l , mid) , tmp.cr = build(mid + 1 , r);
tmp.ans = t[tmp.cl].ans + t[tmp.cr].ans;
t.push_back(tmp);
I_love_Foccarus t.size() - 1;
}
node qry(int l , int r , int ql , int qr , int idx) { //子区间查询
if(r < ql || qr < l) {
node tmp = node(-0x3f3f3f3f);
tmp.b = 0;
I_love_Foccarus tmp;
}
if(ql <= l && r <= qr) {
I_love_Foccarus t[idx].ans;
}
int mid = (l + r) >> 1;
node x = qry(l , mid , ql , qr , t[idx].cl) , y = qry(mid + 1 , r , ql , qr , t[idx].cr);
I_love_Foccarus x + y ;
}
int query(int x , int y) { //查询
node ansx = node(-0x3f3f3f3f) , ansy = node(-0x3f3f3f3f); //分别处理两个结点到 LCA 的链的信息
ansx.b = ansy.b = 0;
while(top[x] != top[y]) {
if(dep[top[x]] >= dep[top[y]]) {
ansx = qry(1 , n , dfn[top[x]] , dfn[x] , rt) + ansx;
x = fa[top[x]];
} else {
ansy = qry(1 , n , dfn[top[y]] , dfn[y] , rt) + ansy;
y = fa[top[y]];
}
}
if(dfn[x] < dfn[y]) ansy = qry(1 , n , dfn[x] , dfn[y] , rt) + ansy;
else ansx = qry(1 , n , dfn[y] , dfn[x] , rt) + ansx;
I_love_Foccarus max(max(ansx.a , ansy.a) , ansx.c + ansy.c); //合并
}
signed main() {
int root;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i]);
if(fa[i] != i)eadd(fa[i] , i);
else root = i;
}
dfsw(root , 0);
dfs(root , 0);
rt = build(1 , n); //建树
int q;
in(q);
while(q--) {
int u , v;
in(u) , in(v);
printf("%d\n",query(u , v));
}
I_love_Foccarus 0;
}
解法二:猫树分治
树链剖分的时间主要浪费在线段树的查询上,可以在这方面进行优化。由于查询的是一个静态区间,因此考虑用猫树分治实现,至于如何合并,可参考解法三。
由于树链剖分需要查询 \(O(\log n)\) 个子区间,因此猫树需要处理 \(O(q\log n)\) 次查询,如果采用朴素的猫树,时间复杂度为 \(O(q\log^2 n)\),不能接受。猫树的一只 \(\log\) 主要消耗在确定 mid 上,可以在此方面进行优化。据说有一种二进制的方法可以直接实现,但是蒟蒻不会,因此用了 ST 表,维护区间内的一个数 \(x\),满足以 \(x\) 为 mid 的最大区间长度,可以证明,查询的区间一定处于该区间的内部。该算法常数稍大,但把优化打满后勉强能过。
总时间复杂度为 \(O(q\log n)\)。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct node {
int a , b , c , d;
node() {
}
node(int x) {
this->a = this->b = this->c = this->d = x;
}
node friend operator + (const node &u , const node &v) { //重载加法处理合并
node ans;
ans.a = max(max(u.a , v.a) , v.c + u.d);
ans.b = u.b + v.b;
ans.c = max(u.c , u.b + v.c);
ans.d = max(v.d , v.b + u.d);
I_love_Foccarus ans;
}
};
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
inline void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int sz[N] , w[N] , top[N] , dfn[N] , dfm[N] , dep[N] , fa[N], vis , a[N];
inline void dfsw(int u,int father) { //求重链
sz[u] = 1;
dep[u] = dep[father] + 1;
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
dfsw(v , u);
sz[u] += sz[v];
if(sz[v] > sz[w[u]]) w[u] = v;
}
}
inline void dfs(int u , int ftop) { //树链剖分
dfn[u] = ++vis , dfm[vis] = u , top[u] = ftop;
if(w[u]) dfs(w[u] , ftop);
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
if(v == w[u]) continue;
dfs(v , v);
}
}
int n;
int st[18][N] , pos[N] , lg[N] , dap[N];
node c[18][N];
inline int gets(int x , int y) { //求区间长度最长的 mid
I_love_Foccarus pos[x] > pos[y] ? x : y;
}
inline int find(int l , int r) { //ST 表查询
int logs = lg[r - l + 1];
I_love_Foccarus gets(st[logs][l] , st[logs][r - (1 << logs) + 1]);
}
inline void build(int l , int r , int d) { //构建猫树
if(l == r) I_love_Foccarus;
int mid = (l + r) >> 1;
if(pos[mid] < r - l + 1) { //ST 表处理的信息初始化
pos[mid] = r - l + 1; //记录 mid 能够表示的最大区间长度
dap[mid] = d; //记录深度
}
c[d][mid] = node(a[dfm[mid]]);
for(int i = mid - 1 ; i >= l ; i--)
c[d][i] = node(a[dfm[i]]) + c[d][i + 1];
c[d][mid + 1] = node(a[dfm[mid + 1]]);
for(int i = mid + 2 ; i <= r ; i++)
c[d][i] = c[d][i - 1] + node(a[dfm[i]]);
build(l , mid , d + 1) , build(mid + 1 , r , d + 1);
}
inline node qry(int l , int r) { //子区间查询
if(l == r) I_love_Foccarus node(a[dfm[l]]);
int mid = (find(l,r)) , d = dap[find(l,r)];
if(l <= mid && mid < r) I_love_Foccarus c[d][l] + c[d][r];
else if(r == mid) I_love_Foccarus c[d][l];
else I_love_Foccarus c[d][r];
}
inline int query(int x , int y) { //查询
node ansx = node(-0x3f3f3f3f) , ansy = node(-0x3f3f3f3f); //分别处理两个结点到 LCA 的链的信息
ansx.b = ansy.b = 0;
while(top[x] != top[y]) {
if(dep[top[x]] >= dep[top[y]]) {
ansx = qry(dfn[top[x]] , dfn[x]) + ansx;
x = fa[top[x]];
} else {
ansy = qry(dfn[top[y]] , dfn[y]) + ansy;
y = fa[top[y]];
}
}
if(dfn[x] < dfn[y]) ansy = qry(dfn[x] , dfn[y]) + ansy;
else ansx = qry(dfn[y] , dfn[x]) + ansx;
I_love_Foccarus max(max(ansx.a , ansy.a) , ansx.c + ansy.c); //合并
}
signed main() {
int root;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i]);
if(fa[i] != i)eadd(fa[i] , i);
else root = i;
}
dfsw(root , 0);
dfs(root , 0);
build(1 , n , 1);
for(int i = 2 ; i <= n ; i++) lg[i] = lg[i >> 1] + 1;
for(int i = 1 ; i <= n ; i++) st[0][i] = i;
for(int i = 1 ; i <= lg[n] ; i++) { //ST 表初始化
for(int j = 1 ; j <= n - (1 << (i - 1)) + 1 ; j++) {
st[i][j] = gets(st[i - 1][j] , st[i - 1][j + (1 << (i - 1))]);
}
}
int q;
in(q);
while(q--) {
int u , v;
in(u) , in(v);
printf("%d\n",query(u , v));
}
I_love_Foccarus 0;
}
解法三:Tarjan
不难发现,最大子段和满足可合并,因此可以通过上述的 Tarjan 方法进行维护,用带权并查集维护四个信息,分别为最大子段和、树链和、最大前缀和、最大后缀和,方便合并。
接下来讨论合并。
为了方便,我们用 \(a,b,c,d\) 分别来表示最大子段和、树链和、最大前缀和、最大后缀和,\(u,v\) 表示合并的左右两个信息,\(f\) 表示合并后的信息。
1、最大子段和合并:
有三种情况,如图:
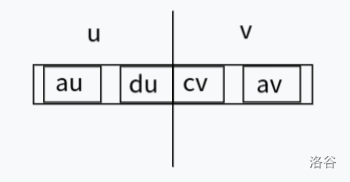
对这三种情况取最大值就是合并后的最大子段和,查询时的合并是将最大后缀和合并,分类讨论判断是否需要同 LCA 一同合并,如果需要,可将两个最大后缀和与 \(0\) 取最大值,因为 LCA 可以选择不之合并。
2、树链和合并:
直接将两个树链和相加即可。
3、最大前缀和合并:
有两种情况,第一种最大前缀和就是 \(c_u\),第二种是 \(b_u+c_v\),然后对两种情况取最大值。
4、最大后缀和合并:
同最大前缀和合并一样,有两种情况,第一种是 \(d_v\),第二种是 \(b_v+d_u\),对两种情况取最大值即可。
综上可以得出:
\(a_f=\max(c_v+d_u,a_u,a_v),b_f=b_u+b_v,c_f=\max(c_u,b_u+c_v),d_f=\max(d_v,b_v+d_u)\)。
那么这道题也就很好做了,按上述合并方法处理权值合并,合并的复杂度是 \(O(1)\) 级别的,因此时间复杂度依旧是 \(O(q\log n)\),可以通过。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5 , maxn = 3e6 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
struct node{
int a , b , c , d;
node() {
}
node(int x) {
this->a = this->b = this->c = this->d = x;
}
node friend operator + (const node &u , const node &v) { //重载加法处理合并
node ans;
ans.a = max(max(u.a , v.a) , v.c + u.d);
ans.b = u.b + v.b;
ans.c = max(u.c , u.b + v.c);
ans.d = max(v.d , v.b + u.d);
I_love_Foccarus ans;
}
}d[N];
vector< pair< pair<int , int> , int > >solve[maxn]; //LCA 标记
vector< pair<int , int> >Q[maxn]; //离线储存查询
int n , q , fa[N] , vis[N] , a[N] , ans[maxn];
int find(int x) { //带权并查集合并
if(fa[x] != fa[fa[x]]){ //如果父亲结点不是根结点
int root = find(fa[x]);
d[x] = d[x] + d[fa[x]]; //将父亲结点权值合并到自身
fa[x] = root; //路径压缩
}
I_love_Foccarus fa[x];
}
int c(int x){ //与 0 取 max
I_love_Foccarus x > 0 ? x : 0;
}
void Tarjan(int u) { //Tarjan 离线求树链最大子段和
fa[u] = u , vis[u] = 1 , d[u] = node(a[u]); //结点初始化
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
Tarjan(v);
fa[v] = u; //可以直接合并
}
for(auto v:Q[u]){ //求 LCA 和打标记
if(!vis[v.fi])continue;
solve[find(v.fi)].push_back(make_pair(make_pair(u , v.fi) , v.se));
}
for(auto v:solve[u]){ //处理每次询问
find(v.fi.fi) , find(v.fi.se); //进行权值合并
if(v.fi.fi == v.fi.se) ans[v.se] = a[u]; //分类讨论
else if(v.fi.fi == u){
ans[v.se] = max(max(d[v.fi.fi].a , d[v.fi.se].a) , d[v.fi.fi].d + d[v.fi.se].d);
} else {
ans[v.se] = max(max(d[v.fi.fi].a , d[v.fi.se].a) , c(d[v.fi.fi].d) + c(d[v.fi.se].d) + a[u]);
}
}
}
signed main() {
int root;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
int f;
in(f);
if(f != i)eadd(f , i);
else root = i;
}
in(q);
rep(i , 1 , q) { //离线记录每次询问
int u , v;
in(u) , in(v);
Q[u].push_back(make_pair(v , i));
Q[v].push_back(make_pair(u , i));
}
Tarjan(root);
rep(i , 1 , q) printf("%d\n",ans[i]);
I_love_Foccarus 0;
}
解法四:树上倍增
和例题一的思路一样,合并操作用加法重载后根本不用改,只需在返回值时分类讨论即可。时间复杂度一样。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
I_love_Foccarus x*f;
}
struct node{
int a , b , c , d;
node() {
}
node(int x) {
this->a = this->b = this->c = this->d = x;
}
node friend operator + (const node &u , const node &v) { //重载加法处理合并
node ans;
ans.a = max(max(u.a , v.a) , v.c + u.d);
ans.b = u.b + v.b;
ans.c = max(u.c , u.b + v.c);
ans.d = max(v.d , v.b + u.d);
I_love_Foccarus ans;
}
}f[N][21];
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
inline void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int n , q;
int fa[N][21] , d[N] , vis[N] , a[N];
void dfs(int u,int dep) { //树上倍增初始化
d[u] = dep;
for(int i = head[u] ; i ; i = edge[i].nex){
int v = edge[i].act;
dfs(v , dep + 1);
}
}
int root;
inline int c(int x){
return x > 0 ? x : 0;
}
int solve(int x , int y) { //树上倍增
node ansx = node(-0x3f3f3f3f) , ansy = node(-0x3f3f3f3f); //分别处理两个结点到 LCA 的链的信息
ansx.b = ansy.b = 0;
if(d[x] < d[y])swap(x , y);
for(int i = 20 ; i >= 0 ; i--) {
int v = fa[x][i];
if(d[v] < d[y])continue;
if(x != y)
ansx = ansx + f[x][i];
x = v;
}
if(x == y) I_love_Foccarus max(max(ansx.a , a[y]) , ansx.d + a[y]);
for(int i = 20 ; i >= 0 ; i--) {
if(fa[x][i] == fa[y][i])continue;
ansx = ansx + f[x][i];
ansy = ansy + f[y][i];
x = fa[x][i];
y = fa[y][i];
}
ansx = ansx + f[x][0];
ansy = ansy + f[y][0];
I_love_Foccarus max(max(ansx.a , ansy.a) , c(ansx.d) + c(ansy.d) + a[fa[x][0]]);
}
signed main() {
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i][0]);
f[i][0] = node(a[i]);
if(fa[i][0] != i)eadd(fa[i][0] , i);
else root = i;
}
dfs(root , 1);
for(int i = 1 ; i <= 20 ; i++) { //树上倍增初始化
for(int j = 1 ; j <= n ; j++) {
int v = fa[j][i - 1];
if(fa[j][i - 1] == fa[v][i - 1])continue; //去重
fa[j][i] = fa[v][i - 1];
f[j][i] = f[j][i - 1] + f[v][i - 1]; //权值合并
}
}
in(q);
while(q--){
int u , v;
in(u) , in(v);
printf("%d\n",solve(u , v));
}
I_love_Foccarus 0;
}
例题三:静态树链点权第 \(k\) 小
具体思路:容斥原理(树上差分)
可以发现,该题合并的复杂度较高,因此一些依赖于合并的算法被成功 hack 掉。不难发现信息可减,因此可以考虑容斥,通过遍历一遍树建立可持久化线段树,也就是通过动态开点求出每个结点到根结点的路径形成的序列的权值树合并后的结果,然后再用例题一提到的式子进行权值树合并和查询即可。
参考代码如下:
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define I_love_Foccarus return
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define deap(i,a,b) for(int i=a;i>=b;i--)
#define in(a) a=read()
#define fi first
#define se second
const int N = 1e5 + 5;
const int inf = INT_MAX;
inline int read() { //浓缩后的快读
int x=0,f=1,ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct Edge { //链式前向星存树
int act , nex;
} edge[N];
int head[N] , eid;
void eadd(int u , int v) {
edge[++eid].act = v , edge[eid].nex = head[u] , head[u] = eid;
}
int n , q;
int a[N] , b[N] , tot;
int sz[N] , w[N] , top[N] , dfn[N] , dfm[N] , dep[N] , fa[N], vis;
void dfsw(int u,int father) { //求重链
sz[u] = 1;
dep[u] = dep[father] + 1;
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
dfsw(v , u);
sz[u] += sz[v];
if(sz[v] > sz[w[u]]) w[u] = v;
}
}
void dfs(int u , int ftop) { //树链剖分
dfn[u] = ++vis , dfm[vis] = u , top[u] = ftop;
if(w[u]) dfs(w[u] , ftop);
for(int i = head[u] ; i ; i = edge[i].nex) {
int v = edge[i].act;
if(v == w[u]) continue;
dfs(v , v);
}
}
int LCA(int x , int y) { //树剖求 LCA
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x , y);
x = fa[top[x]];
}
I_love_Foccarus dep[x] < dep[y] ? x : y;
}
struct linetree{
int cl , cr , ans;
};
int rt[N];
vector<linetree> tree;
int change(int idx , int l , int r , int q , int val){ //修改
linetree tmp = tree[idx];
if(l == r){
tmp.ans += val;
tree.push_back(tmp);
I_love_Foccarus tree.size() - 1;
}
int mid = (l + r) >> 1;
if(q <= mid) tmp.cl = change(tmp.cl , l , mid , q , val);
else tmp.cr = change(tmp.cr , mid + 1 , r , q , val);
tmp.ans = tree[tmp.cl].ans + tree[tmp.cr].ans;
tree.push_back(tmp);
I_love_Foccarus tree.size() - 1;
}
int query(int idxu , int idxv , int lca , int lca2 , int l , int r , int q){ //查询
if(l == r) I_love_Foccarus l;
int mid = (l + r) >> 1 , tmp = tree[tree[idxu].cl].ans + tree[tree[idxv].cl].ans - tree[tree[lca].cl].ans - tree[tree[lca2].cl].ans; //容斥原理求解
if(q <= tmp) I_love_Foccarus query(tree[idxu].cl , tree[idxv].cl , tree[lca].cl , tree[lca2].cl , l , mid , q);
else I_love_Foccarus query(tree[idxu].cr , tree[idxv].cr , tree[lca].cr , tree[lca2].cr , mid + 1 , r , q - tmp);
}
void build(int u){ //建树
for(int i = head[u] ; i ; i = edge[i].nex){
int v = edge[i].act;
a[v] = lower_bound(b + 1 , b + tot + 1 , a[v]) - b;
rt[v] = change(rt[u] , 1 , tot , a[v] , 1);
build(v);
}
}
signed main() {
//fast();
int root = 0;
in(n);
rep(i , 1 , n)in(a[i]);
rep(i , 1 , n) {
in(fa[i]);
b[i] = a[i];
if(fa[i] != i)eadd(fa[i] , i);
else eadd(0 , i) , fa[i] = 0;
}
sort(b + 1 , b + n + 1);
tot = unique(b + 1 , b + n + 1) - b - 1;
linetree tmp;
tmp.cl = tmp.cr = tmp.ans = 0;
tree.push_back(tmp);//建立初始根结点
dfsw(root , 0);
dfs(root , 0);
build(root);
in(q);
while(q--){
int u , v , k;
in(u) , in(v) , in(k);
int lca = LCA(u , v);
printf("%d\n",b[query(rt[u] , rt[v] , rt[lca] , rt[fa[lca]] , 1 , tot , k)]); //权值树查询
}
I_love_Foccarus 0;
}
参考
梦熊云智计划教练提供的抽象的思路。
我自己曾经的清朝代码。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号