tarjan学习报告
今天来讲讲 tarjan。
tarjan 的实例包括但不限于缩点、割边、割点。
首先说说 tarjan 在干什么。我们记录一个 dfn 序,dfn 表示时间戳。然后维护一个 low 数组,low 的定义是从 \(x\) 出发所能到的最小的 dfn 的值,那么我们对于一个回到 dfn 更小的点时,我们令 \(low[x]=min(low[x],dfn[v])\),然后对于 \(x\) 的祖先节点我们 \(low[u]=min(low[u],low[v])\) 即可。
而对于割点,定义就是删掉这个点后整个图不是连通图,即连通块个数 \(\ge 2\)。怎么求呢?我们还是借助 tarjan,我们发现,对于一个节点 \(u\),若他存在一个儿子节点 \(v\),使得 \(dfn[u]>=low[v]\),也就是说这个点的所有子节点没有回到 \(u\) 之前的祖先,那么我们就发现 \(u\) 是一个割点,而两个割点之间的边自然就是割边了。
tarjan 的用处是什么呢?
- 可以缩点后
dp。对于一个有环的图,这个图就会存在dp的后效性,怎么消除呢?缩点,如果无向图就跑树上dp,否则就拓扑跑dp。 - 对于割边,我们会有一些好玩的计数好题。
讲完了,可以看例题了。
P4645 [COCI 2006/2007 #3] BICIKLI
跑 tarjan,判断是否存在强连通分量。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5,MOD=1e9;
int low[N],dfn[N],T,n,m,in[N],s[N],tp,S[N],de[N],f[N],cnt,sz[N],vis[N],VIS[N];
vector<int> G[N],G1[N];
queue<int> q;
void dfs(int x)
{
vis[x]=1;
for(int v:G[x])
{
de[v]++;
if(vis[v]) continue;
dfs(v);
}
}
void DFS(int x)
{
VIS[x]=1;
for(int v:G1[x])
{
if(VIS[v]) continue;
DFS(v);
}
}
void tarjan(int x)
{
dfn[x]=low[x]=++T;
in[x]=1,s[++tp]=x;
for(int v:G[x])
{
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(in[v])
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
while(true)
{
int u=s[tp];tp--;
in[u]=0,S[u]=cnt,sz[cnt]++;
if(u==x) break;
}
}
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].push_back(v);
G1[v].push_back(u);
}
dfs(1),DFS(2);
if(!vis[2]) {cout<<0;return 0;}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++)
if(vis[i]&&VIS[i]&&sz[S[i]]>=2)
{
cout<<"inf";
return 0;
}
q.push(1),f[1]=1;
while(!q.empty())
{
int x=q.front();q.pop();
for(int v:G[x])
{
if(!vis[v]) continue;
f[v]=(f[v]+f[x])%MOD;
if(!--de[v]) q.push(v);
}
}
cout<<f[2];
return 0;
}
P3119 [USACO15JAN] Grass Cownoisseur G
记住这个套路:一条边有往返走的次数的上界时,首先想到分层图。
我们 tarjan 后缩点建双层图跑最长路即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
const int N = 2e5 + 5;
vector<int> Adj[N], E[N];
int dfn[N], low[N], T, sz[N], S[N], cnt, vis[N], dp[N];
bool inst[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++T;
inst[u] = true;
s.push(u);
for (auto v : Adj[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (inst[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++cnt;
while (true) {
int h = s.top();
s.pop();
sz[cnt]++;
S[h] = cnt;
inst[h] = false;
if (h == u) break;
}
}
}
queue<int> q;
void spfa() {
memset(vis, 0, sizeof(vis));
vis[S[1]] = 1;
q.push(S[1]);
while (!q.empty()) {
int h = q.front();
q.pop();
vis[h] = 0;
for (auto v : E[h]) {
if (dp[v] < dp[h] + sz[h]) {
dp[v] = dp[h] + sz[h];
if (!vis[v]) vis[v] = 1, q.push(v);
}
}
}
}
signed main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
Adj[u].push_back(v);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= cnt; i++) sz[i + cnt] = sz[i];
if (cnt == 1) {
cout << sz[1] << endl;
return 0;
}
for (int i = 1; i <= n; i++) {
for (auto j : Adj[i]) {
if (S[i] == S[j]) continue;
E[S[i]].push_back(S[j]);
E[S[j]].push_back(S[i] + cnt);
E[S[i] + cnt].push_back(S[j] + cnt);
}
}
spfa();
cout << dp[S[1] + cnt] << endl;
return 0;
}
P5008 [yLOI2018] 锦鲤抄
这道题首先明白一个点。这道题一定是跟拓扑序有关的。我们对图缩点,然后就出现了一个 DAG,那么这个时候,我们只有一种点没法被删掉:在一个强连通分量里权值是最小的且这个强连通分量缩完点是入度为 \(0\) 的。
这个还是比较显而易见的。在一个强连通分量里,我们每一次删掉一个点就会少一个点,直到最后剩下一个没有入度的点。
那么除了这些无法选到的点,其他的点都能选到吗?肯定可以,我们任选能选择的点,然后按照拓扑序删掉即可。而我们为了答案最大,我们选那些可以选择且权值前 \(k\) 大的点。
注意有自环。
#include<bits/stdc++.h>
#define pii pair<int,int>
#define pib pair<int,bool>
#define pll pair<ll,ll>
#define fi first
#define se second
#define pb push_back
#define ep emplace_back
using namespace std;
const int N=2e6+5;
int n,m,k,dfn[N],low[N],T,st[N],tp,cnt,id[N],S[N];
vector<int> G[N];
bool in[N];
pib a[N];
void tarjan(int x)
{
dfn[x]=low[x]=++T;
in[x]=true,st[++tp]=x;
for(int v:G[x])
{
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(in[x])
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
int mn=1e9,sz=0,pos;
while(true)
{
int u=st[tp];
tp--,sz++,in[u]=false,S[u]=cnt;
if(mn>a[u].fi)
mn=a[u].fi,pos=u;
if(u==x) break;
}
if(sz>1) id[cnt]=pos;
}
}
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
cin>>a[i].fi;
a[i].se=false;
}
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].pb(v),a[v].se=true;
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
memset(in,false,sizeof(in));
for(int i=1;i<=n;i++)
for(int j:G[i])
if(i==j) in[S[i]]=true;
else if(S[i]!=S[j]) in[S[j]]=true;
for(int i=1;i<=cnt;i++)
if(!in[i]) a[id[i]].se=false;
sort(a+1,a+1+n,greater<pib>());
int ans=0;
for(int i=1;i<=n;i++)
if(a[i].se)
{
ans+=a[i].fi;
k--;
if(!k) break;
}
cout<<ans;
return 0;
}
P2783 有机化学之神偶尔会做作弊
听说以前是黑题????这都能黑????
一眼缩点然后倍增 LCA 啊。
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int dfn[N],m,low[N],T,f[N][15],in[N],cnt,n,st[N],tp,S[N],dep[N];
vector<int> G[N],E[N];
map<int,int> F[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-') f=-1;ch=getchar();}
while(ch<='9'&&ch>='0') x=(x<<1)+(x<<3)+(ch^'0'),ch=getchar();
return x*f;
}
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++T;
in[x]=1,st[++tp]=x;
for(int v:G[x])
{
if(v==fa) continue;
if(!dfn[v])
{
tarjan(v,x);
low[x]=min(low[x],low[v]);
}
else if(in[v])
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
while(true)
{
int u=st[tp];tp--;
S[u]=cnt,in[u]=0;
if(u==x) break;
}
}
}
void dfs(int x,int fa)
{
f[x][0]=fa,dep[x]=dep[fa]+1;
for(int i=1;i<=14;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int v:E[x])
{
if(v==fa) continue;
dfs(v,x);
}
}
int LCA(int x,int y)
{
if(dep[x]<dep[y])
swap(x,y);
for(int i=14;~i;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=14;~i;i--)
{
if(f[x][i]==f[y][i]) continue;
x=f[x][i],y=f[y][i];
}
return f[x][0];
}
inline void print(int x)
{
if(x==0)return putchar('0'),void();
if(x==1)return putchar('1'),void();
print(x>>1),putchar((x&1)+'0');
}
signed main()
{
n=read(),m=read();
for(int i=1;i<=m;i++)
{
int u,v;u=read(),v=read();
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
for(int u=1;u<=n;u++)
for(int v:G[u])
{
if(S[u]==S[v]||F[S[u]][S[v]]) continue;
F[S[u]][S[v]]=F[S[v]][S[u]]=1;
E[S[u]].push_back(S[v]);
E[S[v]].push_back(S[u]);
}
dfs(S[1],0);
cin>>m;
while(m--)
{
int x=S[read()],y=S[read()];
print(dep[x]+dep[y]-dep[LCA(x,y)]*2+1);
printf("\n");
}
return 0;
}
P2403 [SDOI2010] 所驼门王的宝藏
这道题绝对好题。
暴力做法就是 \(RL\) 建边,时空复杂度均为 \(\mathcal O(RL)\),估计用一台超型计算机就可以跑完吧。
考虑优化见图。我们发现有很多的边都是浪费的。因为实际上用到的边并不是很多。
我们考虑先建立 \(R\) 个点,表示有 \(R\) 行,每一行的连通块缩为一个点,再建立 \(L\) 个点,表示 \(L\) 列,这个是同理的。再建立 \(n\) 个特殊点,一共有 \(R+L+n\) 个点。
然后我们考虑怎么加边。首先对于前两个操作是很容易的,第三个操作 map 存一下即可。如果追求小常数可以选择二分。
然后就是常规的去 tarjan 就行了。
注意,这道题卡常。
总时间复杂度 \(\mathcal O(n\log n+T)\)。其中 \(T=n+R+L\)。
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2.1e6+5,M=1e5+5,TT=1e6+5;
const int dx[8]={1,1,1,0,0,-1,-1,-1};
const int dy[8]={1,0,-1,1,-1,1,0,-1};
int n,r,c,dfn[N],low[N],T,st[N],tp,S[N],cnt,sz[N],de[N],f[N];
int h[N],ne[TT],t[TT],cnt1,cnt2;
bool in[N];
pii E[TT];
queue<int> q;
struct node
{
int x,y,t;
bool operator<(const node &A) const
{
if(x!=A.x) return x<A.x;
return y<A.y;
}
}a[M];
inline void add1(int u,int v)
{
ne[++cnt1]=h[u];
t[cnt1]=v;
h[u]=cnt1;
E[cnt1]={u,v};
}
inline void add2(int u,int v)
{
ne[++cnt2]=h[u];
t[cnt2]=v;
h[u]=cnt2;
}
inline int getid(int x, int y)
{
int l=1,r=n;
while(l<=r)
{
int mid=(l+r)>>1;
if(a[mid].x==x&&a[mid].y==y) return mid;
else if(a[mid].x<x||(a[mid].x==x&&a[mid].y<y)) l=mid+1;
else r=mid-1;
}
return -1;
}
inline void tarjan(int x)
{
dfn[x]=low[x]=++T;
st[++tp]=x,in[x]=true;
for(int i=h[x];~i;i=ne[i])
{
int v=t[i];
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(in[v])
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
while(true)
{
int u=st[tp];tp--;
in[u]=false,S[u]=cnt,sz[cnt]+=(u>r+c);
if(u==x) break;
}
}
}
int main()
{
memset(h,-1,sizeof(h));
scanf("%d%d%d",&n,&r,&c);
for(int i=1;i<=n;i++)
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].t);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
{
auto [x,y,t]=a[i];
add1(x,r+c+i),add1(r+y,r+c+i);
if(t==1) add1(r+c+i,x);
else if(t==2) add1(r+c+i,r+y);
else
{
for(int j=0;j<8;j++)
{
int xx=x+dx[j],yy=y+dy[j];
if(xx<1||xx>r||yy<1||yy>c) continue;
int id=getid(xx,yy);
if(~id) add1(r+c+i,r+c+id);
}
}
}
n=r+c+n;
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
memset(h,-1,sizeof(h));
for(int i=1;i<=cnt1;i++)
{
if(S[E[i].fi]==S[E[i].se]) continue;
add2(S[E[i].fi],S[E[i].se]),de[S[E[i].se]]++;
}
for(int i=1;i<=cnt;i++)
if(!de[i]) q.push(i),f[i]=sz[i];
while(!q.empty())
{
int x=q.front();
q.pop();
for(int j=h[x];~j;j=ne[j])
{
int v=t[j];
f[v]=max(f[v],f[x]+sz[v]);
if(!--de[v]) q.push(v);
}
}
int mx=0;
for(int i=1;i<=cnt;i++)
mx=max(mx,f[i]);
printf("%d",mx);
return 0;
}
P2746 [USACO5.3] 校园网Network of Schools
这道题先用 tarjan 缩点,然后对于第一行,我们只需要输出现在的图上入度为 \(0\) 的点,第二行输出入度为 \(0\) 的个数与 出度为 \(0\) 的个数的较大值。
#include <bits/stdc++.h>
using namespace std;
int n;
const int N = 1005;
vector<int> adj[N];
int dfn[N], low[N], TIME;
stack<int> st;
bool inst[N];
int cnt;
int scc[N], sz[N];
bool flag[N][N];
int in[N], out[N];
void tarjan(int u) {
dfn[u] = low[u] = ++TIME;
inst[u] = true;
st.push(u);
for (auto v : adj[u]) {
if (dfn[v] == 0) {
tarjan(v);
low[u] = min(low[v], low[u]);
} else if (inst[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
++cnt;
while (true) {
int v = st.top();
st.pop();
inst[v] = false;
scc[v] = cnt;
sz[cnt]++;
if (u == v) {
break;
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
int u;
while (cin >> u) {
if (u == 0) {
break;
}
adj[i].push_back(u);
}
}
for (int i = 1; i <= n; ++i) {
if (dfn[i] == 0) {
tarjan(i);
}
}
for (int i = 1; i <= n; ++i) {
for (auto v : adj[i]) {
if (scc[i] != scc[v] && !flag[scc[i]][scc[v]]) {
flag[scc[i]][scc[v]] = 1;
in[scc[v]]++;
out[scc[i]]++;
}
}
}
int A, B;
A = B = 0;
for (int i = 1; i <= cnt; ++i) {
if (in[i] == 0) {
A++;
}
if (out[i] == 0) {
B++;
}
}
cout << A << endl;
for (int i = 1; i <= cnt; ++i) {
if (sz[cnt] == n) {
cout << 0 << endl;
return 0;
}
}
cout << max(A, B) << endl;
return 0;
}
P4782 【模板】2-SAT
来讲一讲 tarjan 的一个延伸物:2-SAT。
2-SAT 能解决这个问题:我们对于两个点 \(x\) 和 \(y\),然后我们有若干个要求就是若 \(a\) 则 \(b\),若非 \(a\) 则非 \(b\)。
对于这种情况,我们可以这么做。假设我们 \(a\) 是真,那么 \(b\) 就是真的,我们就 \(a\rightarrow b\);如果 \(a\) 是假的,那么 \(b\) 就是假的,即 \(-a\rightarrow -b\)。
然后我们取跑 tarjan,如果我们发现 \(a\) 与 \(-a\) 出现在同一个强连通分量里,我们就发现无解,否则有解。
说白了,如果出现如果这个就必然有那个的描述,一般都用 2-SAT。
对于这道模板题,我们可以这么思考。\(x_i\) 为 \(a\) 或 \(x_j\) 为 \(b\)。如果 \(x_i\neq a\),那么肯定有 \(x_j = b\),我们就 \(-i\rightarrow j\);反之如果 \(x_j\neq b\),那么就一定有 \(x_i=a\),即 \(-j\rightarrow i\)。然后跑 2-SAT 判断即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 4e6 + 5;
int n, m, T, cnt_edge, s;
int dfn[N], low[N], S[N], head[N];
bool inst[N];
stack<int> st;
struct node {
int to, nxt;
}Adj[N];
void add_edge(int u, int v) {
Adj[++cnt_edge].nxt = head[u];
Adj[cnt_edge].to = v;
head[u] = cnt_edge;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++T;
st.push(u);
inst[u] = true;
for (int i = head[u]; ~i; i = Adj[i].nxt) {
int v = Adj[i].to;
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else if(inst[v]) low[u] = min(low[u], dfn[v]);
}
if(dfn[u] == low[u]) {
s++;
while(true) {
int h = st.top();
st.pop();
S[h] = s;
inst[h] = false;
if (h == u) break;
}
}
}
int main() {
cin >> m >> n;
memset(head, -1, sizeof(head));
for (int i = 1; i <= n; i++) {
char c1, c2;
int a, b, x, y;
cin >> a >> x >> b >> y;
c1 = (x == 1 ? '+' : '-');
c2 = (y == 1 ? '+' : '-');
if (c1 == '-' && c2 == '-') {
add_edge(a + m, b);
add_edge(b + m, a);
} else if (c1 == '-' && c2 == '+') {
add_edge(a + m, b + m);
add_edge(b, a);
} else if (c1 == '+' && c2 == '-') {
add_edge(a, b);
add_edge(b + m, a + m);
} else if (c1 == '+' && c2 == '+') {
add_edge(a, b + m);
add_edge(b, a + m);
}
}
for (int i = 1; i <= (m << 1); i++)
if(!dfn[i]) tarjan(i);
for (int i = 1; i <= m; i++) {
if(S[i] == S[i + m]) {
printf("IMPOSSIBLE\n");
return 0;
}
}
printf("POSSIBLE\n");
for(int i = 1; i <= m; i++) {
if(S[i] > S[i + m]) printf("1 ");
else printf("0 ");
}
puts("");
return 0;
}
P4652 [CEOI 2017] One-Way Streets
这道题被某一个D类大佬秒了/bx。
首先缩点,一个强连通分量里的边全都是无法定向的。
我们考虑其他的边如何定向。我们用差分的思想,对于 \(u\) 和 \(v\),设 \(u\) 到 LCA 的路径上标记为 \(-1\),而从 LCA 到 \(v\) 的路径上标记为 \(1\)。然后我们考虑怎么求出答案。
我们考虑树上差分。我们计算以 \(u\) 为根的子树之和,如果是 \(<0\) 的那就是 \(R\),否则就是 \(L\)。
但是由于我们 dfs 的时候无法确定什么时候是正的什么时候是反的。所以我们 dfs 的时候要加上一个 op 表示我是走的逆过程还是顺过程,那么最后也就是要判断 \(pre[x]*op\) 的正负了。
#include<bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
const int N=1e5+5;
int dfn[N],low[N],T,n,m,in[N],cnt,bel[N],sz[N];
vector<pii> G[N],E[N];
map<int,bool> F[N];
stack<int> ST;
char ans[N];
void tarjan(int x,int I)
{
dfn[x]=low[x]=++T;
ST.push(x),in[x]=1;
for(auto [v,id]:G[x])
{
if(id==-I) continue;
if(!dfn[v])
{
tarjan(v,id);
low[x]=min(low[x],low[v]);
}
else if(in[v])
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
cnt++;
while(true)
{
int u=ST.top();ST.pop();
in[u]=0,bel[u]=cnt;
if(u==x) break;
}
}
}
void dfs(int x,int I,int op)
{
dfn[x]=1;
for(auto [v,id]:E[x])
{
if(dfn[v]) continue;
if(id>0) dfs(v,abs(id),1);
else dfs(v,abs(id),-1);
sz[x]+=sz[v];
}
if(sz[x]*op>0) ans[I]='L';
else if(sz[x]*op<0) ans[I]='R';
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].emplace_back(v,i);
G[v].emplace_back(u,-i);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,-1);
for(int i=1;i<=n;i++)
for(auto [j,id]:G[i])
{
if(bel[i]==bel[j]) continue;
E[bel[i]].emplace_back(bel[j],id);
}
int k;cin>>k;
while(k--)
{
int u,v;cin>>u>>v;
sz[bel[u]]++,sz[bel[v]]--;
}
memset(dfn,0,sizeof(dfn));
for(int i=1;i<=m;i++) ans[i]='B';
for(int i=1;i<=n;i++)
if(!dfn[i])
dfs(i,0,0);
for(int i=1;i<=m;i++)
cout<<ans[i];
return 0;
}
P5025 [SNOI2017] 炸弹
昨日下午三点多钟,线段树优化先生到了重庆。线段树优化先生来了!数据结构听了高兴,图论听了高兴,所有算法听了都高兴,无疑问的,大家都认为这是OI的一大喜事。---《OI报》
这道题是大家最喜欢的线段树优化建图。
首先考虑最暴力的做法。我们求出一个炸弹能炸到的区间,然后两两建边跑 tarjan 缩点,然后将一个连通块内的区间的左右端点更新出来,统计答案。
这样的做法是 \(\mathcal O(n^2)\) 的。接下来考虑换一台超级计算机。
我们考虑用线段树优化建图,这样就是 \(\mathcal O(n\log n)\) 的。线段树优化见图显然之前提到过。
#include<bits/stdc++.h>
#define fi first
#define se second
#define int long long
#define pii pair<int,int>
using namespace std;
const int N=5e5+5,MOD=1e9+7;
pii a[N<<2];
vector<int> G[N<<2],E[N<<2];
int n,x[N<<2],r[N<<2],id[N<<2],tot;
int dfn[N<<2],low[N<<2],cnt,TIME,s[N<<2],top,b[N<<2];
int vis[N<<2],LL[N<<2],RR[N<<2],ans;
bool inst[N<<2];
void tarjan(int x)
{
dfn[x]=low[x]=++TIME;
s[++top]=x,inst[x]=true;
for(int v:G[x])
{
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(inst[v]) low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
++cnt;
while(true)
{
int u=s[top];top--;
inst[u]=false;
b[u]=cnt;
LL[cnt]=min(LL[cnt],a[u].fi);
RR[cnt]=max(RR[cnt],a[u].se);
if(u==x) break;
}
}
}
void build(int x,int l,int r)
{
a[x]={l,r},tot=max(tot,x);
if(l==r)
{
id[l]=x;
return ;
}
int mid=(l+r)>>1;
build(x<<1,l,mid),build(x<<1|1,mid+1,r);
G[x].push_back(x<<1),G[x].push_back(x<<1|1);
}
void link(int x,int l,int r,int ql,int qr,int v)
{
if(ql<=l&&r<=qr)
{
if(v!=x) G[v].push_back(x);
return ;
}
int mid=(l+r)>>1;
if(ql<=mid) link(x<<1,l,mid,ql,qr,v);
if(qr>mid) link(x<<1|1,mid+1,r,ql,qr,v);
}
void dfs(int x)
{
vis[x]=1;
for(int v:E[x])
{
if(vis[v])
{
LL[x]=min(LL[x],LL[v]);
RR[x]=max(RR[x],RR[v]);
continue;
}
dfs(v);
LL[x]=min(LL[x],LL[v]);
RR[x]=max(RR[x],RR[v]);
}
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>x[i]>>r[i];
build(1,1,n);
x[n+1]=1e18;
for(int i=1;i<=n;i++)
{
if(!r[i]) continue;
int L=lower_bound(x+1,x+1+n,x[i]-r[i])-x;
int R=upper_bound(x+1,x+1+n,x[i]+r[i])-x-1;
link(1,1,n,L,R,id[i]);
a[id[i]]={L,R};
}
memset(LL,0x3f,sizeof(LL));
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
for(int i=1;i<=tot;i++)
for(int j:G[i])
{
if(b[i]==b[j]) continue;
E[b[i]].push_back(b[j]);
}
for(int i=1;i<=cnt;i++)
{
sort(E[i].begin(),E[i].end());
unique(E[i].begin(),E[i].end());
}
for(int i=1;i<=cnt;i++)
if(!vis[i]) dfs(i);
for(int i=1;i<=n;i++)
{
int x=RR[b[id[i]]]-LL[b[id[i]]]+1;
ans=(ans+i*x%MOD)%MOD;
}
cout<<ans<<endl;
return 0;
}
圆方树
下面来讲讲割点与桥所诞生的延伸物---圆方树。
众所周知,我们对于一些无向有环图,我们是可以缩点跑树的。但是有的时候缩点并不优秀。原因是缩点后对于强连通分量内部的操作会比较复杂。所以我们引入 圆方树。
先来说说圆方树的建造过程。我们将同一个点双内的点连向同一个虚点,去掉点双内除了向虚点连边的其他边。
过程如下。
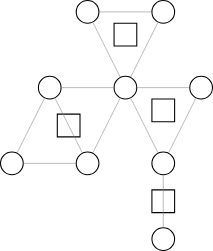
可以看出,圆方树只会存在圆圆点和园方点。
这样就克服了缩点后不保留内部点的信息的缺点。
如果只想保存圆方点,我们只需要把 \(low[v]==dfn[x]\) 改为 \(low[v]>=dfn[x]\) 即可。
可以看看代码的实现。
void tarjan(int s)
{
low[s]=dfn[s]=++cnt;
st[++top]=s;
for(int v:G[s])
{
if(!dfn[v])
{
tarjan(v);
low[s]=min(low[s],low[v]);
if(low[v]==dfn[s])
{
num++;
for(int x=0;x!=v;top--)
{
x=st[top];
G2[x].push_back(num);
G2[num].push_back(x);
}
G2[s].push_back(num);
G2[num].push_back(s);
}
}
else
low[s]=min(low[s],dfn[v]);
}
}
有人说他就是愚忠与缩点,那我会让你改变想法的。
P3388 【模板】割点(割顶)
咕咕咕咕。
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5;
int n,m,dfn[N],low[N],T,is[N],vis[N];
vector<int> G[N];
void tarjan(int x,int y)
{
dfn[x]=low[x]=++T;
int cnt=0;
for(int v:G[x])
{
if(v==y) continue;
if(!dfn[v])
{
cnt++;
tarjan(v,x);
low[x]=min(low[x],low[v]);
if(x!=y&&low[v]>=dfn[x])
is[x]=1;
}
else low[x]=min(low[x],dfn[v]);
}
if(cnt>=2&&x==y) is[x]=1;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
int ans=0;
for(int i=1;i<=n;i++)
if(is[i]) ans++;
cout<<ans<<"\n";
for(int i=1;i<=n;i++)
if(is[i]) cout<<i<<" ";
return 0;
}
P3469 [POI 2008] BLO-Blockade
之前提到过,有割点就有可能考计数。他来了他来了。
我们先考虑非割点。对于非割点,答案显然为 \(2(n-1)\),考虑割点的答案。
我们按照 tarjan 的顺序,记录一下切除这个点后,剩余的各连通块大小。然后进行计数即可。计数的方法类似于树,不展开讨论。\
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,m,dfn[N],low[N],T,sz[N],ans[N],is[N];
vector<int> G[N];
void tarjan(int x,int y)
{
dfn[x]=low[x]=++T,sz[x]=1;
int cnt=0,sum=0;
for(int v:G[x])
{
if(v==y) continue;
if(!dfn[v])
{
tarjan(v,x);
sz[x]+=sz[v];
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])
{
ans[x]+=sz[v]*(n-sz[v]);
cnt++,sum+=sz[v];
if(x!=1||cnt>1) is[x]=1;
}
}
else low[x]=min(low[x],dfn[v]);
}
if(!is[x]) ans[x]=2*(n-1);
else ans[x]+=n-1+(n-sum-1)*(sum+1);
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
tarjan(1,1);
for(int i=1;i<=n;i++)
cout<<ans[i]<<"\n";
return 0;
}
P4320 道路相遇
这道题就是找从 \(u\) 到 \(v\) 上有多少割点。这道题圆方树巨简单无比,那些要缩点的,我写了1k圆方树,2k缩点,是不是有点思想改变?
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=5e5+5;
vector<int> G[N<<1],G2[N<<1];
int dfn[N<<1],cnt,low[N<<1],num;
int tp[N<<1],dep[N<<1],fa[N<<1],sz[N<<1],hson[N<<1];
int st[N<<1],top;
void tarjan(int s)
{
low[s]=dfn[s]=++cnt;
st[++top]=s;
for(int v:G[s])
{
if(!dfn[v])
{
tarjan(v);
low[s]=min(low[s],low[v]);
if(low[v]==dfn[s])
{
num++;
for(int x=0;x!=v;top--)
{
x=st[top];
G2[x].push_back(num);
G2[num].push_back(x);
}
G2[s].push_back(num);
G2[num].push_back(s);
}
}
else
low[s]=min(low[s],dfn[v]);
}
}
void dfs1(int x,int f)
{
dep[x]=dep[f]+1;
fa[x]=f;
sz[x]=1,hson[x]=-1;
for(int v:G2[x])
{
if(v==fa[x])
continue;
dfs1(v,x);
sz[x]+=sz[v];
if(hson[x]==-1||sz[v]>sz[hson[x]])
hson[x]=v;
}
}
void dfs2(int x,int t)
{
tp[x]=t;
if(hson[x]==-1)
return;
dfs2(hson[x],t);
for(int v:G2[x])
{
if(v==fa[x]||v==hson[x])
continue;
dfs2(v,v);
}
}
int LCA(int x,int y)
{
while(tp[x]!=tp[y])
{
if(dep[tp[x]]<dep[tp[y]])
swap(x,y);
x=fa[tp[x]];
}
if(dep[x]>dep[y])
swap(x,y);
return x;
}
int main()
{
cin>>n>>m;
num=n;
for(int i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i),top--;
cnt=0;
dfs1(1,0);
dfs2(1,1);
int q;
cin>>q;
while(q--)
{
int u,v;
cin>>u>>v;
cout<<((dep[u]+dep[v]-(dep[LCA(u,v)]<<1))>>1)+1<<endl;
}
return 0;
}
P4630 [APIO2018] 铁人两项
一眼圆方树吧。首先建出圆方树,然后枚举中转点 \(c\)。发现对于一个点,他的贡献是与上面这道题的计数方法类似的。这里我们发现一件事。对于全是圆方边的树,那就是圆点会被重复算一次。所以我们要减掉圆点的权值贡献。
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define pib pair<int,bool>
#define pll pair<ll,ll>
#define fi first
#define se second
#define pb push_back
#define ep emplace_back
using namespace std;
const int N=2e5+5;
int a[N],n,m,cnt,T,dfn[N],low[N],s[N],tp,w[N],sz[N],ans;
vector<int> G[N],E[N];
void tj(int x)
{
dfn[x]=low[x]=++T,w[x]=-1,s[++tp]=x;
for(int v:G[x])
{
if(!dfn[v])
{
tj(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])
{
cnt++;
while(true)
{
int u=s[tp];tp--;
E[cnt].pb(u),E[u].pb(cnt),w[cnt]++;
if(u==v) break;
}
E[cnt].pb(x),E[x].pb(cnt),w[cnt]++;
}
}
else low[x]=min(low[x],dfn[v]);
}
}
void dfs(int x,int y)
{
sz[x]=(x<=n);
for(int v:E[x])
{
if(v==y) continue;
dfs(v,x);
ans+=2*sz[x]*sz[v]*w[x];
sz[x]+=sz[v];
}
ans+=2*sz[x]*(T-sz[x])*w[x];
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].pb(v),G[v].pb(u);
}
cnt=n;
for(int i=1;i<=n;i++)
if(!dfn[i])
{
tp=T=0;
tj(i),dfs(i,0);
}
cout<<ans;
return 0;
}
P3225 [HNOI2012] 矿场搭建
这道题也是一个分类好题。我们考虑从一个点去找他能找到的割点。首先考虑找不到割点,我们要建立两个救援出口。如果一个找到了一个割点,即这是一个叶子连通块,我们就只需要建立一个救援站,建在叶子节点即可。如果找到两个及以上的割点,我们就不需要救援站。因为我们无论割哪一个点,我们都能走到叶子上。毕竟这个 \(V\) 保证联通嘛。
#include<bits/stdc++.h>
#define int long long
#define pb push_back
#define ep emplace_back
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
int dfn[505],low[505],vis[505];
bool cut[505];
int n,m,cnt,num,TI,ans1,T,C,ans2;
vector<int> G[505];
void clear()
{
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(cut,0,sizeof(cut));
memset(vis,0,sizeof(vis));
cnt=TI=n=ans1=T=0,ans2=1;
}
void tarjan(int x,int y)
{
dfn[x]=low[x]=++TI;
int sz=0;
for(int v:G[x])
if(!dfn[v])
{
sz++;
tarjan(v,x);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]&&x!=y)
cut[x]=true;
}
else if(v!=y) low[x]=min(low[x],dfn[v]);
if(x==y&&sz>=2) cut[x]=true;
}
void dfs(int x)
{
vis[x]=T;
if(cut[x]) return;
cnt++;
for(int v:G[x])
{
if(cut[v]&&vis[v]!=T) num++,vis[v]=T;
if(!vis[v]) dfs(v);
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
while(cin>>m&&m)
{
clear();
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
n=max(n,max(u,v));
G[u].pb(v),G[v].pb(u);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
for (int i=1;i<=n;i++)
if (!vis[i]&&!cut[i])
{
T++,cnt=num=0;
dfs(i);
if (!num) ans1+=2,ans2*=cnt*(cnt-1)/2;
if (num==1) ans1++,ans2*=cnt;
}
cout<<"Case "<<(++C)<<": "<<ans1<<" "<<ans2<<"\n";
for(int i=1;i<=n;i++) G[i].clear();
}
return 0;
}
P5058 [ZJOI2004] 嗅探器
一句话题面:无向连通图中有A、B两点,问是否存在一个点能切断A、B之间的联系。
然后发现是圆方树。
#include <iostream>
#include <cstdio>
#include <vector>
#include <stack>
#include <cstdlib>
using namespace std;
const int MAXN = 400005;//这里注意要开双倍空间,因为圆方树上点的个数可能到2n的数量
//n是原图中点的数量,start和target是两个服务器,nn是圆方树上点的数量
int n, start, target, nn, pre[MAXN], low[MAXN], dt;
//分别是原图,和圆方树的邻接表
vector<int> adj[MAXN], adjT[MAXN];
stack<int> s;
void tarjan(int u, int father) {
pre[u] = low[u] = ++dt;
s.push(u);
for (int i = 0; i < adj[u].size(); ++i) {
int v = adj[u][i];
if (pre[v] == 0) {
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= pre[u]) {
nn++;//找到一个新的点双连通分量,新增一个方点
while (true) {
int t = s.top();
s.pop();
adjT[nn].push_back(t);//原图中的点到方点连边
adjT[t].push_back(nn);
if (t == v) break;//这里pop到v为止,u点保留在栈里面,因为割点可能被很多点双公用
}
adjT[u].push_back(nn);//u点也在这个点双里面,也像方点连边。
adjT[nn].push_back(u);
}
} else if (v != father) {
low[u] = min(low[u], pre[v]);
}
}
}
//u是当前访问到的点,ans是目前从根走下来的路径上的答案,father是u的父亲
void dfs(int u, int ans, int father) {
if (u == target) {
//如果走到target了
if (ans == 0) {
//ans还是0,说明路上没经过割点
printf("No solution\n");
} else {
printf("%d\n", ans);
}
exit(0);
}
if (u != start && adjT[u].size() > 1 && u <= n) {
//遇到非叶子的圆点,说明是割点
if (ans == 0) {
ans = u;
} else {
ans = min(ans, u);
}
}
for (int i = 0; i < adjT[u].size(); ++i) {
int v = adjT[u][i];
if (v == father) continue;
dfs(v, ans, u);
}
}
int main() {
scanf("%d", &n);
int u, v;
while (scanf("%d%d", &u, &v)) {
if (u == 0 && v == 0) break;
adj[u].push_back(v);
adj[v].push_back(u);
}
scanf("%d%d", &start, &target);
nn = n;//最开始的时候,圆方树里面点的个数等于圆点个数
tarjan(start, 0);//从其中一个服务器开始跑一遍tarjan
if (pre[target] == 0) {
//从起点到终点不连通
printf("No solution\n");
return 0;
}
//这时候以start为根,在圆方树上dfs找target,沿途记录经过的最小的割点编号
dfs(start, 0, 0);
return 0;
}
P4606 [SDOI2018] 战略游戏
这道题强度有点大。
我们首先考虑建圆方树,然后暴力的做法就是去枚举 \(S\) 内的任意两个点,这样做法就是 \(\mathcal O(\sum |S|^2\log |S|)\),可以获得 \(75pts\)。
考虑更优秀做法。我们的瓶颈在于枚举子集内两个点。能不能不枚举呢?显然可以。我们容易发现,这些这些可以删掉的点一定在这些点所组成的虚树上。所以我们考虑建出虚树,然后答案就是虚树大小 \(-|S|\)。
#include<bits/stdc++.h>
#define int long long
// #define ll long long
#define pii pair<int,int>
#define pib pair<int,bool>
#define pll pair<ll,ll>
#define fi first
#define se second
#define pb push_back
#define ep emplace_back
using namespace std;
const int N=5e5+5;
int a[N],n,m,T,TI,dfn[N],low[N],s[N],tp,f[N][25],cnt,dep[N],DFN1[N],DFN2[N],TIM,stk[N],TP,dis[N],F[N];
vector<int> G[N],E[N];
void clear()
{
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(s,0,sizeof(s));
memset(f,0,sizeof(f));
memset(dis,0,sizeof(dis));
memset(dep,0,sizeof(dep));
memset(DFN1,0,sizeof(DFN1));
memset(DFN2,0,sizeof(DFN2));
memset(F,0,sizeof(F));
TI=tp=TP=TIM=0;
}
void tj(int x,int y)
{
dfn[x]=low[x]=++TI;
s[++tp]=x;
for(int v:G[x])
if(!dfn[v])
{
tj(v,x);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])
{
cnt++;
E[cnt].pb(x),E[x].pb(cnt),F[cnt]=x;
while(true)
{
int u=s[tp];tp--;
E[cnt].pb(u),E[u].pb(cnt),F[u]=cnt;
if(u==v) break;
}
}
}
else if(v!=y) low[x]=min(low[x],dfn[v]);
}
void dfs(int x,int fa)
{
f[x][0]=fa,dep[x]=dep[fa]+1,DFN1[x]=++TIM,dis[x]=dis[fa]+(x<=n);
for(int i=1;i<=18;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int v:E[x])
{
if(v==fa) continue;
dfs(v,x);
}
DFN2[x]=TIM;
}
int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=18;~i;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=18;~i;i--)
{
if(f[x][i]==f[y][i]) continue;
x=f[x][i],y=f[y][i];
}
return f[x][0];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>T;
while(T--)
{
clear();
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;cin>>u>>v;
G[u].pb(v),G[v].pb(u);
}
cnt=n;
for(int i=1;i<=n;i++)
if(!dfn[i]) tj(i,i);
dfs(1,1);
int q;cin>>q;
while(q--)
{
int ss;cin>>ss;
for(int i=1;i<=ss;i++)
cin>>a[i];
sort(a+1,a+1+ss,[&](int x,int y)
{
return DFN1[x]<DFN1[y];
});
int tot=ss;
for(int i=1;i<ss;i++)
a[++tot]=LCA(a[i],a[i+1]);
sort(a+1,a+1+tot),tot=unique(a+1,a+1+tot)-a-1;
sort(a+1,a+1+tot,[&](int x,int y)
{
return DFN1[x]<DFN1[y];
});
int ans=0;TP=0,stk[0]=F[a[1]];
for(int i=1;i<=tot;i++)
{
int x=a[i];
while(TP&&!(DFN1[stk[TP]]<DFN1[x]&&DFN2[stk[TP]]>=DFN2[x])) TP--;
ans+=dis[x]-dis[stk[TP]],stk[++TP]=x;
}
cout<<ans-ss<<"\n";
}
for(int i=1;i<=cnt;i++) G[i].clear(),E[i].clear();
}
return 0;
}
CF487E Tourists
这把缩点要完败了。
首先考虑圆方树,然后发现既有修改又有查询所以考虑树剖即可。时间复杂度为 \(\mathcal O(n\log n)\)。
试问那些要缩点的,你更改一个强连通分量内点的权值的时候,怎么更新整个强连通分量的值?还要对点开线段树吗?
代码难度太大,改天写完了补上…………(上一道虚树题已经把我搞疯了)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号