P5659 [CSP-S 2019] 树上的数 题解

P5659 [CSP-S 2019] 树上的数 题解

题意

Link

给定一棵树和每个节点上的初始数字，删除一条边的效果是交换被这条边连接的两个节点上的数字交换。

设 \(p_i\) 表示数字 \(i\) 在哪个节点，要求合理安排删除 \(n-1\) 条边的顺序，使得排列 \(p\) 字典序最小，

$n \leq 2000n≤2000 $

---

分析

对于这个十分友善（ 毒瘤 ）的 不可做 题，正解这种东西肯定不是正常人不能想出来的，于是我们先考虑暴力

Part1. \(n \leq 10\)

没脑子的傻暴力， 不解释

---

Part2. 菊花图

你看到数据范围中“ 存在度数为 \(n - 1\) 的节点”， 这使你 充满信心 有了非分之想 ：

首先来一张菊花图 ：

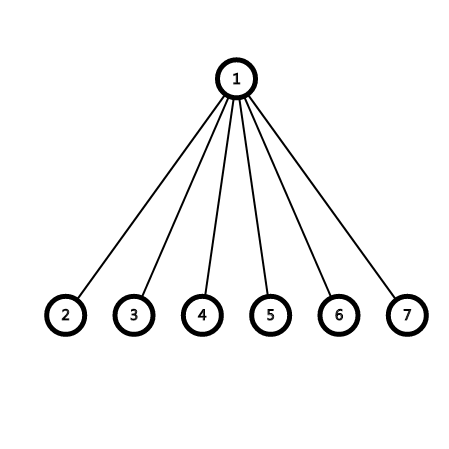
加入我们按顺序删除 1->2 的边， 1 ->3 的边， ……， 1 -> 7 的边。

你会惊奇的发现，点的移动变成了 1 -> 2, 2 -> 3, ……， 7 -> 1

他的移动其实就是把数字向后移了一位，所以我们可以得到一个简单的贪心策略 ：

先枚举点上的数字所在的点 ， 然后找下一个点 ， 在枚举的过程中我们维护一个边的并查集 ， 用来维护他是否已经被加入， 预计得分 \(25pts\)。

---

Part3. 链

你看到数据范围中 “树的形态是一条 链 ”， 这使你 充满信心 又有了非分之想，

咱再来一条链

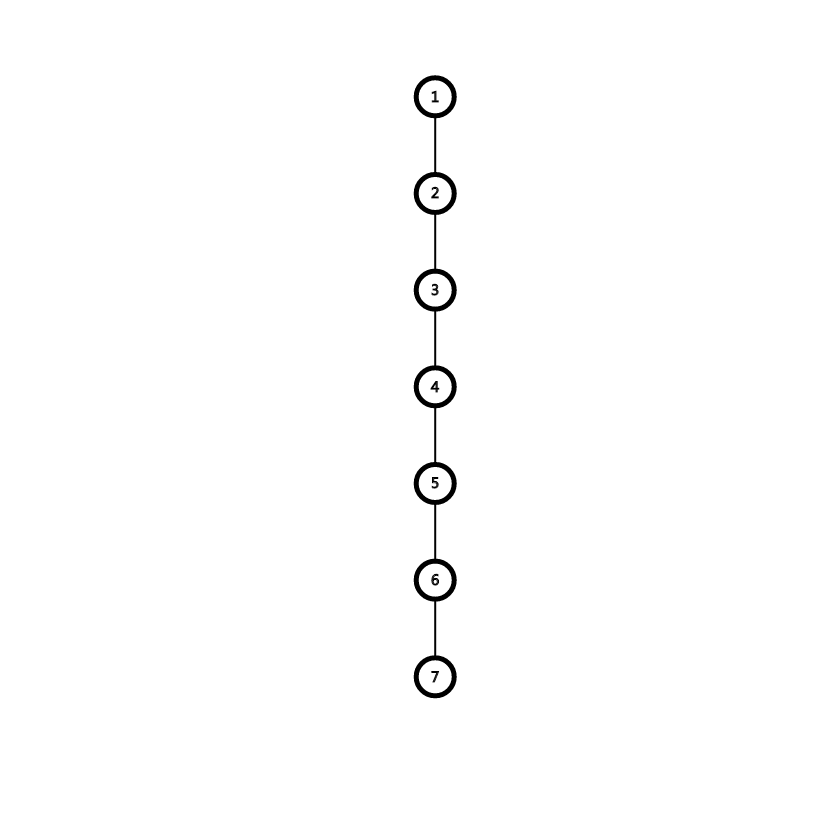
我们考虑一个点上的数字想到另一个点上需要考虑的东西 ：

如果节点 1 上的数字想到节点 2 ， 那我我必然先删掉边 1 -> 2 , 再删掉2 -> 3, 这就会是我们考虑另一个问题 :

删边的顺序问题 ，于是我们就又有了一个贪心策略 ：

1. 枚举每一个数字 ， 在合法的情况下找到字典序最小的点 ，作为这个节点的最终目标节点。
2. 当我们选定一个节点是我们一定会产生一系列先后条件的限制， 然后去维护（冰茶姬什么的乱搞就可以， 反正是骗分 ）

---

Part.fin 正解

首先整棵树

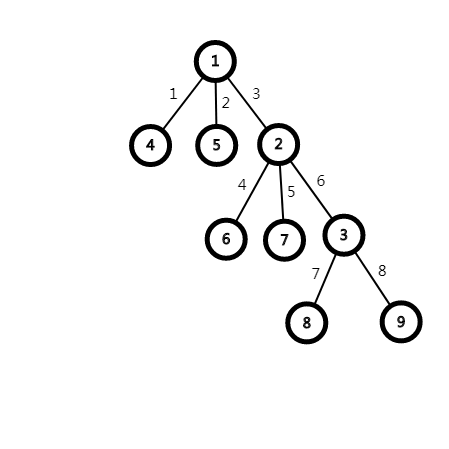
考虑我们 \(Part3\) 的乱搞，我们同样可以搞出一堆小的链，（就是出世界颠倒目标节点的链），然后我们在结合 \(Part2\) 的乱搞，我们可以发现，对于点到他的目标节点，我们有如下限制 （以节点1->节点3为例）：

1. \(3\) 号边必须是 \(1\) 号点的连边里优先级最高的。

2. \(6\) 号边必须是 \(3\) 号点连边中优先级最小的

3. \(6\) 号边的优先级必须紧挨着 \(3\) 号边的优先级
   ​于是我们就又可以用冰茶姬们维护连边了吼吼吼~

---

Part.EX 代码实现

#include<bits/stdc++.h>
//#define int long long
//#define rint register int
using namespace std;
const int maxn = 1e5 + 5,mod = 1e9 + 7;

namespace IOS {

	inline int read() {
	    char c=getchar(),f=0;int t=0;
	    for(;c<'0'||c>'9';c=getchar()) if(!(c^45)) f=1;
	    for(;c>='0'&&c<='9';c=getchar()) t=(t<<1)+(t<<3)+(c^48);
	    return f?-t:t;
	}

	inline __int128 read_() {
	    char c=getchar(),f=0;int t=0;
	    for(;c<'0'||c>'9';c=getchar()) if(!(c^45)) f=1;
	    for(;c>='0'&&c<='9';c=getchar()) t=(t<<1)+(t<<3)+(c^48);
	    return f?-t:t;
	}

	inline void write(int num) {
		if(num < 0) {
			putchar('-');
			num = -num;
		}
		if(num > 9) write(num / 10);
		putchar(num % 10 + '0');
	}

	inline void write_(__int128 num) {
		if(num < 0) {
			putchar('-');
			num = -num;
		}
		if(num > 9) write_(num / 10);
		putchar(num % 10 + '0');
	}

};

using namespace IOS;

int T, n, tot, fin;
int in[maxn], out[maxn], fa[maxn];
int siz[maxn];
int poi[maxn], du[maxn];
int ver[maxn * 5], nxt[maxn * 5], head[maxn];

inline void add(int x, int y) {
	ver[++tot] = y;
	nxt[tot] = head[x];
	head[x] = tot;
}

inline void allzero() {
	memset(head, 0, sizeof head);
	memset(du, 0, sizeof du);
	memset(in, 0, sizeof in);
	memset(out, 0, sizeof out);
	tot = 0;
}

inline int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}

inline bool judge(int x, int y, int li) {
	if(in[y] || out[x]) return false;
	int fx = find(x), fy = find(y);
	if(fx == fy && siz[fx] != li) return false;
	return true;
}

void dfs1(int now, int fro) {
	if(fro != now && judge(fro, now, du[now] + 1)) fin = min(fin, now); //检查合法性
	for(int i = head[now], y; i; i = nxt[i]) {
		y = ver[i];
		if(i == fro) continue;
		if(judge(fro, i, du[now] + 1)) {
			dfs1(y, i ^ 1);//^1表示这个变的反向边，便于处理
		}
	}
}

inline void merge(int x, int y) { // 啥子合并
//	合并的结果就是起点->一堆边->终点
	int fx = find(x), fy = find(y);
	fa[fx] = fy, siz[fy] += siz[fx];
	out[x] = in[y] = true;
}

bool dfs2(int x, int fro, int poi) { // 标记沿途的点 / 边
	if(x == poi) {
		merge(fro, fin);
		return true;
	}
	
	for(int i = head[x], y; i; i = nxt[i]) {
		y = ver[i];
		if(i == fro) continue;
		if(dfs2(y, i ^ 1, poi)) {
			merge(fro, i);
			return true;
		}
	}
	
	return false;
}

signed main() {
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	T = read();
	
	while(T--) {
		allzero(); // 初始化
		
		n = read();
		
		tot = (n + 1) / 2 * 2 + 1; // 我们给边建成虚点，方便冰茶姬
		// 这是在为点提供预留的空间
		
		for(int i = 1; i <= n; ++ i) poi[i] = read();
		
		for(int i = 1, u, v; i < n; ++ i) {
			u = read(), v = read();
			add(u, v), add(v, u);
			du[u] ++, du[v] ++;
		}
		
		for(int i = 1; i <= tot; ++ i) fa[i] = i, siz[i] = 1; // 并查集初始化
		
		for(int i = 1; i <= n; ++ i) {
			int x = poi[i];
			fin = n + 1; // 寻找最终节点（只要能到达那个地方）
			dfs1(x, x); // 开始寻找
			dfs2(x, x, fin); //一定要到达那个地方
			cout << fin << " ";
		}
		
		cout << endl;
	}
//	fclose(stdin);fclose(stdout);
}