Manacher&KMP算法
Manacher算法
Manacher模板
题目描述
给出一个只由小写英文字符 a,b,c,…y,z 组成的字符串 S ,求 S 中最长回文串的长度 。
字符串长度为 n。
输入格式
一行小写英文字符 a,b,c,⋯,y,z 组成的字符串 S。
输出格式
一个整数表示答案。
分析
1st. 一般性思路:对于给定的每一个字符s[i],都搜一遍 --> O(n^2)
2nd. 通过记忆划,将每一次求出的答案储存,再根据亿点点Manacher分析 --> O(n)
3rd. Manacher
- 加速过程

- 时间复杂度分析:
易证:c,r,len均只升不降,且r的变化与c,len相关,可以得到r变化的时间复杂度即为Manacher的时间复杂度 --> O(n)
代码
#include "bits/stdc++.h"
using namespace std;
const int N=1e7+5;
int n,l[5*N],ans=-1;
string a="#";
/*a[i]有:
它被中心位置为cr的回文子串包含;
回文半径右边界;
-> r一直++,直至r=n-1,时间复杂度为O(n)
以它为中心的回文子串半径为len;*/
void Manacher(){
int c=0,r=0,len=0;
for(int i=0;i<n;i++){
//如果在r以内,len直接=其以c的对称点的len';否则,最小为1
len= r>i?min(l[2*c-i],r-i):1;
//最普通的,直接while求回文半径len
while(i+len<n&&i-len>=0&&a[i+len]==a[i-len])
len++;
//如果半径超过了r,更新
if(i+len>r){
r=i+len;
c=i;
}
//存答案
l[i]=len;
ans=max(ans,len);
}
return ;
}
int main(){
char x;
while(cin>>x)a+=x,a+="#";
n=a.length();
Manacher();
cout<<ans-1;
return 0;
}
扩展KMP
洛谷:P5410【模板】扩展 KMP/exKMP(Z 函数)
题目描述
给定两个字符串 a,b,你要求出两个数组:
b 的 z 函数数组 z,即 b 与 b 的每一个后缀的 LCP 长度。
b 与 a 的每一个后缀的 LCP 长度数组 p。
对于一个长度为 n 的数组 a,设其权值为 xori=1ni×(ai+1)。
输入格式
两行两个字符串 a,b。
输出格式
第一行一个整数,表示 z 的权值。
第二行一个整数,表示 p 的权值。
分析
1st. 与Manacher类似,旦不是KMP!
2nd. 扩展KMP
-
z数组记字符串与其后缀的最长公共前缀长度。
-
e数组记最长可扩展后缀长度。
-
加速过程
![]()
-
时间复杂度分析:同Manacher -> O(n)
代码
#include "bits/stdc++.h"
#define ll long long
using namespace std;
const int N=2*1e7+5;
long long z[N],e[N],xz=0,xe=0;
string a,b;
void zArray(string a,int n){
z[0]=n;
ll c=1,r=1,len;
for(int i=1;i<n;i++){
len= r>i?min(r-i,z[i-c]):0;
while(i+len<n&&a[i+len]==a[len])
len++;
if(i+len>r){
r=i+len;
c=i;
}
z[i]=len;
}
return ;
}
void eArray(string a,string b,int n,int m){
ll c=0,r=0,len;
for(int i=0;i<n;i++){
len= r>i?min(r-i,z[i-c]):0;
while(i+len<n&&len<m&&a[i+len]==b[len])
len++;
if(i+len>r){
r=i+len;
c=i;
}
e[i]=len;
}
return ;
}
int main(){
cin>>a>>b;
zArray(b,b.length());
eArray(a,b,a.length(),b.length());
for(int i=0;i<b.length();i++)
xz^=(i+1)*(z[i]+1);
for(int i=0;i<a.length();i++)
xe^=(i+1)*(e[i]+1);
cout<<xz<<endl<<xe;
return 0;
}
KMP算法
题目描述
给出两个字符串 s1 和 s2,若 s1 的区间 [l,r] 子串与 s2 完全相同,则称 s2 在 s1 中出现了,其出现位置为 l。
现在请你求出 s2 在 s1 中所有出现的位置。
定义一个字符串 s 的 border 为 s 的一个非 s 本身的子串 t,满足 t 既是 s 的前缀,又是 s 的后缀。
对于 s2,你还需要求出对于其每个前缀 s′ 的最长 border t′ 的长度。
输入格式
第一行为一个字符串,即为 s1。
第二行为一个字符串,即为 s2。
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序输出 s2 在 s1 中出现的位置。
最后一行输出 ∣s2∣ 个整数,第 i 个整数表示 s2 的长度为 i 的前缀的最长 border 长度。
分析
1st. 参考Manacher,目标将时间复杂度:O(n*m) --> O(n+m)
2nd. KMP
- 首先求出next数组记模式字符串的前缀和后缀的最长公共元素长度 --> O(m)
- 加速过程(同Manacher) --> O(n)
(1) next数组跳跃过程:
I. 重点在每个点回溯上一个点的next值;
II. 以及判断该点与前缀的终止点的值是否相等。
(2) 匹配主流程:
I. 如果能对上,继续;
II. 如果对不上了,查找next数组达到移动模式字符串的目的。
3rd. by Deepseek R1:
KMP算法中的next数组是一个核心组件,用于记录模式字符串的前缀和后缀的最长公共元素长度,以便在主字符串中进行高效的模式匹配。
next数组的定义和作用
next数组记录了模式字符串的前缀和后缀的最长公共元素长度。在模式匹配过程中,当发生不匹配时,next数组可以帮助确定模式字符串应该滑动多远,以跳过已经匹配过的部分,从而减少不必要的匹配尝试,提高匹配效率。
next数组的计算方法
计算next数组的过程是一个递推的过程:
初始化:next = -1,表示没有相匹配的前后缀;next1 = 0,因为单个字符没有前缀和后缀。
递推计算:对于每个位置j(j > 1),通过比较模式串的第j个字符和第next[j-1]个字符是否相等来确定next[j]的值。如果相等,则next[j] = next[j-1] + 1;如果不相等,则需要回退到更短的相同前后缀,直到找到匹配的前后缀或回退到-1为止。
next数组在KMP算法中的应用
在KMP算法中,next数组通过记录模式字符串的前缀和后缀的最长公共元素长度,帮助算法在匹配失败时确定模式字符串的滑动距离。
代码
//左程云版,70分
#include "bits/stdc++.h"
using namespace std;
const int N=1e6+5;
string a,b;
int la,lb,n[N];
void nArray(){
int j=0;
for(int i=2;i<=lb;i++){
while(j&&b[i]!=b[j])j=n[j];
if(b[i]==b[j])j++;
n[i]=j;
}
return ;
}
void KMP(){
int j=0;
for(int i=0;i<la;i++){
int x=i;
while(a[x]==b[j])x++,j++;
if(j==lb){
cout<<i+1<<endl;
j=n[j];
}
}
return ;
}
int main(){
cin>>a>>b;
la=a.length(),lb=b.length();
nArray();
KMP();
for(int i=0;i<lb;i++)cout<<n[i]<<" ";
return 0;
}
//@皎月半洒花 的题解,100分
#include<iostream>
#include<cstring>
#define MAXN 1000010
using namespace std;
int kmp[MAXN];
int la,lb,j;
char a[MAXN],b[MAXN];
int main()
{
cin>>a+1;
cin>>b+1;
la=strlen(a+1);
lb=strlen(b+1);
for (int i=2;i<=lb;i++)
{
while(j&&b[i]!=b[j+1])
j=kmp[j];
if(b[j+1]==b[i])j++;
kmp[i]=j;
}
j=0;
for(int i=1;i<=la;i++)
{
while(j>0&&b[j+1]!=a[i])
j=kmp[j];
if (b[j+1]==a[i])
j++;
if (j==lb) {cout<<i-lb+1<<endl;j=kmp[j];}
}
for (int i=1;i<=lb;i++)
cout<<kmp[i]<<" ";
return 0;
}
文献参考:哔站:左程云
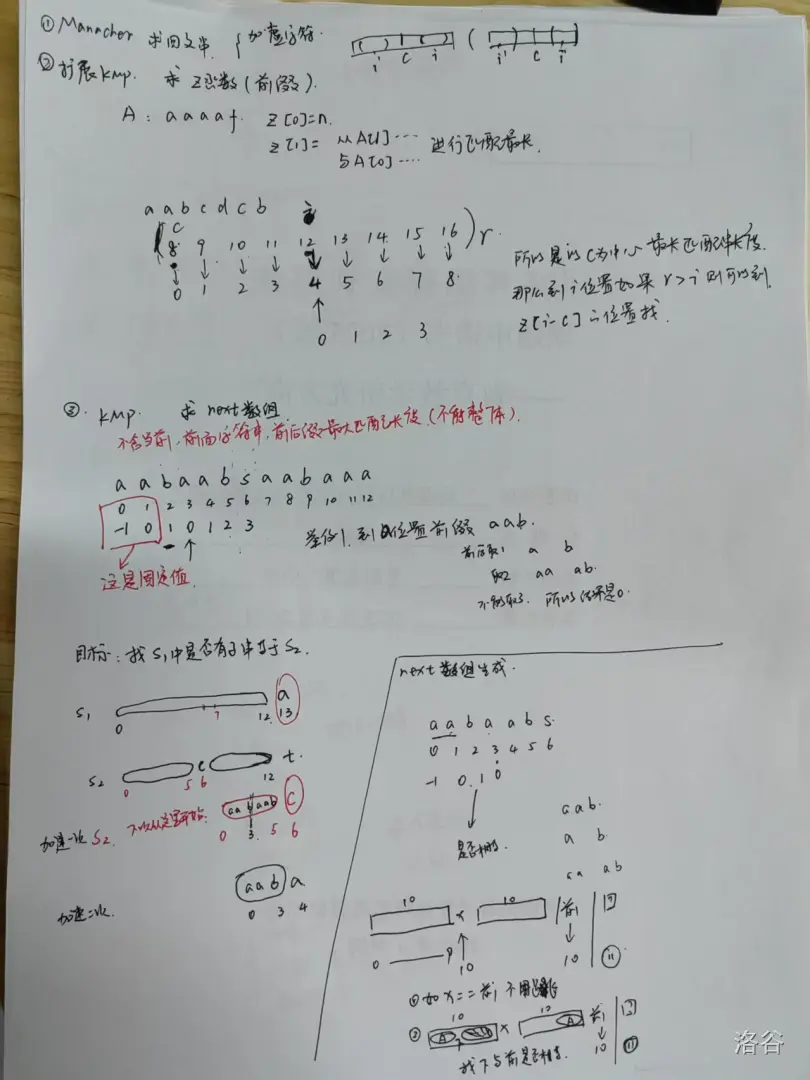
the manuscript of teacher
(老师的手稿)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号