动手学深度学习PyTorch版-task01
task0101.线性回归

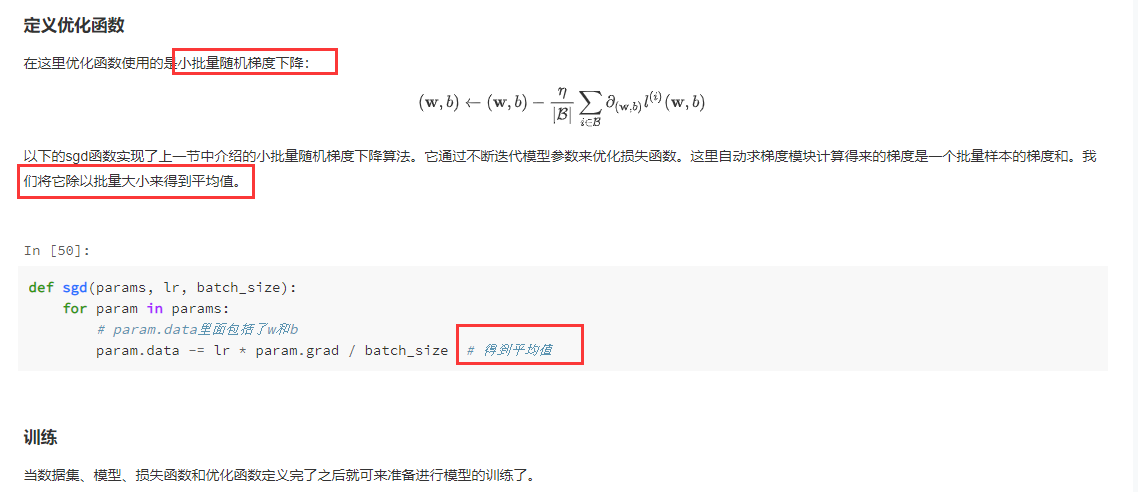
优化函数 - 随机梯度下降
当模型和损失函数形式较为简单时,上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解(analytical solution)。本节使用的线性回归和平方误差刚好属于这个范畴。然而,大多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
在求数值解的优化算法中,小批量随机梯度下降(mini-batch stochastic gradient descent)在深度学习中被广泛使用。它的算法很简单:先选取一组模型参数的初始值,如随机选取;接下来对参数进行多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)β,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。


读取数据时的一段代码理解
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # random read 10 samples
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # the last time may be not enough for a whole batch
yield features.index_select(0, j), labels.index_select(0, j)
测试
In [1]: num_examples = 20
In [2]: indices = list(range(num_examples))
In [3]: indices
Out[3]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
In [4]: random.shuffle(indices)
In [5]: import random
In [6]: random.shuffle(indices)
In [7]: indices
Out[7]: [8, 16, 15, 18, 14, 10, 0, 7, 2, 3, 4, 9, 12, 6, 17, 13, 5, 11, 19, 1]
In [9]: batch_size = 4
In [10]: for i in range(0, num_examples, batch_size):
...: print(i)
...:
0
4
8
12
16
- 问题:随便选了课程代码中的几个小细节,考考大家,有没有人来回答一下~
- torch.mm 和 torch.mul 的区别?
- torch.manual_seed(1)的作用?
- optimizer.zero_grad()的作用?
- 答:
(1)torch.mm是矩阵相乘,torch.mul是按元素相乘
(2)设置随机种子,使实验结果可以复现
(3)使梯度置零,防止不同batch得到的梯度累加
![]()
![]()
课后习题

一个图片解释

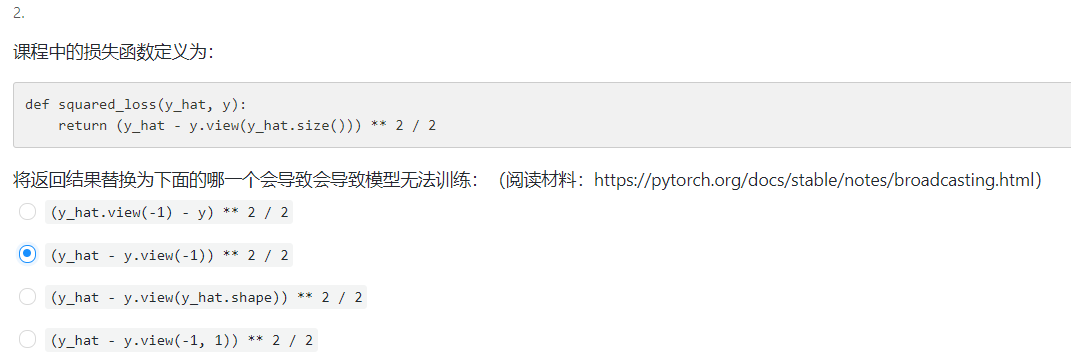
In [12]: import numpy as np
In [13]: y = np.array([1,2,3,4,5,7,8])
In [14]: y.shape
Out[14]: (7,)
In [16]: import torch
In [17]: y = torch.Tensor(y)
In [18]: y.view(-1)
Out[18]: tensor([1., 2., 3., 4., 5., 7., 8.])
In [19]: y.view((-1,1))
Out[19]:
tensor([[1.],
[2.],
[3.],
[4.],
[5.],
[7.],
[8.]])
In [20]: y.view((7,1))
Out[20]:
tensor([[1.],
[2.],
[3.],
[4.],
[5.],
[7.],
[8.]])


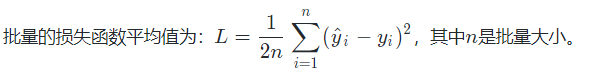
In [22]: 0.5* (1/3)*((2.33-3.14)**2 + (1.07 - 0.98)**2 + (1.23 - 1.32)**2)
Out[22]: 0.11205000000000001
task0102.softmax与分类模型
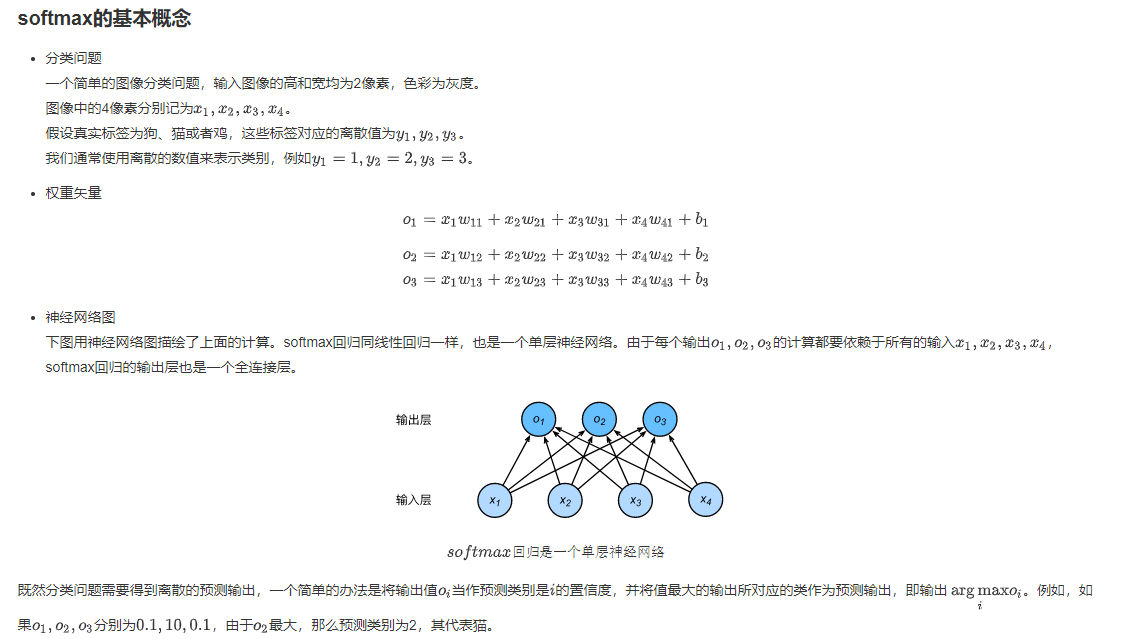


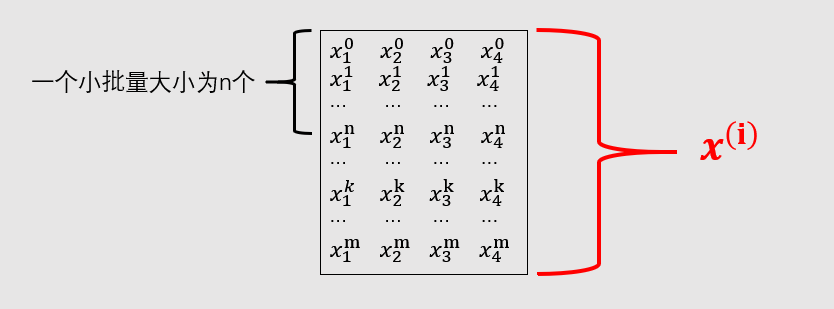
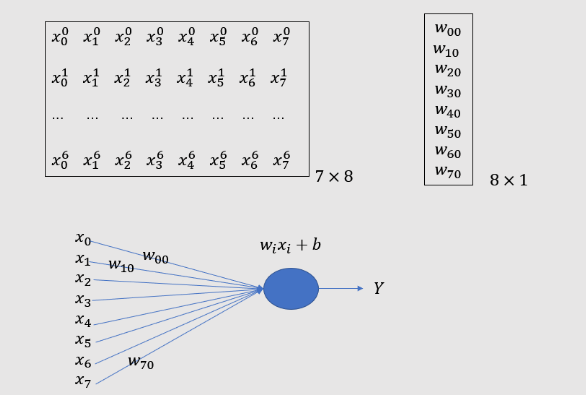
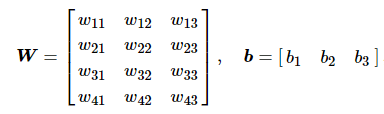
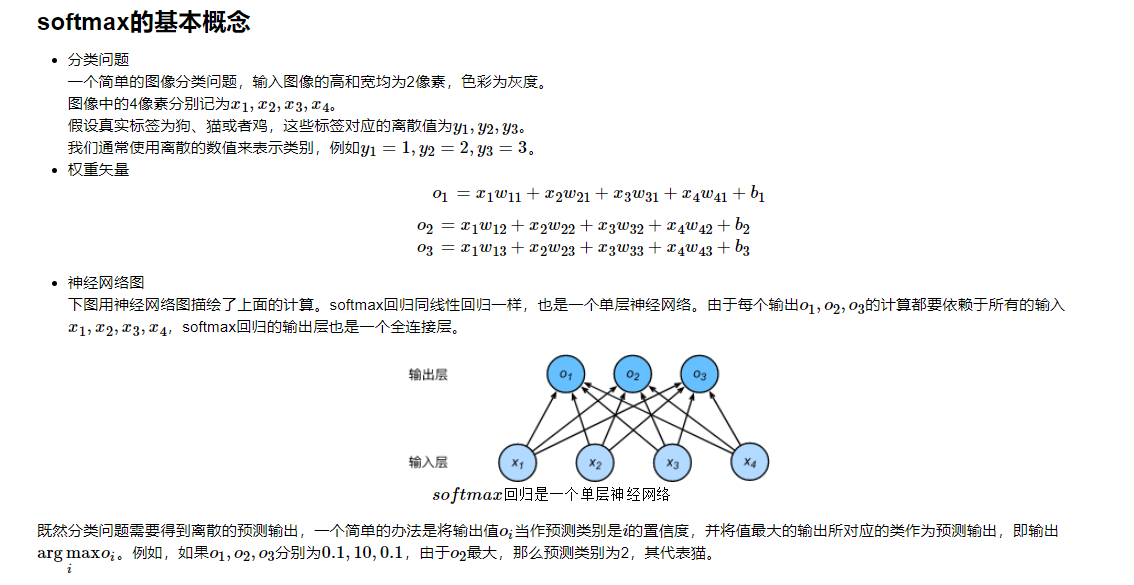
- 这里特征个数d = 4, q = 3(对应输出o(i)的个数或者截距b(i)的个数), W是4×3型,b是1×3型
![]()
![]()


- 交叉熵损失函数原理详解
- 代码片段解读
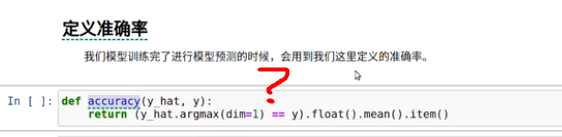
![]()
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) == y).float().mean().item()
- 代码分析
In [23]: y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])^M
...: y = torch.LongTensor([0, 2]) # 真实的标签值
In [24]: y.view(-1, 1)
Out[24]:
tensor([[0],
[2]])
In [25]: y_hat.gather(1, y.view(-1, 1))
Out[25]:
tensor([[0.1000],
[0.5000]])
In [26]: y_hat.argmax(dim=1)
Out[26]: tensor([2, 2])
In [27]: (y_hat.argmax(dim=1) == y)
Out[27]: tensor([0, 1], dtype=torch.uint8) # 第一个预测错误,所以值为0,第二个预测正确,所以值为1
In [28]: (y_hat.argmax(dim=1) == y).float()
Out[28]: tensor([0., 1.])
In [29]: (y_hat.argmax(dim=1) == y).float().mean()
Out[29]: tensor(0.5000)
In [30]: (y_hat.argmax(dim=1) == y).float().mean().item()
Out[30]: 0.5
2个样本里面只对了一个样本(即最后一个),第一个真实值为标签0,但是y_hat将其预测为标签2。
总结
softmax的常数不变性引发的思考:
神经网络中的全部权重同时扩大或减小相同的倍数,softmax分类输出概率不变,交叉熵不变。
因此有必要对神经网络的权重进行正则化,防止权重太大
线性回归:预测连续值,损失函数通常用均方根
SoftMax回归:预测离散值,用于分类,损失函数通常用交叉熵,softMax这一步主要用于归一化,得到概率分布
SoftMax对输出层进行归一化的原因:
1、输出层的输出值的范围不确定,难以直观上判断这些值的意义。
2、由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
交叉熵损失函数 只考虑正确类别的预测概率
课后习题



task0103.多层感知机
-
softmax知识点回顾
![]()
-
多层感知机基本知识
![]()
![]()
![]()
-
关于激活函数的选择
ReLu函数是一个通用的激活函数,目前在大多数情况下使用。但是,ReLU函数只能在隐藏层中使用。
用于分类器时,sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。
在神经网络层数较多的时候,最好使用ReLu函数,ReLu函数比较简单计算量少,而sigmoid和tanh函数计算量大很多。
在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。
课后习题
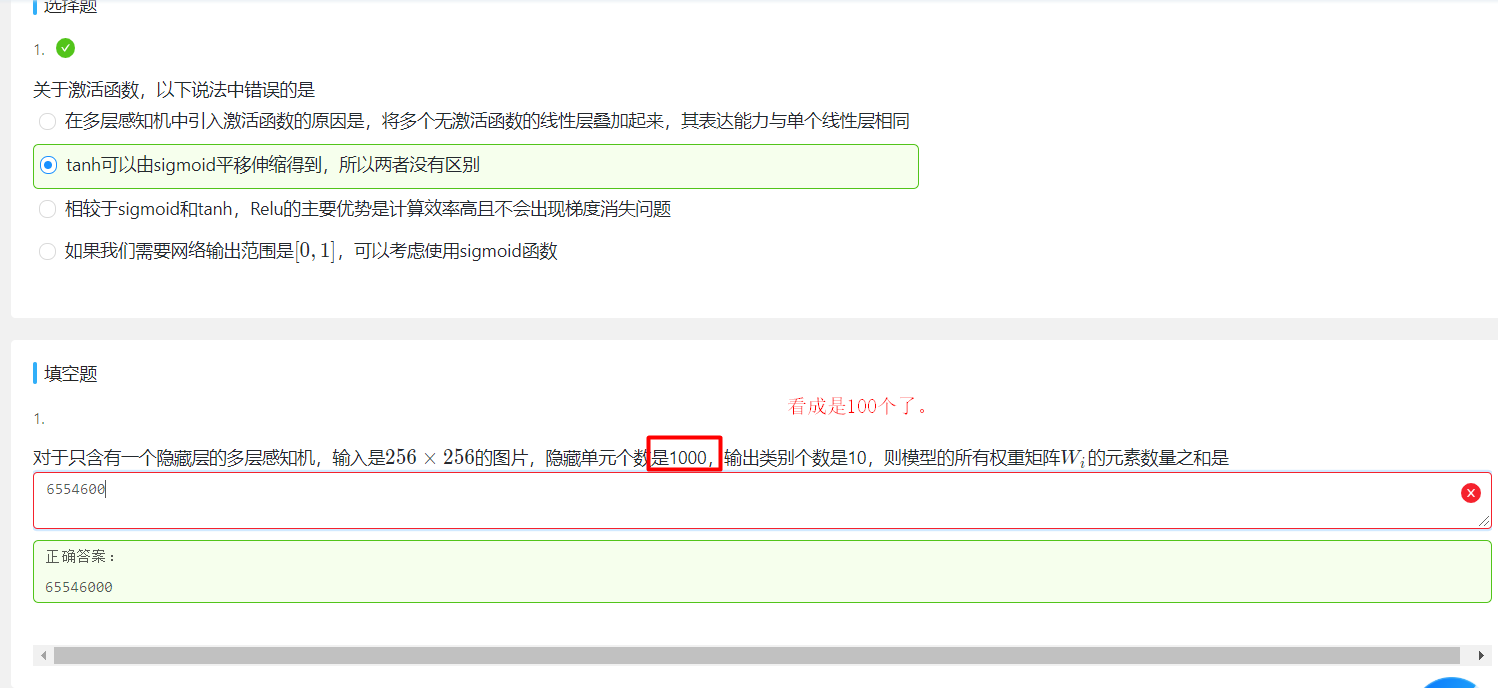

- 知识点补充
(1). PyTorch 的 backward 为什么有一个 grad_variables 参数? - Towser的文章 - 知乎
https://zhuanlan.zhihu.com/p/29923090
假设 x 经过一番计算得到 y,那么 y.backward(w) 求的不是 y 对 x 的导数,而是 l = torch.sum(y*w) 对 x 的导数。w 可以视为 y 的各分量的权重,也可以视为遥远的损失函数 l 对 y 的偏导数。也就是说,不一定需要从计算图最后的节点 y 往前反向传播,从中间某个节点 n 开始传也可以,只要你能把损失函数 l 关于这个节点的导数 dl/dn 记录下来,n.backward(dl/dn) 照样能往前回传,正确地计算出损失函数 l 对于节点 n 之前的节点的导数。特别地,若 y 为标量,w 取默认值 1.0,才是按照我们通常理解的那样,求 y 对 x 的导数。
(2). 详解Pytorch 自动微分里的(vector-Jacobian product) - mathmad的文章 - 知乎 【推荐看看】
https://zhuanlan.zhihu.com/p/65609544







 浙公网安备 33010602011771号
浙公网安备 33010602011771号