机器学习-聚类

前面，提到聚类是无监督学习中应用最广泛的。

聚类

• 定义

   对大量无label的数据集按照样本点之间的内在相似性进行分类，将数据集分为多个类别，使得划分为相同类别的数据的相似度比较大。被划分的每个类称为cluster,

• 距离/相似度计算

欧式距离

   n维空间的任意两点,,之间的距离,由向量性质就是，这本质上是一个2-范式，这里，我们在衡量时用更为广泛的P-范式，至于Pd 取值取决于分类效果。

 余弦相似度

   如果，我们要度量的是文档等字符型的数据之间的距离呢，那么，我们怎么办呢，就不能直接用向量间的距离来度量了，例如，词与词之间的相似性，可以通过某种映射方式，将词映射到向量中，用向量间的夹角来度量，如果夹角大相似性就小，夹角小，相似性就大。

Jaccard 相似度

 

person 相似系数

 相对熵 ：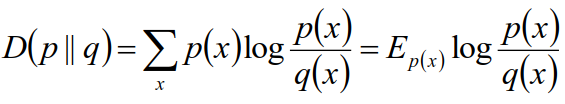 

K-Means 算法

• K-Means 算法过程

顾名思义，k均值，就是分为k类，k-均值算法如下：

• input：数据集，k cluster

1. 从D中随机选择k个样本点作为初始均值向量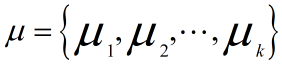作为样本中心
2. 对于D中每个样本点，计算其到中心点的距离，选择最小的一个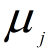作为其中心，并将该样本点的label归为i，用c(i)记录每个样本点所属cluster的index
3. 更新，为中心为上步中中心为的所有样本点的均值，
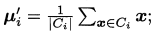
4. 重复上面最后两步，直到的变化小于某个设定的阈值

吴恩达老师的笔记给出的更好，便于实现

 

一点说明：K-Means算法为什么有效是可以证明的，我们假定这每一个cluster的样本都是服从高斯分布的，求得求似然函数，然后求得似然函数的对数，将平方误差作为目标函数，对目标函数求关于的偏导，可以得出，感兴趣的可以手动推一遍

      但是，如果某个cluster中有异常点，就可能导致均值偏离严重，比如，一组很相近的数中有一个数与其他所有数相差很大，这就会造成均值与该cluster中大多数样本点相差很大，这时候，不再取均值作为中心点，而是取中位数

• K-Means 目标优化

先给出吴恩达老师课上给出的目标函数

 聚类方法

层次聚类

自底向上聚类：AGNES算法

每个样本看成一个cluster，计算出两个最近的样本聚合为一个cluster，然后重复前面过程，不断聚合。

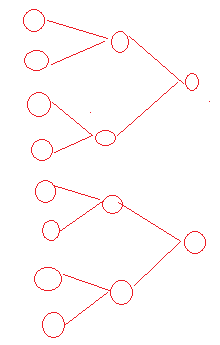
用什么度量cluster之间的距离呢

最小距离：

最大距离：

平均距离：

自自顶向下聚类：DIANA算法

与自底向上过程相反，相对于自底向上，自顶向下不是那么常用

密度聚类方法：DBSCAN算法

根据样本的密度是否与其他样本可连，继而划分为同一个cluster

1.一种基于邻域这一参数来刻画样本的分布的密度（邻域概念可参考高数课本）

我就用周老师书上的图（如下所示）解释一下上面几个概念

不妨设图中的圆域的圆的半径为1，以为例，以为中心的半径小于等于的圆域就是的-邻域，如果MinPts =5,那么就是一个核心对象，在的-邻域内，不在的-邻域内，那么从x1 到x2是直接密度可达的，从x1到x3就不是直接密度可达的，但是从x2到x3是直接米达可达的，那么从x1到x3就是密度相连的，而我们的cluster就是密度相连的点的最大集合

密度聚类会有一个噪声的概念：如果一个样本不在任何cluster中，它就是噪声

简单概括DBSCAN算法的流程就是：

如果一个样本点的-邻域包含至少MinPts个对象，则创建一个作为核心对象的新cluster

寻找并合并核心对象直接密度可达的对象，直到没有可更新的cluster时算法结束