机器学习--支持向量机

• 线性可分SVM

  • hard margin maximization

• 线性SVM

• soft margin maximization
• 非线性SVM
  • kernel function

线性可分SVM

我们先从一个便于理解的二维平面开始，对两类样本进行分类，可以看出至少存在一条线将这两类样本分开，我们要找的模型就是找到这样一条线对数据进行分类，但有时，可能某一个样本，例如，右侧有一个“-”,我们的分割线依然有效，依然是线性可分的。图片来自周志华老师的西瓜书。

 

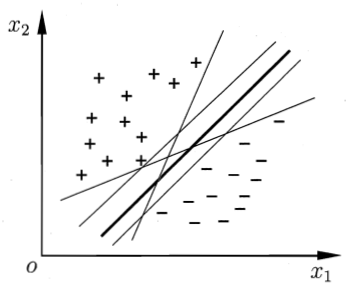
                           图（1） 

为了描述方便，我从其他网站找了如下的图，

 

 

     

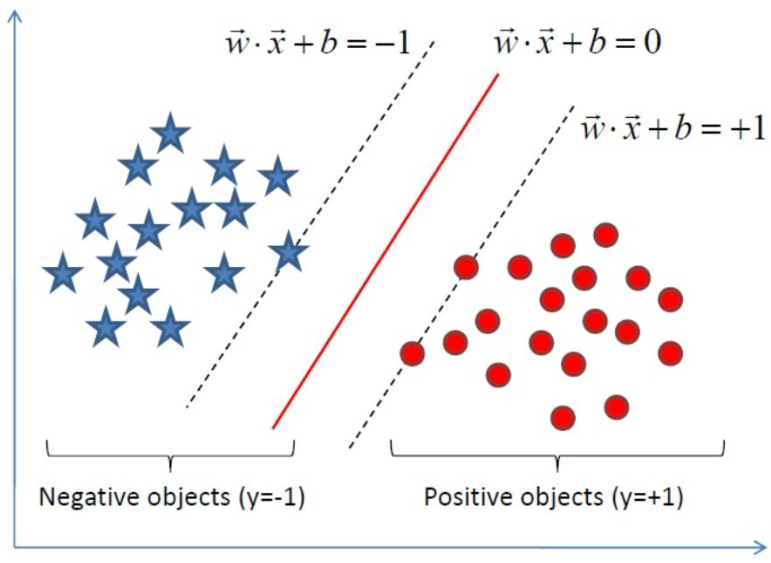
                                        图（2）a                                                                           图（2）b

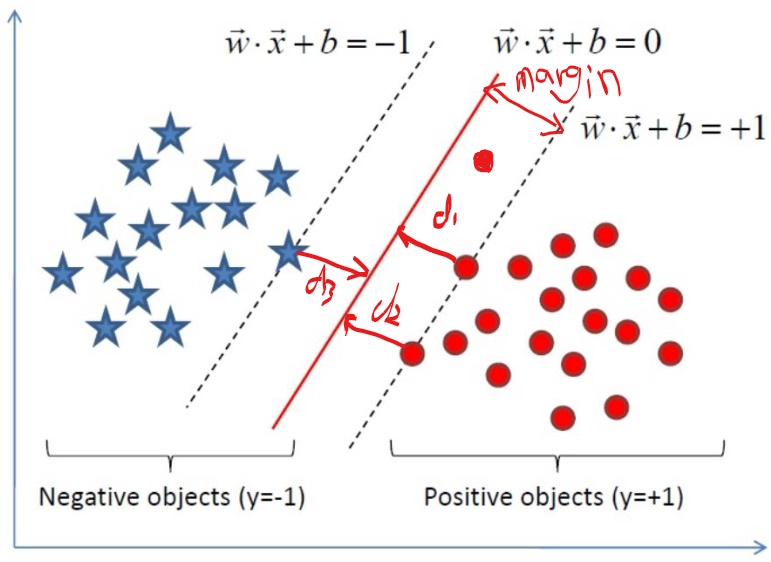
      为什么叫support vector machine,这里先简单一提，后面原理会详细说明，看上图蓝色样本中有一个样本点，红色样本中有两个样本点在虚线上，这三个样本点确定了支撑面，所以这三个样本点就是支撑向量。令这三个点到分割线的距离分别是d1,d2,d3，由数学知识，d1=d2=d3=d,由图可以看出这是距离分割面的最小距离，其他样本点的距离都比这个d大，我们把这个margin称为hard margin，与hard margin相对的就是soft margin ,假如，如图上红色分割线下方有一个我手动画上的一个红色样本点，而我们依然选择这条红色分割线做为我们的分割线，显然，这个样本点距离分割线的距离比刚才的d要小，但我们依然选择刚才的三个样本点作为我们的support vector，现在的margin就是soft margin

 线性可分SVM的原理和目标函数

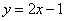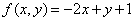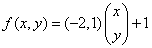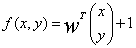首先，看下面的直线,由函数与直线 的关系，该直线的所在函数为，写成向量就是，若将，其中，w就是该直线的法向量，扩展到n维就是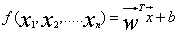，是一个超平面，若是大于零，表明样本点位于方向量方向，小于零就在法向量的负方向。

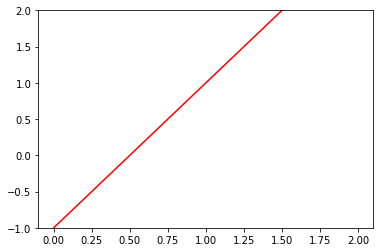
                                          图（3）

直线，由解析几何知识，我们知道点（x0,y0）到直线Ax+By+C=0的距离为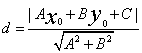，假如现在只考虑正方向，则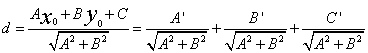，同样，扩展到n维，有一个样本点到分割线的距离就是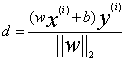，这里w是向量，以下都是这样，不再说明，那么，哪一个是最小的呢。找到最近的样本点，当这个最近的样本点的距离最大时，找到的这条线就是我们要找的分割线，所以对于参数wj,bj，我们要找到这样的wj,bi使得，

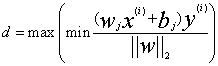下面，我们把数据做一个规定，方便我们推导出目标函数

1.训练集上有n个样本点

2.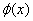表示x的映射后的特征（例如：），那么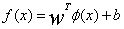，这个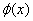我们可以事先选定

那么根据以上设定有：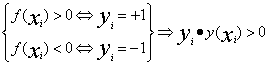

3.我们的目标函数就变成了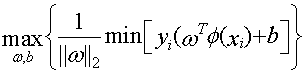，这个式子太过复杂，再看，上面的图（2）b中的超平面，我们总是可以通过放缩使得，分割面的边界线上函数的值为1和-1，因为是放缩，并不会影响最终求得的w,b的值，那么2.中的式子就变成了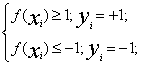，我们的目标函数就简化成了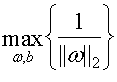，而前面的式子就成了约束条件。

4.我们最终要求的就是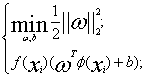，这是一个带约束条件的求最值的问题，由高数知识，可以使用拉格朗日乘子法

最终变成求对偶函数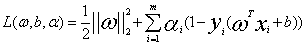，则原问题与对偶问题的关系如下

原问题：

对偶问题：

这里说一下，对于任何一个这样的带约束条件的优化问题，总是可以先写出它的拉格朗日函数，然后去求取关于x的最小值，得到对偶函数，然后，在对偶函数上求关于对偶函数的关于乘子的最大值，只是利用对偶函数，求目标函数，不一定相等

对对偶问题的w,b求偏导有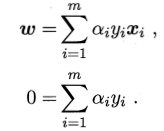，代入到对偶函数中，就是关于的函数了，这样对于那些不等于零的就是support vector，是这些vector确定了分割面，

使用SMO算法求,关于SMO算法，周志华老师的西瓜书写的很详细，先求出，再求出b，然后求出分割超平面w*x+b=0，再求出分类决策函数

 线性SVM

 现实生活中很难确定将数据完全分开的超平面，若样本数据线性不可分，则增加松弛因子，也就就引入上面提到的soft margin，引入一个松弛变量,约束条件变为，目标函数为，则拉格朗日函数为，分别对求偏导有

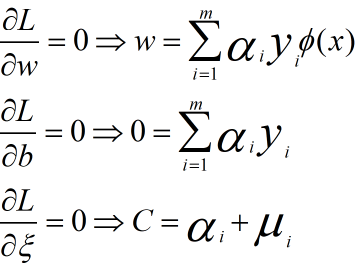，代入到L函数中，得到对偶函数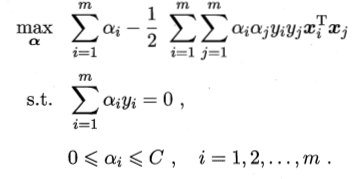，求得最优解，再求出b,然后得到了分割超平面w*x+b=0，最终求的分类决策树。

  损失函数

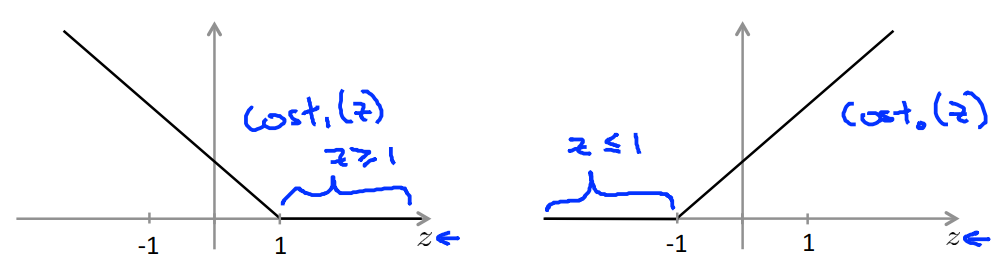
核函数

 并不是所有的样本数据集都是线性可分的，前面就将x映射到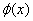，我们也可以使用核函数，将原始输入空间映射到新的特征空间，进而，将原线性不可分的样本映射到核空间

• 线性核 ：
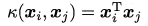
• 多项式核函数：
• 高斯核函数

 

重点说一高斯核在做什么，看一下核函数个表达式，我们可以这样理解，有一个样本点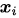，我们假定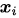是固定的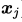，位置不固定，那么就是以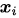为中心做了一个指数衰减，求的是与样本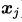的相似度，例如，这两个样本点相等的时候，相似度就是1，如果这两个样本点相距无穷远，相似度就是0，

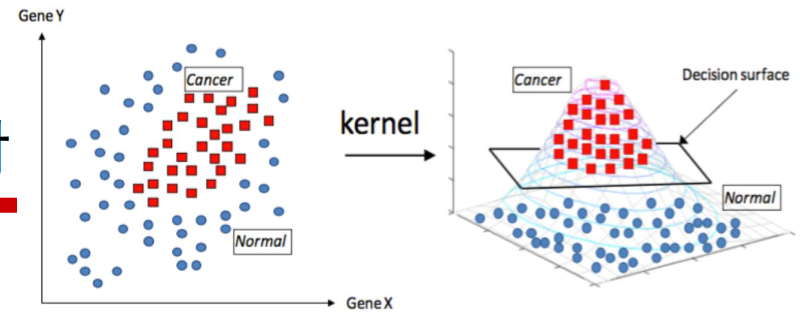
图中，样本点无法做到线性可分，但是，用高斯核函数映射后，对于正例，负例的样本就分开了，分割曲面映射到二维就是分割曲线了，这样，我们就把样本分开了。