【THM】Public Key Cryptography Basics(公钥-密码学基础知识)-学习

本文相关的TryHackMe实验房间链接：https://tryhackme.com/r/room/publickeycrypto

本文相关内容：了解 RSA 等公钥密码的工作原理，并探索它们在 SSH 等应用程序中的作用。

image-20250107223033232

介绍

image-20250105191328292

思考以下日常生活中可能出现的场景。假设你正在与一位业务合作伙伴喝咖啡并讨论一些机密的业务计划，让我们从安全角度来分解一下这样的会议。

  • 你可以看到并听到对方的声音。因此，很容易确定他们的身份。这就是身份验证(authentication)，即你正在确认与你交谈的人的身份。
  • 你还可以确认你所“听到”的内容来自你的业务合作伙伴。你可以分辨出哪些单词和句子来自你的业务伙伴以及哪些单词和句子来自于其他人，这就是真实性(authenticity)，即你可以验证该消息是否真正来自于特定的发件人；而且，你还能够知道他们所说的话已经传到了你的耳朵里，且没有任何机会改变对方的话，这就是完整性(integrity)，即确保数据没有被更改或篡改。
  • 最后，你可以选择远离其他顾客的座位并保持低声，这样只有你的业务伙伴才能听到你的声音，这就是保密性(confidentiality)，即只有授权方才能访问数据。

让我们快速将其与网络领域的通信进行比较。当有人向你发送短信时，你如何确定他们就是他们所声称的人？你如何确定文本在通过各种网络链接进行传输时没有发生任何改变？当你通过在线消息平台与业务合作伙伴进行沟通时，你通常需要注意以下事项：

  • 身份验证(Authentication)：你需要确保与正确的人进行交流，而不是与其他冒充身份的人在进行交流。
  • 真实性(Authenticity)：你可以验证信息是否来自所声明的来源。
  • 完整性(Integrity)：你必须确保没有人更改了你想要交换的数据。
  • 保密性(Confidentiality)：你希望防止未经授权的一方窃听你的对话。

密码学可以提供满足上述这些要求的解决方案。私钥密码学，即对称加密，主要保护的是机密性；然而，公钥密码学，即非对称加密，在身份验证、数据真实性和数据完整性方面发挥着重要作用。本文重点将展示公钥加密方式如何实现安全目标的各种示例。

前置学习基础

与本文相关的TryHackMe实验房间是三个密码学入门实验房间中的第二个。在开始本文的学习之前，请确保你已经完成了下面列表中的第一个实验房间：

学习目标

在本文内容中，我们将介绍各种非对称密码系统以及使用它们的应用程序，例如：

  • RSA
  • Diffie-Hellman(迪菲-赫尔曼)
  • SSH
  • SSL/TLS 证书(Certificates )
  • PGP 和GPG

首先，让我们在与本文相关的TryHackMe实验房间中点击下面的“启动计算机”按钮来启动目标虚拟机。

image-20250109205126500

目标机器将以分屏视图显示。如果目标虚拟机不可见，请尝试使用实验房间页面顶部的蓝色显示拆分视图按钮。

在需要的时候，你可以使用以下凭据(并结合给定的 IP 地址MACHINE_IP)在攻击机上使用SSH来访问刚才部署的目标虚拟机：

  • Username: user
  • Password: Tryhackme123!

非对称加密的常见用途

交换对称加密的密钥是非对称加密技术的广泛用法之一。与对称加密相比，非对称加密的速度相对较慢；因此，我们通常会依靠非对称加密来协商并确定对称加密的密码和密钥。

但问题是，如何在保证不将密钥传输给窥探者查看的情况下 与服务器就密钥方面达成一致？

概念类比

想象一下，你有一个用于通信的密码(Secret Code)以及一些使用该密码的说明。现在的问题是你如何将这些说明发送给你的朋友，而不让其他人去读取它们。答案比看起来更简单；你可以向你的朋友要一把锁(Lock)，只有你的朋友有这把锁的钥匙(Lock’s Key)，我们再假设你有一个可以用这把锁锁上的坚不可摧的盒子。

如果你把说明书放在一个带锁的盒子里寄给你的朋友，那么他们在收到后就能解锁并打开这个盒子来阅读里面的说明书，之后，你和你的朋友之间就可以使用密码来进行通信，而不用担心被人窥探。

在上面这个类比中，密码(Secret Code)代表对称加密密码和密钥(key)，锁(Lock)代表服务器的公钥(public key)，锁的钥匙(Lock’s Key)代表服务器的私钥(private key)。

Analogy 类比 Cryptographic System 密码系统
Secret Code 密码 Symmetric Encryption Cipher and Key 对称加密密码和密钥
Lock 锁 Public Key 公钥
Lock’s Key 锁的钥匙 Private Key 私钥

因此，你只需要使用一次非对称加密，这样对速度不会有太大的影响，然后你就可以继续使用对称加密来进行私密通信。

现实场景

实际上，你需要更强大的加密技术来验证与你正在交谈的人的身份是否。这可以通过数字签名和证书来实现，我们将在稍后的讨论中进行探讨。

答题

在上面提出的类比中，什么真实对象与公钥(public key)的概念类似？

lock

image-20250109205239725

RSA公钥加密算法

RSA是一种公钥加密算法，它可以在不安全的通道(信道)上实现安全的数据传输，而对于不安全的通道(信道)，我们预计攻击者会进行信息窃听。

确保RSA安全的数学原理

RSA算法是基于数学上非常复杂的大数因数分解问题而产生的。两个大素数相乘是一个简单的运算；然而，找到一个大数的因数则需要耗费大量的计算资源。

即使在纸上，计算两个素数相乘的结果也很简单，比如 113 × 127 = 14351 ；对于更大的素数，手工计算仍然是一项可行的工作。请查看以下数字示例：

  • 素数(Prime number)1： 982451653031
  • 素数(Prime number)2： 169743212279
  • 它们相乘的结果： 982451653031 × 169743212279 = 166764499494295486767649

另一方面，确定结果 14351 是由哪两个素数相乘得到的(即找到因数)会变得相当棘手，而找到通过相乘得到 166764499494295486767649 结果的两个素数则更具挑战性。

在现实世界中，实际要处理的素数将比上面示例中的素数要大得多。计算机可以轻松地分解 166764499494295486767649 并得到与之相关的因数；但是，计算机无法对超过 600 位的大素数进行分解。你必须承认——得到两个巨大的素数（每个约 300 位）的乘积要比分解它们的乘积更加容易。

数值示例

让我们重新讨论一下非对称加密中的加密、解密和密钥使用。公钥是所有通信者都知道的，用于加密；私钥会受到保护，用于解密，如下图所示。

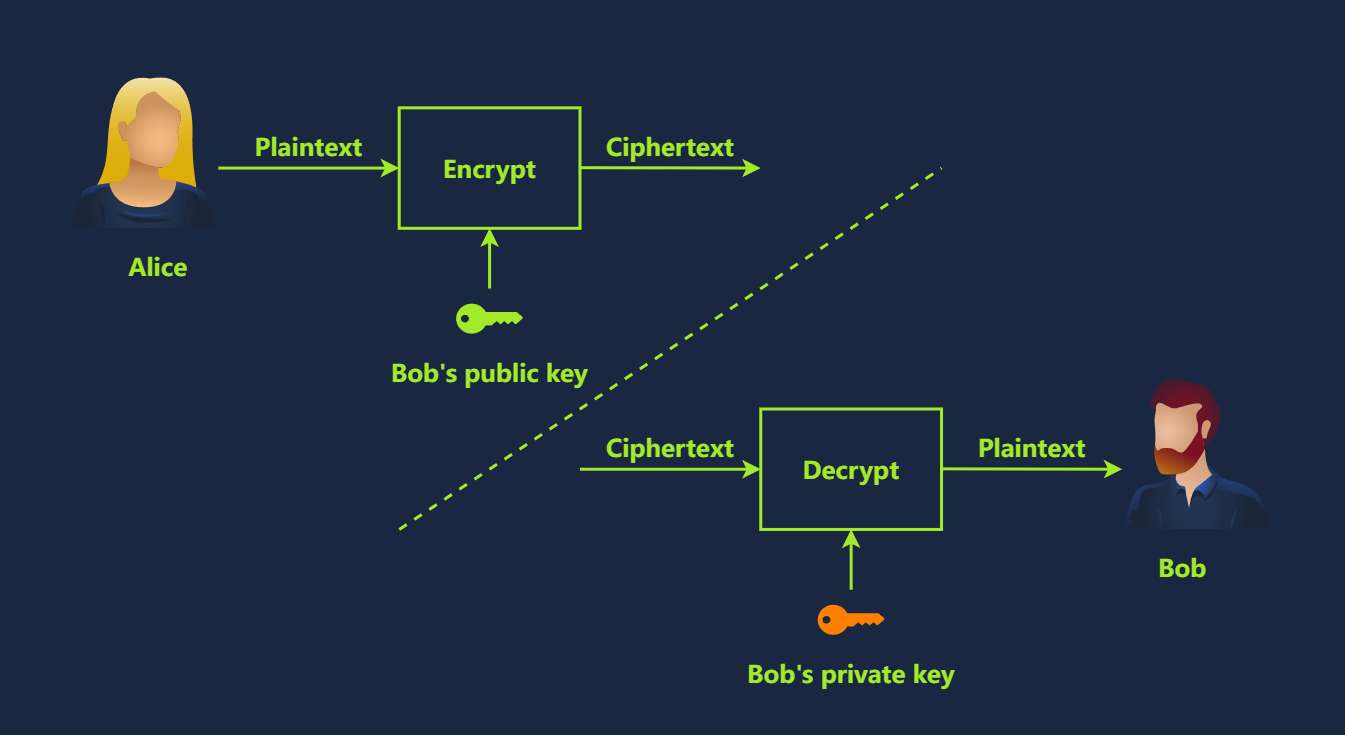
image-20250109205459920

在密码学基础知识实验房间中，我们介绍了模运算，并指出它在密码学中扮演着重要的角色。在下面的简化的数值示例中，我们可以看到RSA算法的具体实现：

  1. Bob选择了两个素数： p = 157 和 q = 199 。他计算 n = p × q = 31243 。

  2. 对于ϕ(n) = n − p − q + 1 = 31243 − 157 − 199 + 1 = 30888 ，Bob选择 e = 163 ，这样的 e 将互质于 ϕ(n) ；此外，他选择 d = 379 ， 而 e × d = 1 mod ϕ(n) ， 即 e × d = 163 × 379 = 61777 以及 61777 mod 30888 = 1 。公钥是 (n,e) ， 即 (31243,163) ；私钥为$(n,d)，即 (31243,379) 。

  3. 假设想要加密的值是 x = 13 ，然后 Alice 将计算并发送 y = x^e mod n = 13^163 mod 31243 = 16341 。

  4. Bob 将通过计算解密收到的值 x = y^d mod n = 16341^379 mod 31243 = 13 ；这样，Bob 就成功将 Alice 所发送的值恢复成明文形式。

    image-20250109205616134

The proof that the above algorithm works can be found in modular arithmetic and is beyond the scope of this module. It is worth repeating that in this example, we picked a three-digit prime number, while in an actual application, p and q would be at least a 300-digit prime number each.

上述算法有效的证明可以在模运算中找到，这超出了本文的讨论范围。值得重申的是，在这个例子中，我们选择了一个三位数的素数，而在实际应用中，p 和q至少会是300位的素数。

CTF中的RSA

RSA 背后的数学原理在 CTF 中出现得比较频繁，通常会要求你计算变量或者破解基于变量的某些加密算法。网络上有很多讲解 RSA 的优秀文章，它们能够为你提供完成与RSA相关的CTF挑战所需的几乎所有信息。 Breaking RSA -破解RSA加密实验房间会是 RSA CTF 挑战的一个很好的例子。

有一些很棒的工具可以帮助你在 CTF 比赛中应对RSA破解挑战。例如RsaCtfTool ，它的使用效果很好，此外rsatool也是一个很好的工具。

你需要了解CTF中与RSA相关的主要变量有：p、q、m、n、e、d 和 c。根据我们的数值示例：

  • p 和 q 是大素数；
  • n 是 p 和 q 的乘积；
  • 公钥是n和e (n,e)；
  • 私钥是n和d (n,d)；
  • m用来表示原始消息，即明文(plaintext)；
  • c表示加密后的文本，即密文(ciphertext)。

Crypto(加密) CTF 挑战通常会向你提供一组相关的变量值，你需要破解加密算法并解密消息以检索最终的flag。

答题

已知p = 4391 和 q = 6659 。那么n 是多少？

n =p × q

29239669

已知p = 4391 和 q = 6659 。那么 ϕ(n) 是多少？

ϕ(n) =n − p − q + 1

29228620

image-20250513005705703

迪菲-赫尔曼(Diffie-Hellman)密钥交换

使用对称加密的挑战之一是密钥共享问题。假设你想要向你的业务合作伙伴发送一份受密码保护的文档，以讨论机密的业务策略。你会如何与他们共享密码？如果有一个安全的通道来发送密码，并且能够确保攻击者无法读取或更改密码，那就最好不过了。

Diffie-Hellman 密钥交换

密钥交换旨在在双方之间建立共享密钥。它是一种允许双方通过不安全的通信通道建立共享密钥的方法，而不需要预先存在的共享密钥，并且观察者也无法获得该密钥。因此，这个共享密钥可以用于后续通信中的对称加密。

假设以下场景：Alice和Bob想要安全地进行通信，他们希望建立一个用于对称加密的共享密钥，但不想使用非对称加密技术来进行密钥交换。这时，Diffie-Hellman 密钥交换就派上用场了。

Alice和Bob各自生成密钥，我们将这些密钥称为 密钥A 和 密钥B，同时他们还有一些公开的共同材料，我们称之为 C。

我们现在需要做出一些假设。首先，每当我们组合密钥时，它们几乎不可能被分离。其次，它们组合的顺序无关紧要。 Alice 和 Bob 会将他们的密钥与公共信息组合，形成 AC 和 BC，然后，他们会将 AC 和 BC 发送给对方，并将接收到的部分与他们的密钥进行组合，从而创建两个相同的密钥，均为 ABC。现在，他们就可以使用这个密钥来进行通信了。

如果你觉得上面的描述太抽象，让我们查看以下步骤来研究一下具体的过程：

  1. Alice 和 Bob 在公共变量上达成一致：一个大素数 p 和一个生成器 g ， 此处 0 < g < p 。这些值将通过通信隧道被公开披露。我们将选择 p = 29 和 g = 3 这样比较小的值来简化计算。
  2. Alice 和 Bob 各自选择一个私有整数，例如，Alice 选择 a = 13 ，Bob 选择 b = 15 。这两个值分别代表一个私钥，且不得泄露。
  3. 现在是 Alice 和 Bob 使用步骤 2 中的私钥与步骤 1 中商定的公共变量来计算各自的公钥的时候了。Alice 计算 A = g^a mod p = 3^13 mod 29 = 19 ，Bob 计算 B = g^b mod p = 3^15 mod 29 = 26 。这些就是公钥。
  4. Alice 和 Bob 互相将密钥发送给对方。Bob 收到 A = g^a mod p = 19 ，即Alice的公钥。Alice收到 B = g^b mod p = 26 ，即 Bob 的公钥。这个步骤被称为密钥交换。
  5. Alice 和 Bob 最终可以使用收到的公钥和他们自己的私钥来计算出共享密钥。Alice计算 B^a mod p = 26^13 mod 29 = 10，Bob计算 A^b mod p = 19^15 mod 29 = 10 。通过计算可以得出相同的结果，即 g^ab mod p = 10 ，这个结果就是最终的共享密钥。

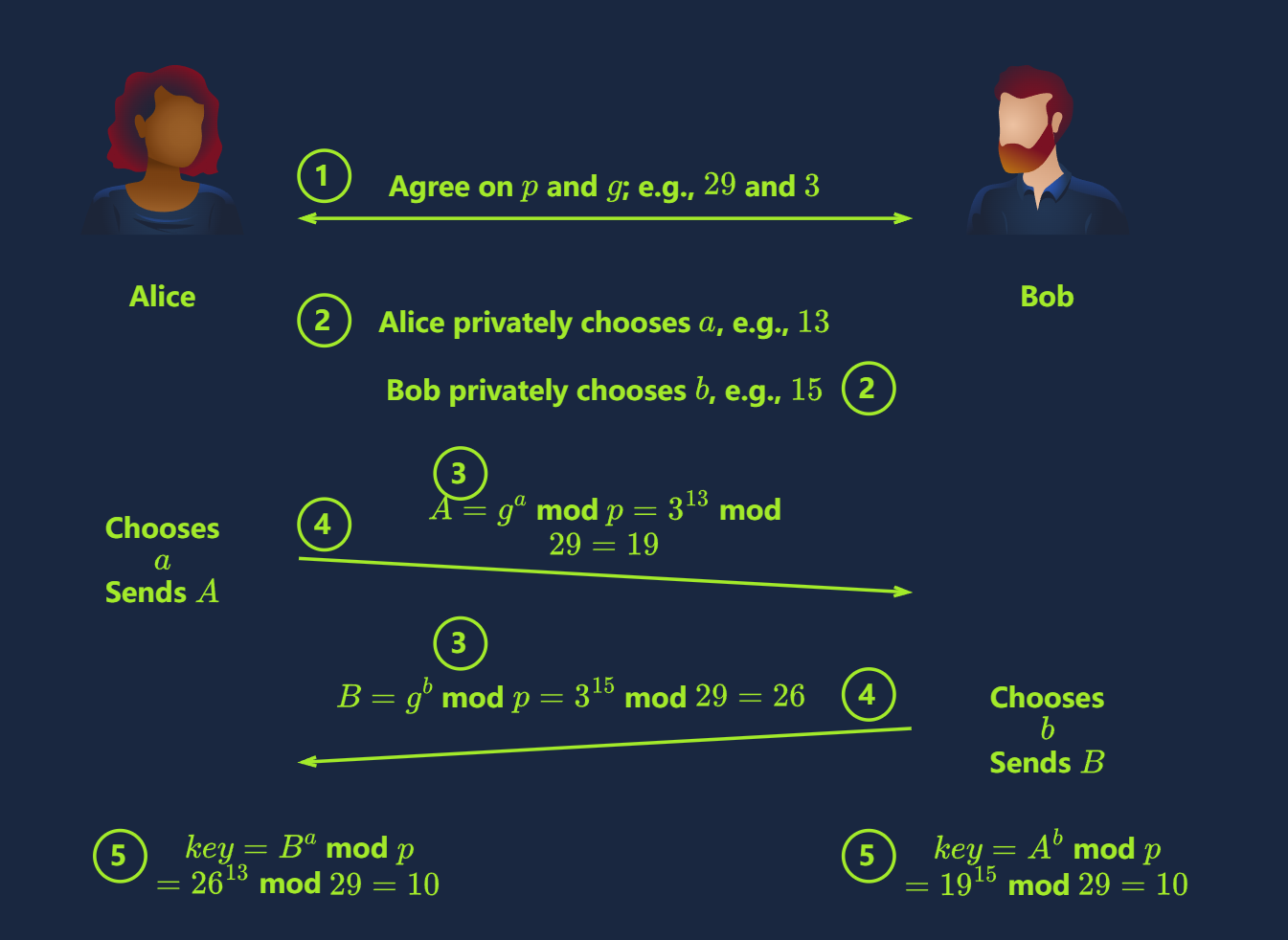
image-20250109210723821

上面示例中所选择的数字其实是比较小的，因此上面的示例将无法确保实际的安全性，而在实际应用中，我们会考虑使用更大的数字。

Diffie-Hellman 密钥交换通常会与RSA公钥加密技术一起使用。 Diffie-Hellman 用于密钥协商，而 RSA 用于数字签名、密钥传输和身份验证等诸多用途。例如， RSA可以通过数字签名来验证与你交谈的人的身份，你可以根据对方的公钥进行确认。这能够防止有人冒充Bob 来对Alice 进行中间人攻击。简而言之，Diffie-Hellman 和 RSA 已经被纳入到了很多安全协议和标准中，以提供全面的安全解决方案。

答题

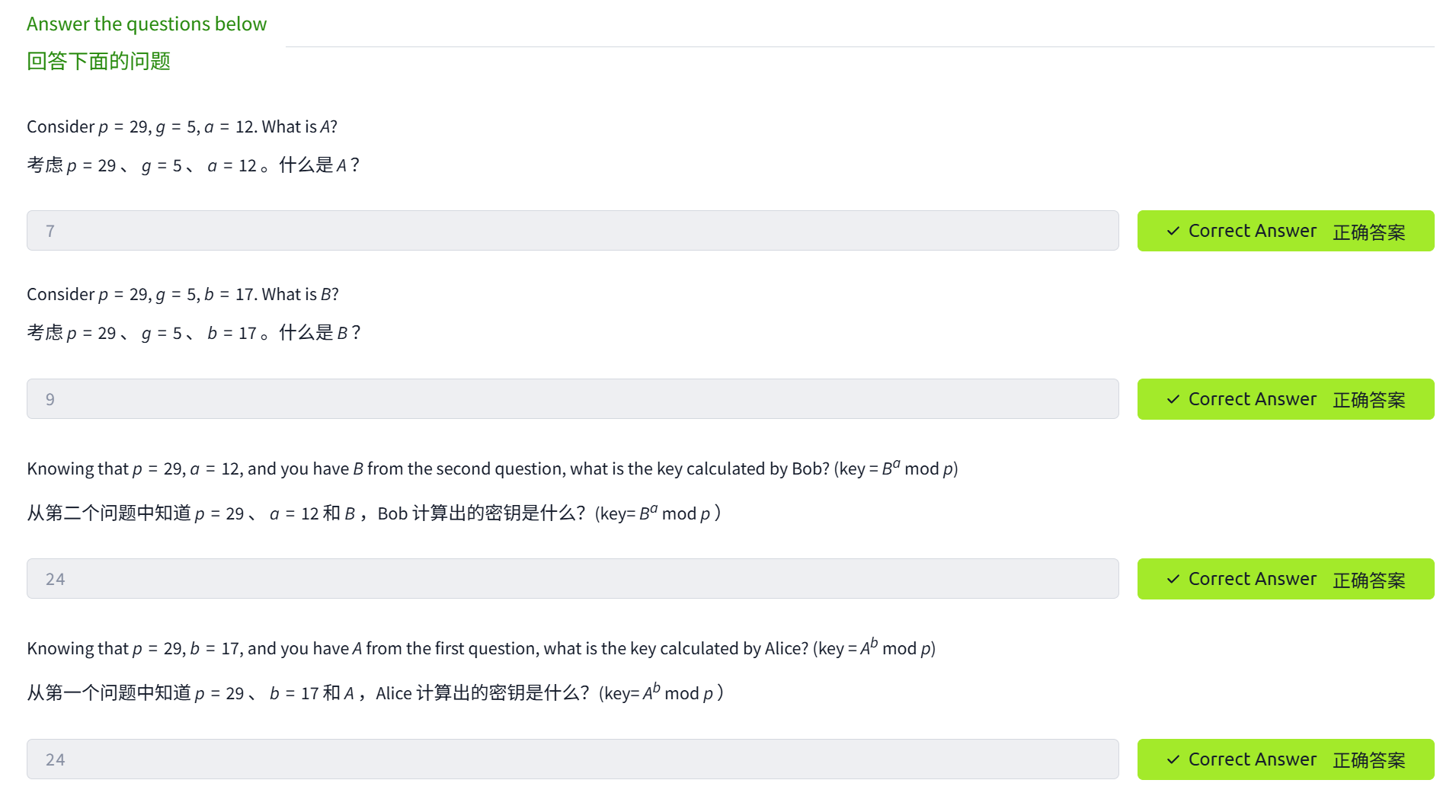
已知 p = 29 , g = 5 , a = 12 ；什么是 A ？

A = g^a mod p

7

已知 p = 29 , g = 5 , b = 17 ；什么是 B ？

B = g^b mod p

9

从第二个问题中知道 p = 29 , a = 12 ，并且你现在已经得到了 B ，那么Bob计算出的密钥是多少？ （key = B^a mod p ）

24

从第一个问题中知道 p = 29 , b = 17 ，并且你现在已经得到了 A ，那么Alice计算出的密钥是多少？ （key = A^b mod p ）

24

image-20250513010644272

SSH身份验证密钥

验证服务器身份

如果你以前使用过SSH客户端，你就会知道下面的终端输出示例中的确认提示。

root@TryHackMe# ssh 10.10.244.173
The authenticity of host '10.10.244.173 (10.10.244.173)' can't be established.
ED25519 key fingerprint is SHA256:lLzhZc7YzRBDchm02qTX0qsLqeeiTCJg5ipOT0E/YM8.
This key is not known by any other name.
Are you sure you want to continue connecting (yes/no/[fingerprint])? yes
Warning: Permanently added '10.10.244.173' (ED25519) to the list of known hosts.

在上面的Shell交互过程中， SSH客户端将确认我们是否识别服务器的公钥指纹。 ED25519 是示例中用于生成和验证数字签名的公钥算法。我们的SSH客户端无法识别此密钥，并要求我们确认是否要继续连接。出现此警告是因为可能存在中间人攻击；恶意服务器可能会拦截连接并回复，以伪装成目标服务器。

在这种情况下，用户必须对服务器进行身份验证，即通过检查公钥签名来确认服务器的身份。一旦你回答“yes”， SSH客户端就会记录此主机的公钥签名。将来，除非该主机选择使用不同的公钥回复，否则将会以静默方式连接到你的SSH客户端所在的机器。

验证客户端身份

现在我们已经确认我们正在与正确的服务器通信，接下来我们还需要识别自己的身份并进行身份验证。很多情况下， SSH用户会使用用户名和密码进行身份验证，就像登录物理机一样；然而，考虑到密码本身可能存在的问题，这并不符合最佳的安全实践。

在某些时候，人们肯定会遇到配置了密钥身份验证的SSH设备。此身份验证使用公钥和私钥来证明客户端是服务器上的有效且经过授权的用户。默认情况下， SSH服务所使用的密钥会是 RSA 密钥。你可以选择使用哪种算法来生成密钥 并且添加密码来加密SSH密钥。

ssh-keygen是通常用于生成密钥对的程序。它支持多种算法，如下面的手册页所示。

root@TryHackMe# man ssh-keygen
[...]
-t dsa | ecdsa | ecdsa-sk | ed25519 | ed25519-sk | rsa
Specifies the type of key to create. The possible values are “dsa”, “ecdsa”, “ecdsa-sk”, “ed25519”, “ed25519-sk”, or “rsa”.
[...]

以下内容仅供参考。目前，只建议你能够认识它们的名字。

  • DSA(Digital Signature Algorithm-数字签名算法)是一种专门为数字签名设计的公钥密码算法。
  • ECDSA(Elliptic Curve Digital Signature Algorithm-椭圆曲线数字签名算法)是 DSA 的一种变体，它使用椭圆曲线加密技术来提供更小的密钥sizes以实现同等的安全性。
  • ECDSA-SK(ECDSA with Security Key-带安全密钥的ECDSA) 是 ECDSA 的扩展。它集成了基于硬件的安全密钥，以增强私钥保护。
  • Ed25519是一种使用 EdDSA（Edwards曲线数字签名算法）和 Curve25519 的公钥签名系统。
  • Ed25519-SK(Ed25519 with Security Key-带安全密钥的 Ed25519)是 Ed25519 的一种变体。与 ECDSA-SK 类似，它使用基于硬件的安全密钥来增强私钥保护。

让我们使用默认的参数选项来生成一个密钥对：

root@TryHackMe# ssh-keygen -t ed25519
Generating public/private ed25519 key pair.
Enter file in which to save the key (/home/strategos/.ssh/id_ed25519): 
Enter passphrase (empty for no passphrase): 
Enter same passphrase again: 
Your identification has been saved in /home/strategos/.ssh/id_ed25519
Your public key has been saved in /home/strategos/.ssh/id_ed25519.pub
The key fingerprint is:
SHA256:4S4DQvRfp52UuNwg++nTcWlnITEJTbMcCU0N8UYC1do strategos@g5000
The key's random art image is:
+--[ED25519 256]--+
|  .       +XXB.  |
| . .     . oBBo  |
|  . . . = + o=o  |
| .   . * X .o.E  |
|  . . o S +  o . |
|   . . o .. + o  |
|      o +. + o   |
|       +. .      |
|        ..       |
+----[SHA256]-----+

在上面的示例中，我们并没有使用密码短语来保护私钥的内容。让我们看看生成的公钥id_ed25519.pub和生成的私钥id_ed25519 。

strategos@g5000:~/.ssh$ cat id_ed25519.pub 
ssh-ed25519 AAAAC3NzaC1lZDI1NTE5AAAAINqNMqNhpXZGt6T8Q8bOplyTeldfWq3T3RyNJTmTMJq9 strategos@g5000
strategos@g5000:~/.ssh$ cat id_ed25519
-----BEGIN OPENSSH PRIVATE KEY-----
b3BlbnNzaC1rZXktdjEAAAAABG5vbmUAAAAEbm9uZQAAAAAAAAABAAAAMwAAAAtzc2gtZW
QyNTUxOQAAACDajTKjYaV2Rrek/EPGzqZck3pXX1qt090cjSU5kzCavQAAAJA+E+ajPhPm
owAAAAtzc2gtZWQyNTUxOQAAACDajTKjYaV2Rrek/EPGzqZck3pXX1qt090cjSU5kzCavQ
AAAEB981T2ngdoNm8gEzRU35bGHofqRMjfo5egxl0/9fap/NqNMqNhpXZGt6T8Q8bOplyT
eldfWq3T3RyNJTmTMJq9AAAACm9xYWJAZzUwMDABAgM=
-----END OPENSSH PRIVATE KEY-----

请注意，上面共享的私钥仅用于演示目的，随后会被清除。共享私钥将是任何人对其自身安全所能做出的最不安全的行为。此外，如果我们使用-t rsa选项，生成的密钥会更长。

SSH 私钥

正如刚才提到的，你应该像对待密码一样对待你的SSH私钥。在任何情况下都不要分享它们；它们被称为私钥是有原因的。拥有你的私钥的人可以登录到接受它的服务器，即，将其包含在授权密钥中，除非该密钥使用密码加密。

需要特别指出的是，用于解密私钥的密码短语根本无法向服务器表明你的身份；它只会解密SSH私钥。这个密码短语永远不会被传输，也永远不会离开你的系统。

通过使用 John the Ripper 之类的工具，你可以攻击加密的SSH密钥以尝试找到相关的密码短语，这凸显了使用复杂的密码短语以及保持私钥私密性的重要性。

当生成用于登录远程计算机的SSH密钥时，你应该在你的本地计算机上生成密钥，然后再复制公钥到远程计算机中，这里我们可以使用ssh-copy-id命令上传公钥到目标计算机上(目标计算机上永远不会存在对应的私钥)。不过，对于用来访问 CTF 机器而生成的临时密钥来说，这并不重要。

必须正确设置权限才能使用SSH私钥；否则，你的SSH客户端将忽略该文件并发出警告。只有文件所有者才能读取或写入私钥（ 600权限或更严格的权限设置）。命令 ssh -i privateKeyFileName user@host 是为标准Linux OpenSSH 客户端指定密钥的方式。

远程主机所信任的密钥

~/.ssh文件夹是OpenSSH 密钥的默认存储位置。此目录中的authorized_keys（请注意，这是美式英语拼写）文件保存着公钥，如果启用了密钥认证，这些公钥将被允许访问服务器。许多 Linux 发行版默认会启用密钥认证，因为它比使用密码进行身份验证更加安全。如果你想允许 root 用户进行SSH访问，则应该只接受密钥认证(身份验证)。

使用SSH密钥获得“更好的 Shell”

在 CTF、渗透测试和红队演练期间， 假设用户已启用登录，SSH密钥是“升级”反向 shell 的绝佳方式。请注意，www-data 用户通常不允许这样做，但 普通用户 和 root用户可以使用这种方式。将SSH密钥保留在目标机器的 authorized_keys 文件中可以成为一个有用的后门，而且无需处理任何不稳定的反向shell问题，例如 Control-C 或缺少Tab键补全。

答题

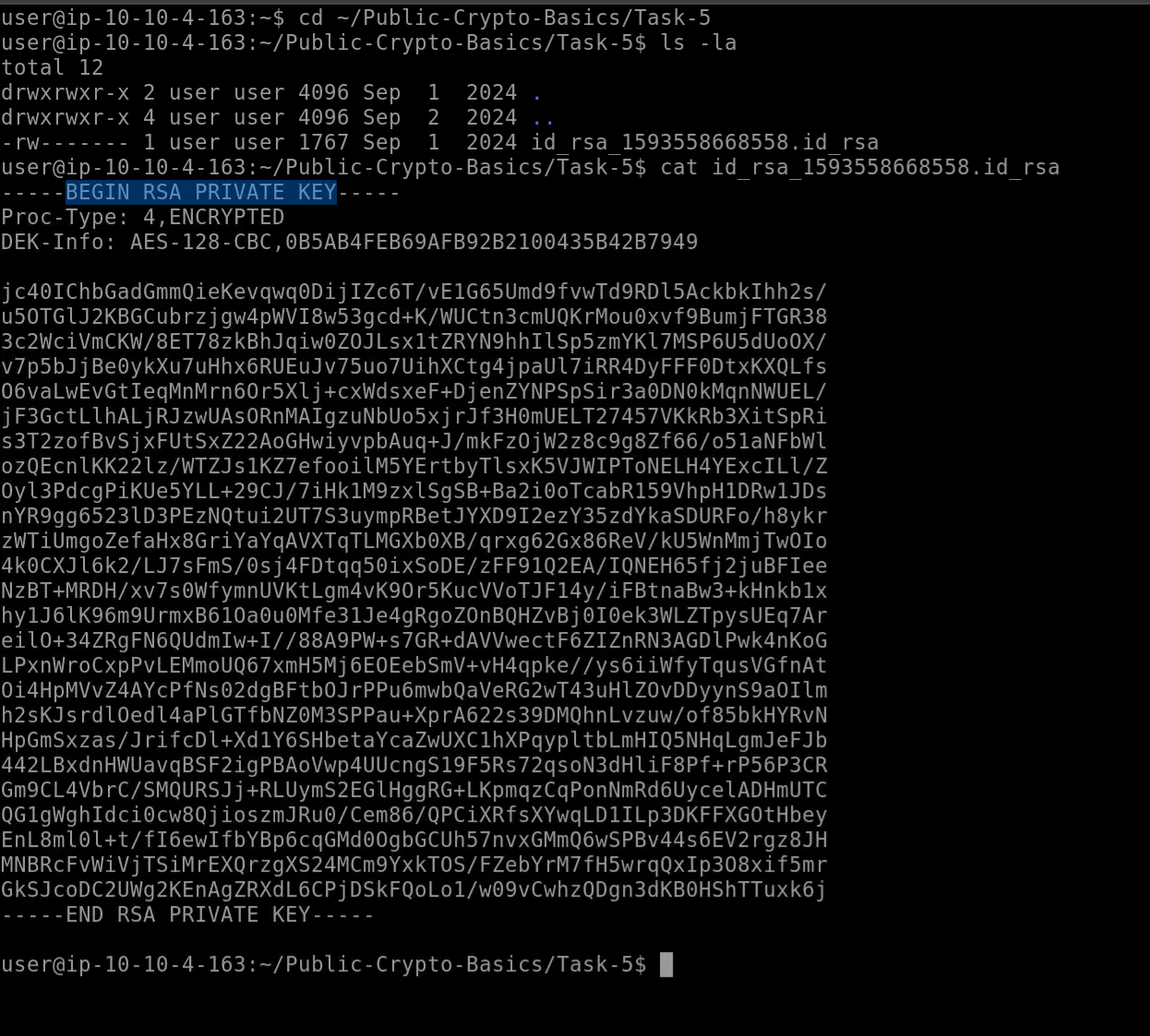
检查~/Public-Crypto-Basics/Task-5中的 SSH 私钥，此密钥是使用什么算法生成的？

tips：部署实验环境，在目标机的终端界面中进行操作。

cd ~/Public-Crypto-Basics/Task-5
ls -la
cat id_rsa_1593558668558.id_rsa #或者使用命令 head -n 3 id_rsa_1593558668558.id_rsa 查看前三行内容
#修改权限：chmod 600 id_rsa_1593558668558.id_rsa
#查看指纹(这条命令会执行失败，因为此命令默认无法直接读取加密的私钥文件)：ssh-keygen -l -f id_rsa_1593558668558.id_rsa
#检查文件类型：file id_rsa_1593558668558.id_rsa
######完整的终端界面操作######
user@ip-10-10-4-163:~$ cd ~/Public-Crypto-Basics/Task-5
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-5$ ls -la
total 12
drwxrwxr-x 2 user user 4096 Sep  1  2024 .
drwxrwxr-x 4 user user 4096 Sep  2  2024 ..
-rw------- 1 user user 1767 Sep  1  2024 id_rsa_1593558668558.id_rsa
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-5$ cat id_rsa_1593558668558.id_rsa
-----BEGIN RSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: AES-128-CBC,0B5AB4FEB69AFB92B2100435B42B7949

jc40IChbGadGmmQieKevqwq0DijIZc6T/vE1G65Umd9fvwTd9RDl5AckbkIhh2s/
u5OTGlJ2KBGCubrzjgw4pWVI8w53gcd+K/WUCtn3cmUQKrMou0xvf9BumjFTGR38
3c2WciVmCKW/8ET78zkBhJqiw0ZOJLsx1tZRYN9hhIlSp5zmYKl7MSP6U5dUoOX/
v7p5bJjBe0ykXu7uHhx6RUEuJv75uo7UihXCtg4jpaUl7iRR4DyFFF0DtxKXQLfs
O6vaLwEvGtIeqMnMrn6Or5Xlj+cxWdsxeF+DjenZYNPSpSir3a0DN0kMqnNWUEL/
jF3GctLlhALjRJzwUAsORnMAIgzuNbUo5xjrJf3H0mUELT27457VKkRb3XitSpRi
s3T2zofBvSjxFUtSxZ22AoGHwiyvpbAuq+J/mkFzOjW2z8c9g8Zf66/o51aNFbWl
ozQEcnlKK22lz/WTZJs1KZ7efooilM5YErtbyTlsxK5VJWIPToNELH4YExcILl/Z
Oyl3PdcgPiKUe5YLL+29CJ/7iHk1M9zxlSgSB+Ba2i0oTcabR159VhpH1DRw1JDs
nYR9gg6523lD3PEzNQtui2UT7S3uympRBetJYXD9I2ezY35zdYkaSDURFo/h8ykr
zWTiUmgoZefaHx8GriYaYqAVXTqTLMGXb0XB/qrxg62Gx86ReV/kU5WnMmjTwOIo
4k0CXJl6k2/LJ7sFmS/0sj4FDtqq50ixSoDE/zFF91Q2EA/IQNEH65fj2juBFIee
NzBT+MRDH/xv7s0WfymnUVKtLgm4vK9Or5KucVVoTJF14y/iFBtnaBw3+kHnkb1x
hy1J6lK96m9UrmxB61Oa0u0Mfe31Je4gRgoZOnBQHZvBj0I0ek3WLZTpysUEq7Ar
eilO+34ZRgFN6QUdmIw+I//88A9PW+s7GR+dAVVwectF6ZIZnRN3AGDlPwk4nKoG
LPxnWroCxpPvLEMmoUQ67xmH5Mj6EOEebSmV+vH4qpke//ys6iiWfyTqusVGfnAt
Oi4HpMVvZ4AYcPfNs02dgBFtbOJrPPu6mwbQaVeRG2wT43uHlZOvDDyynS9aOIlm
h2sKJsrdlOedl4aPlGTfbNZ0M3SPPau+XprA622s39DMQhnLvzuw/of85bkHYRvN
HpGmSxzas/JrifcDl+Xd1Y6SHbetaYcaZwUXC1hXPqypltbLmHIQ5NHqLgmJeFJb
442LBxdnHWUavqBSF2igPBAoVwp4UUcngS19F5Rs72qsoN3dHliF8Pf+rP56P3CR
Gm9CL4VbrC/SMQURSJj+RLUymS2EGlHggRG+LKpmqzCqPonNmRd6UycelADHmUTC
QG1gWghIdci0cw8QjioszmJRu0/Cem86/QPCiXRfsXYwqLD1ILp3DKFFXGOtHbey
EnL8ml0l+t/fI6ewIfbYBp6cqGMd0OgbGCUh57nvxGMmQ6wSPBv44s6EV2rgz8JH
MNBRcFvWiVjTSiMrEXQrzgXS24MCm9YxkTOS/FZebYrM7fH5wrqQxIp3O8xif5mr
GkSJcoDC2UWg2KEnAgZRXdL6CPjDSkFQoLo1/w09vCwhzQDgn3dKB0HShTTuxk6j
-----END RSA PRIVATE KEY-----

user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-5$

image-20250515085718375

RSA

image-20250515090516792

数字签名和证书

在“模拟”世界中，你时不时会被要求签署一些文件。当你前往银行开设储蓄账户时，你很可能会被要求签署几份文件；当你想在当地图书馆创建帐户时，系统会要求你填写并签署申请表。申请表的用途可能因情况而异，例如，它可以确认你同意条款和条件、授权交易或确认收到物品。在“数字”世界中，你无法使用你的物理签名、印章或指纹；你需要的是一个数字签名。

什么是数字签名？

数字签名提供了一种验证数字消息或文档的真实性和完整性的方法。证明文件的真实性意味着我们知道谁创建了或修改了它们。使用非对称加密技术，你可以使用你的私钥来生成一个签名，该签名可以使用你的公钥进行验证。只有你有权访问你的私钥，该私钥可以证明你签署了文件。在许多现代国家/地区，数字签名和物理签名具有同等的法律效力。

最简单的数字签名形式是使用你的私钥来对文档进行加密。如果有人想验证此签名，他们会使用你的公钥来进行解密，并检查文件是否匹配。此过程如下图所示。

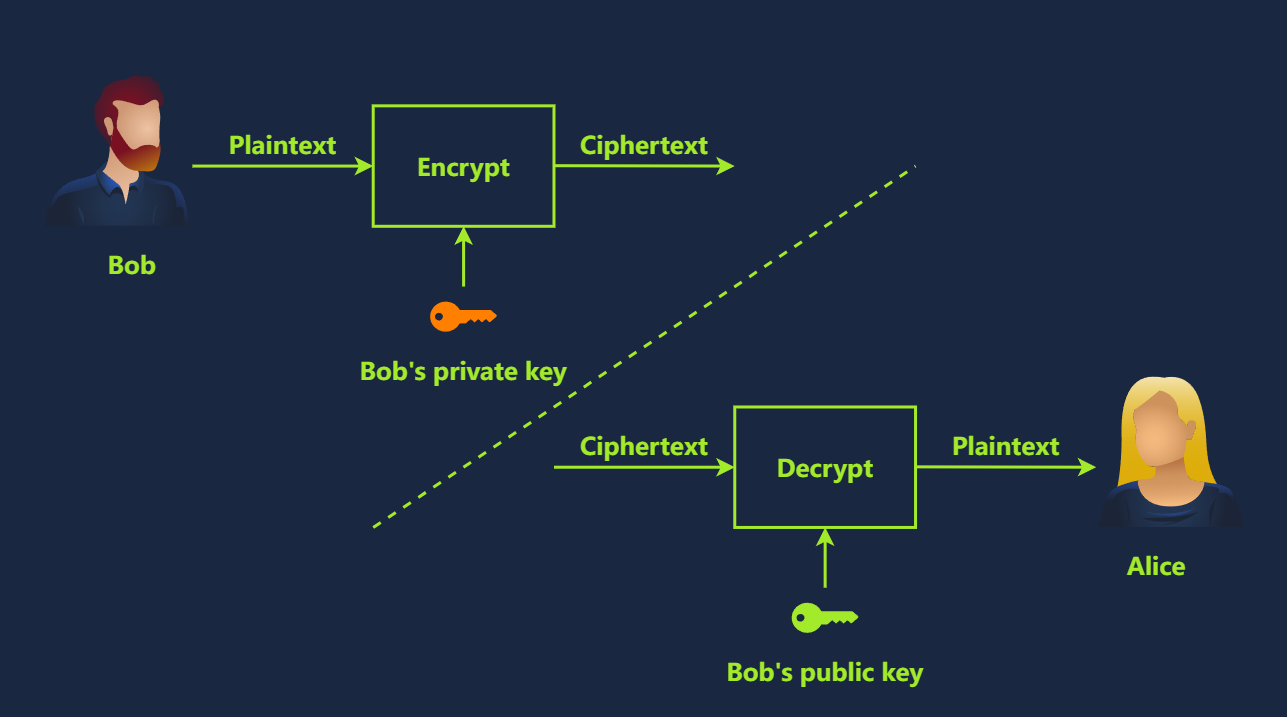
image-20250109211212075

有些文章会交替使用电子签名和数字签名等术语，它们指的是将签名image粘贴到文档顶部，但是这种方法实际上并不能证明文档的完整性，因为任何人都可以复制并粘贴image。

在本小节中，我们会使用术语“数字签名-digital signature”一词来指使用私钥或证书对文档进行签名。此过程与上图所示的情况类似，其中Bob会加密其文档的哈希值，并将其与原始文档一起分享给 Alice ，Alice 可以解密被加密的哈希值并将其与她收到的文件的哈希值进行比较。与粘贴一张精美的签名图片不同，这种方法可以证明文档的完整性。

证书：证明你是谁

证书是公钥加密技术的一个重要应用，它们还与数字签名相关联。证书的常见用途是在HTTPS协议通信中。你的Web浏览器如何知道你正在访问的服务器确实是真正的tryhackme.com？

答案就在于证书。Web服务器拥有一份证书，表明它是真正的tryhackme.com。证书具有一条从 根 CA（证书颁发机构）开始的信任链。从安装时起，你的设备、操作系统和 Web 浏览器就会自动信任各个根 CA。只有当根 CA 表示信任签发证书的机构时，证书才会被信任。从某种程度上来说，它是一个链条；例如，证书由某个机构签署，该机构受到 CA 的信任，而你的浏览器又信任该 CA 。因此，你的浏览器信任该证书。通常，这种信任链会很长。你可以在此处查看 Mozilla Firefox 所信任的证书颁发机构(CA-Certificate Authority)，或者在此处查看 Google Chrome 所信任的证书颁发机构。

假设你有一个网站，并且想要使用 HTTPS ，那么这一步就需要拥有 TLS 证书。你可以从各个证书颁发机构获取证书，并支付年费。此外，你还可以使用Let's Encrypt来免费为你所拥有的域名获取 TLS 证书。如果你在运营一个网站，那么设置并切换到 HTTPS 是值得的，就像任何现代网站都会做的那样。

答题

远程 Web 服务器使用什么来向客户端证明自己的身份？

certificate-证书

你将使用什么来为你的网站获取免费的 TLS 证书？

Let's Encrypt：https://letsencrypt.org/

image-20250513010946388

PGP 和 GPG

PGP代表“良好隐私保护-Pretty Good Privacy”。它是一款用于加密文件、执行数字签名等操作的软件。 GnuPG 或GPG是 OpenPGP 标准的开源实现。

GPG通常在电子邮件中使用，以保护电子邮件信息的机密性；此外，它还可以用于对电子邮件进行签名并确认其完整性。

下面是生成GPG的示例。系统会询问你使用gpg的目的：是仅签名还是签名并加密。除了选择加密算法之外，我们还需要为生成的密钥设置一个到期日期。最后，我们还需要提供一些个人信息：姓名、电子邮件地址以及一些通常与此密钥用途相关的注释。

gpg --full-gen-key
gpg (GnuPG) 2.4.4; Copyright (C) 2024 g10 Code GmbH
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.

Please select what kind of key you want:
   (1) RSA and RSA
   (2) DSA and Elgamal
   (3) DSA (sign only)
   (4) RSA (sign only)
   (9) ECC (sign and encrypt) *default*
  (10) ECC (sign only)
  (14) Existing key from card
Your selection? 9
Please select which elliptic curve you want:
   (1) Curve 25519 *default*
   (4) NIST P-384
   (6) Brainpool P-256
Your selection? 1
Please specify how long the key should be valid.
         0 = key does not expire
      <n>  = key expires in n days
      <n>w = key expires in n weeks
      <n>m = key expires in n months
      <n>y = key expires in n years
Key is valid for? (0) 
Key does not expire at all
Is this correct? (y/N) y

GnuPG needs to construct a user ID to identify your key.

Real name: strategos
Email address: strategos@tryhackme.thm
[...]
pub   ed25519 2024-08-29 [SC]
      AB7E6AA87B6A8E0D159CA7FFE5E63DBD5F83D5ED
uid                      Strategos <strategos@tryhackme.thm>
sub   cv25519 2024-08-29 [E]

你可能需要使用 GPG 来解密 CTF 中的文件。在使用 PGP/GPG时，可以使用密码短语保护私钥，就像我们保护SSH私钥一样。如果密钥受密码短语保护，你可以尝试使用John the Ripper和gpg2john来进行破解。此小节中所提供的密钥不受密码短语的保护。 关于GPG的在线手册页可以在此处找到。

实例

现在你已经有了GPG密钥对，你可以将公钥分享给你的联系人了。每当你的联系人想要安全地进行通信时，他们都会使用你的公钥来加密发送给你的消息。如果想解密消息，你必须使用你的私钥来完成。由于GPG密钥的重要性，请务必将备份副本保存在计算机中安全的位置。

假设你现在买了一台新电脑，你只需要基于备份副本导入密钥，然后你就可以重新解密收到的消息了：

  • 你可以使用gpg --import backup.key从 backup.key 导入你的密钥；
  • 要解密你的消息，你需要发出 gpg --decrypt confidential_message.gpg。

答题

使用 GPG 解密~/Public-Crypto-Basics/Task-7中的消息，该消息包含了什么秘密单词？

cd ~/Public-Crypto-Basics/Task-7
ls -la
gpg --import tryhackme.key
gpg --decrypt message.gpg
######完整的终端界面操作######
user@ip-10-10-4-163:~$ cd ~/Public-Crypto-Basics/Task-7
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-7$ ls -la
total 16
drwxrwxr-x 2 user user 4096 Sep  1  2024 .
drwxrwxr-x 4 user user 4096 Sep  2  2024 ..
-rw-r--r-- 1 user user  263 Sep  1  2024 message.gpg
-rw-r--r-- 1 user user 1367 Sep  1  2024 tryhackme.key
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-7$ gpg --import tryhackme.key
gpg: /home/user/.gnupg/trustdb.gpg: trustdb created
gpg: key FFA4B5252BAEB2E6: public key "TryHackMe (Example Key)" imported
gpg: key FFA4B5252BAEB2E6: secret key imported
gpg: Total number processed: 1
gpg:               imported: 1
gpg:       secret keys read: 1
gpg:   secret keys imported: 1
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-7$ gpg --decrypt message.gpg
gpg: encrypted with rsa1024 key, ID 2A0A5FDC5081B1C5, created 2020-06-30
      "TryHackMe (Example Key)"
You decrypted the file!
The secret word is Pineapple.
user@ip-10-10-4-163:~/Public-Crypto-Basics/Task-7$

image-20250515090946490

Pineapple

image-20250515091327377

本文小结

我们将密码学定义为一门如何在攻击者面前确保通信安全的科学。另外一门研究如何破解或绕过密码系统的重要科学是密码分析学。

尝试每种可能的密码组合来进行攻击的方式，我们称之为暴力猜解攻击；然而，当我们知道密码很可能是某个字典中的单词时，尝试字典中的单词而不是尝试所有可能的密码组合会更加有意义，这种方式被称为字典攻击。

  • 密码学是使用代码和密码保护通信和数据安全的科学。
  • 密码分析学是研究在不知道密钥的情况下 如何破解或绕过密码安全系统的方法 的一门科学。
  • 暴力猜解攻击(Brute-Force Attack)是一种攻击方法，它将尝试所有可能的密钥或密码来解密消息。
  • 字典攻击(Dictionary Attack)是一种攻击方法，攻击者将尝试使用字典中的单词或单词组合来进行攻击。

本文的重点是公钥密码使用方式、非对称密码使用方式和密钥交换，通过学习相关内容能够让你对RSA、Diffie-Hellman、 SSH密钥对、数字签名和证书以及 OpenPGP有一个基本的了解。

posted @ 2025-05-15 09:17  Hekeatsll  阅读(313)  评论(0)    收藏  举报