【力扣】组合总和

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combination-sum

给定一个无重复元素的数组 $candidates$ 和一个目标数 $target$ ，找出 $candidates$ 中所有可以使数字和为 $target$ 的组合。

$candidates$ 中的数字可以无限制重复被选取。

说明：

　　所有数字（包括 target）都是正整数。
　　解集不能包含重复的组合。 
示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
　　[7],
　　[2,2,3]
]
示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
 　　[2,2,2,2],
　　 [2,3,3],
 　　[3,5]
]

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/
来源：力扣（LeetCode）

思路分析：根据示例 1：输入: candidates = [2, 3, 6, 7]，target = 7。

候选数组里有 2，如果找到了组合总和为 7 - 2 = 5 的所有组合，再在之前加上 2 ，就是 7 的所有组合；
同理考虑 3，如果找到了组合总和为 7 - 3 = 4 的所有组合，再在之前加上 3 ，就是 7 的所有组合，依次这样找下去。

这一类问题都需要先画出树形图，然后编码实现

编码通过 深度优先遍历 实现，使用一个列表，在 深度优先遍历 变化的过程中，遍历所有可能的列表并判断当前列表是否符合题目的要求，成为「回溯算法」（个人理解，非形式化定义）。

以下给出的是一种树形图的画法。对于组合来说，还可以根据一个数选和不选画树形图，请参考 官方题解 或者 @elegant-pike 的 评论。

以输入：candidates = [2, 3, 6, 7], target = 7 为例：

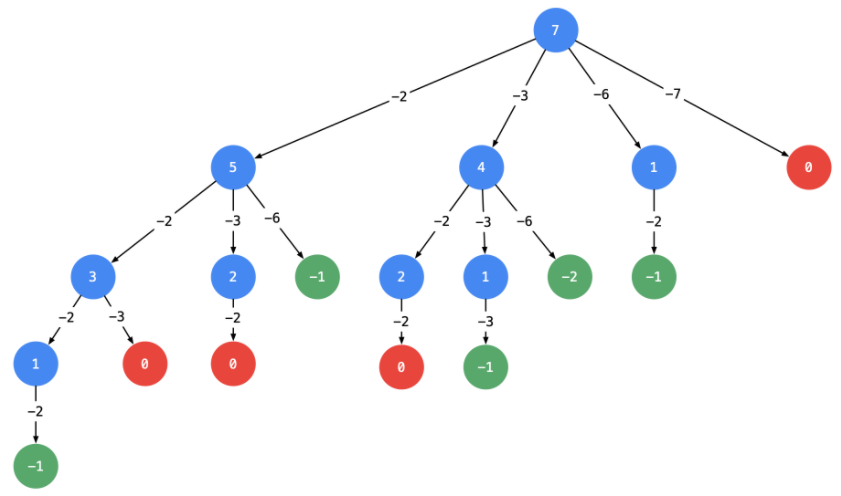
说明：

　　以 target = 7 为 根结点 ，创建一个分支的时 做减法 ；
　　每一个箭头表示：从父亲结点的数值减去边上的数值，得到孩子结点的数值。边的值就是题目中给出的 candidate 数组的每个元素的值；
　　减到 0 或者负数的时候停止，即：结点 0 和负数结点成为叶子结点；
　　所有从根结点到结点 0 的路径（只能从上往下，没有回路）就是题目要找的一个结果。
　　这棵树有 4个叶子结点的值 0，对应的路径列表是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中给出的输出只有 [[7], [2, 2, 3]]。即：题目中要求每一个符合要　　求的解是 不计算顺序 的。下面我们分析为什么会产生重复。

产生重复的原因是：在每一个结点，做减法，展开分支的时候，由于题目中说 每一个元素可以重复使用，我们考虑了 所有的 候选数，因此出现了重复的列表。

一种简单的去重方案是借助哈希表的天然去重的功能，但实际操作一下，就会发现并没有那么容易。

可不可以在搜索的时候就去重呢？答案是可以的。遇到这一类相同元素不计算顺序的问题，我们在搜索的时候就需要 按某种顺序搜索。具体的做法是：每一次搜索的时候设置 下一轮搜索的起点 begin，请看下图。

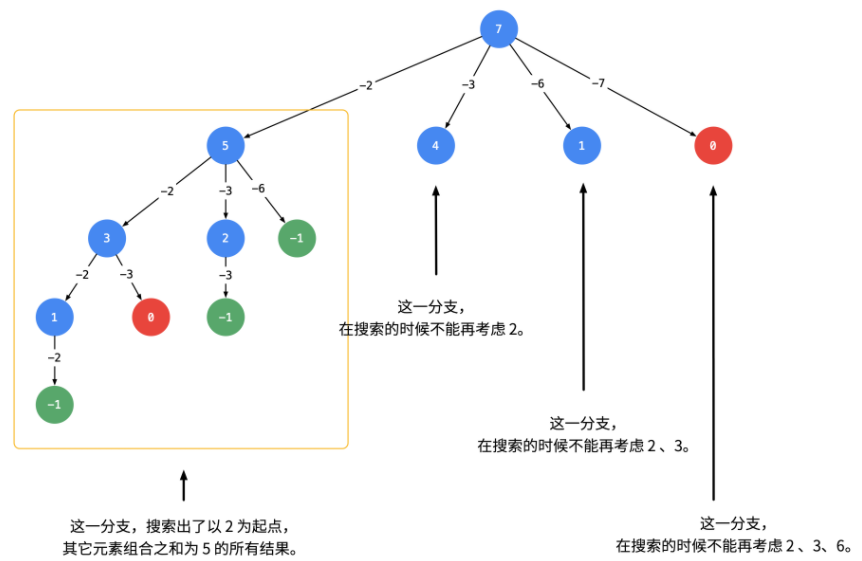
即：从每一层的第 2 个结点开始，都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。

from typing import List


class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:

        def dfs(candidates, begin, size, path, res, target):
            if target < 0:
                return
            if target == 0:
                res.append(path)
                return

            for index in range(begin, size):
                dfs(candidates, index, size, path + [candidates[index]], res, target - candidates[index])

        size = len(candidates)
        if size == 0:
            return []
        path = []
        res = []
        dfs(candidates, 0, size, path, res, target)
        return res

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/
来源：力扣（LeetCode）

剪枝提速
　　根据上面画树形图的经验，如果 target 减去一个数得到负数，那么减去一个更大的树依然是负数，同样搜索不到结果。基于这个想法，我们可以对输入数组进行排序，添加相关逻辑达到进一步剪枝的目的；
　　排序是为了提高搜索速度，对于解决这个问题来说非必要。但是搜索问题一般复杂度较高，能剪枝就尽量剪枝。实际工作中如果遇到两种方案拿捏不准的情况，都试一下。

from typing import List


class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:

        def dfs(candidates, begin, size, path, res, target):
            if target == 0:
                res.append(path)
                return

            for index in range(begin, size):
                residue = target - candidates[index]
                if residue < 0:
                    break

                dfs(candidates, index, size, path + [candidates[index]], res, residue)

        size = len(candidates)
        if size == 0:
            return []
        candidates.sort()
        path = []
        res = []
        dfs(candidates, 0, size, path, res, target)
        return res

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/
来源：力扣（LeetCode）

官方题解

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/combination-sum/solution/zu-he-zong-he-by-leetcode-solution/
来源：力扣（LeetCode）

方法一：搜索回溯
思路与算法

对于这类寻找所有可行解的题，我们都可以尝试用「搜索回溯」的方法来解决。

回到本题，我们定义递归函数 $dfs(target, combine, idx)$ 表示当前在 $candidates$ 数组的第 $idx$ 位，还剩 $target$ 要组合，已经组合的列表为 $combine$。递归的终止条件为 $target <= 0$ 或者 $candidates$ 数组被全部用完。那么在当前的函数中，每次我们可以选择跳过不用第 $idx$ 个数，即执行 $dfs(target, combine, idx + 1)$。也可以选择使用第 $idx$个数，即执行 $dfs(target - candidates[idx], combine, idx)$，注意到每个数字可以被无限制重复选取，因此搜索的下标仍为 $idx$。

更形象化地说，如果我们将整个搜索过程用一个树来表达，即如下图呈现，每次的搜索都会延伸出两个分叉，直到递归的终止条件，这样我们就能不重复且不遗漏地找到所有可行解：

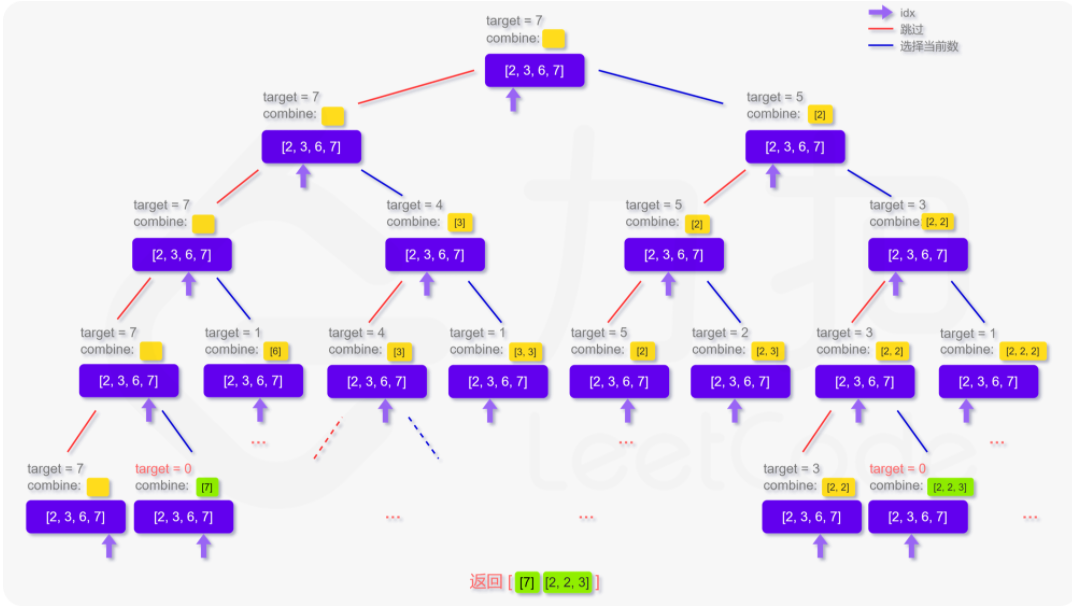
class Solution:
    def combinationSum(self, candidates, target):
        ans = []
        temp = []
        def recursion(idx, res):
            if idx >= len(candidates) or res >= target:
                if res == target:
                    ans.append(temp[:])
                return
            temp.append(candidates[idx])
            recursion(idx, res + candidates[idx]) 
            temp.pop()
            recursion(idx + 1, res)
        recursion(0, 0)
        return ans