BUAA OO Unit1 总结
第一单元的作业是对表达式进行括号展开然后化简,由第一次作业的简单幂函数加括号,到第三次支持求和函数、自定义函数,三角函数与它们之间的嵌套与递归调用,难度逐步增大。在此,我采用的思路都是:
这四步(第二步和第三步应该是同时做的)。因此这几次作业的代码复用率还是挺高的,不至于重构。并且三次作业都由以上思路完成以及拓展导致我在写代码时思路清晰,基本没遇到什么框架上的重大bug
第一次作业
作业思路
架构
第一次作业是关于简单幂函数, 常数并且支持括号(不支持嵌套)的化简,首先我将要存储的结构分为几个部分,如下所示,其中Factor是一个接口,具体逻辑就是:
在了解了存储方法后我采用的方法就是
-
递归下降解析:该部分首先就是先将输入的表达式解析,首先是通过
Lexer类从前往后读取输入的每一个小单元,具体被我分成了:left_bracket、right_bracket(with index)、power、const、plus、minus,然后通过解析类Parser将读到的小单元整合识别并构建相应的存储单元进行数据及其结构的存储 -
展开括号:这应该是最难的一步了,首先放一下框架:
\[Expr.expand \rightarrow Term.expand \rightarrow Expr.mul \rightarrow Term.mul \]-
Expr.expand:就是表达式的展开,其实就是对每一个Term展开,然后对展开完返回的Term进行简单的拆包(即直接提取下文ret的每个Term)后将其加入到res的terms里面,所以该函数调用了Term.expand,最后返回一个叫res的Expr,结构如下:\[(Expr)\ res \rightarrow (many\ Terms)\ Term(const\ |\ const,\ pow) \] -
Term.expand:首先我将Term中不是Expr的因子进行合并,合并结果就是一个只有一个Term的Expr,这个Term中可能是power|const|power and const,然后调用Expr.mul进行Expr的乘法,返回下面示意图中的res。该函数最后返回一个叫ret的Term,返回Term结构如下:\[(Term)\ ret \rightarrow (Expr)\ res \rightarrow (many\ Terms)\ Term(const\ |\ const,\ pow) \] -
Expr.mul:该函数是表达式乘以表达式,相当于一个表达式中的项乘另一个表达式的项,于是调用了Term.mul,将Term.mul的返回值,即下文中的ret直接取出其中最内层的每一个Term加入表达式res中,最后返回res,结构如下:\[(Expr)\ res \rightarrow (many\ Terms)\ Term(const\ |\ const,\ pow) \] -
Term.mul:其实就是先将Term中的不是表达因子的因子乘起来,封装为一个表达式因子,然后又调用表达式的乘法将所有表达式因子乘起来(调用乘法前每个因子注意先调用一遍Expr.expand那么项乘项时就不用先调Term.expand,不然会无限递归,这里可以自行理解一下),最后返回一个叫ret的Term,结构同样如下:\[(Term)\ ret \rightarrow (Expr)\ res \rightarrow (many\ Terms)\ Term(const\ |\ const,\ pow) \]
总之就是四个函数相互递归调用,特别注意每次返回要封装成什么样子,以及搞清楚当前对象里面到底是几层(或无数层),简单来讲就是拆包和装包的问题
-
-
化简:这个就很简单了,两个函数一个对项进行化简,一个对表达式进行化简,都用
HashMap就好,对表达式和项都是<key,val> ---> <index,coefficient>,在上面四个函数返回的时候都调用一次Simplify就好,千万不要expand完再一起化简,这就是为什么有的人(x+1)**25都跑不出来,有的人(x+1)**1000都可以秒出的原因(就是提前减少了容器中的东西,降低了爆栈,遍历超时等可能) -
递归打印:就是每个结构都有一个
toString方法,上层调下层,递归调用即可,与前面那四个函数互调相比简直不要太简单
性能
-
尽可能令第一项为系数为正,省去首项的正号
-
x**2输出为x*x的形式可以省去一个字符 -
合并同类项,即
simplify方法
代码结构分析
类图
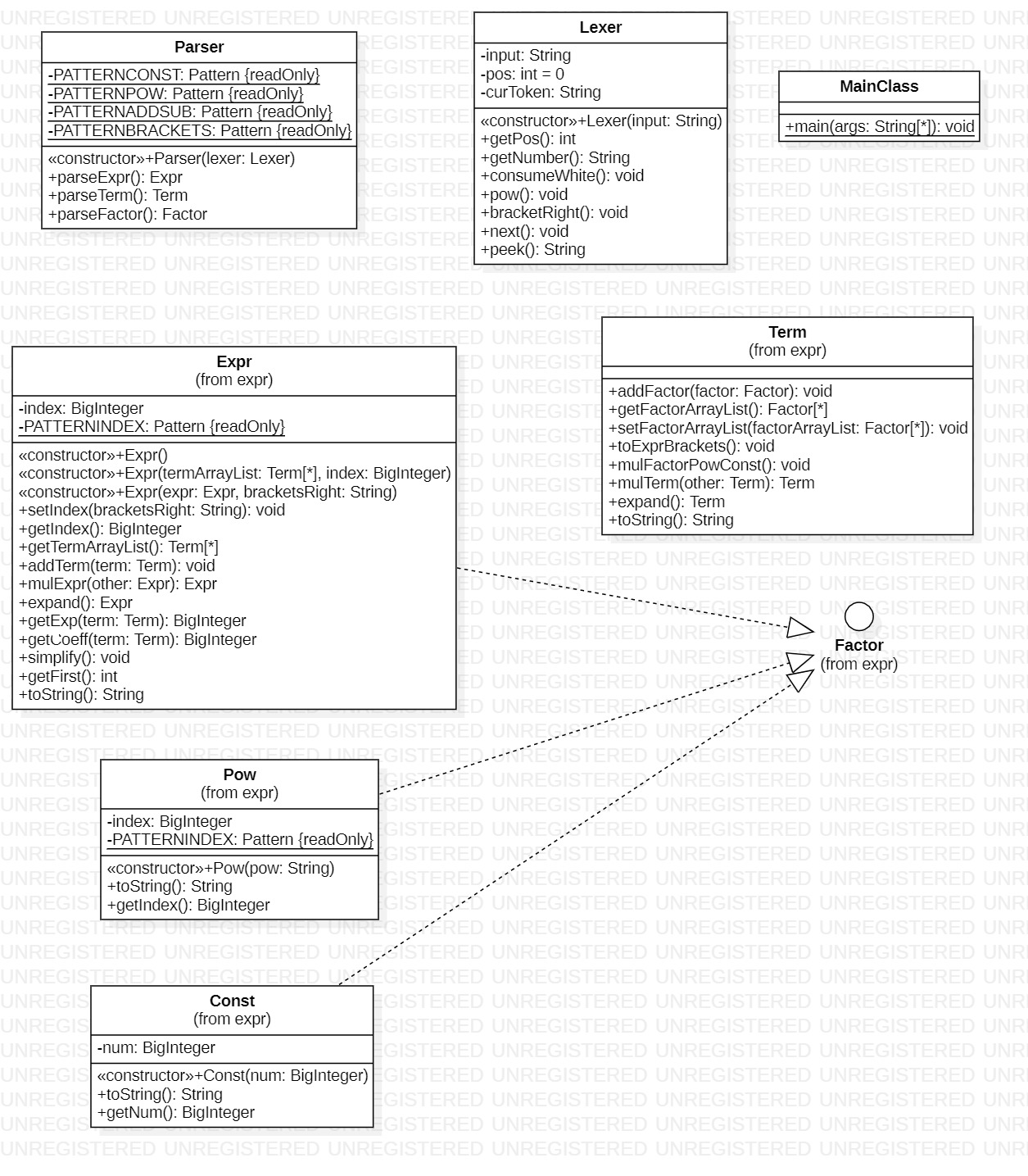
由于是第一次作业,这个类图还是比较简单的吧,其实就是按照作业里面给定的形式化表述建立的结构模型
复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Lexer | 2.88 | 6 | 23 |
| MainClass | 2 | 2 | 2 |
| Parser | 3.75 | 8 | 15 |
| expr.Const | 1.33 | 2 | 4 |
| expr.Expr | 2.64 | 7 | 37 |
| expr.Pow | 2 | 4 | 6 |
| expr.Term | 3.5 | 6 | 28 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.bracketRight() | 10 | 1 | 9 | 9 |
| Lexer.consumeWhite() | 2 | 1 | 2 | 3 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPos() | 0 | 1 | 1 | 1 |
| Lexer.next() | 6 | 2 | 5 | 6 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Lexer.pow() | 10 | 1 | 9 | 9 |
| MainClass.main(String[]) | 2 | 1 | 3 | 3 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 5 | 1 | 5 | 5 |
| Parser.parseFactor() | 13 | 7 | 8 | 8 |
| Parser.parseTerm() | 3 | 1 | 4 | 4 |
| expr.Const.Const(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Const.getNum() | 0 | 1 | 1 | 1 |
| expr.Const.toString() | 1 | 1 | 2 | 2 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.Expr(ArrayList |
0 | 1 | 1 | 1 |
| expr.Expr.Expr(Expr, String) | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.expand() | 1 | 1 | 2 | 2 |
| expr.Expr.getCoeff(Term) | 3 | 1 | 3 | 3 |
| expr.Expr.getExp(Term) | 3 | 1 | 3 | 3 |
| expr.Expr.getFirst() | 15 | 6 | 8 | 9 |
| expr.Expr.getIndex() | 0 | 1 | 1 | 1 |
| expr.Expr.getTermArrayList() | 0 | 1 | 1 | 1 |
| expr.Expr.mulExpr(Expr) | 3 | 1 | 3 | 3 |
| expr.Expr.setIndex(String) | 0 | 1 | 1 | 1 |
| expr.Expr.simplify() | 10 | 3 | 7 | 7 |
| expr.Expr.toString() | 6 | 5 | 4 | 6 |
| expr.Pow.Pow(String) | 0 | 1 | 1 | 1 |
| expr.Pow.getIndex() | 0 | 1 | 1 | 1 |
| expr.Pow.toString() | 3 | 4 | 3 | 4 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.expand() | 6 | 1 | 5 | 5 |
| expr.Term.getFactorArrayList() | 0 | 1 | 1 | 1 |
| expr.Term.mulFactorPowConst() | 5 | 1 | 4 | 4 |
| expr.Term.mulTerm(Term) | 6 | 1 | 5 | 5 |
| expr.Term.setFactorArrayList(ArrayList |
0 | 1 | 1 | 1 |
| expr.Term.toExprBrackets() | 11 | 1 | 5 | 5 |
| expr.Term.toString() | 13 | 1 | 5 | 7 |
可以看到总的来说圈复杂度还是比较低的,可维护性与可测试性还是比较好的,但是几个toString的非结构化程度还是太高,可能这就是熬夜后早起写代码的后果吧,还有几个耦合度过高的方法基本都在Parser,Lexer里面,这也是我为什么第二次开始就将它们中的方法拆开的原因,(太难复用,太难实现增量开发)
测试
- 通过学习室友搞的
Python自动评测机(同样运用递归下降生成表达式,然后将我代码跑出的结果用sympy调整后与sympy展开输入的表达式的结果对比) - 手动根据每个结构构造小的特殊样例。
这次写完后就比较顺利,没发现bug
评测
此次中测、强测、互测均未被Hack且没丢性能分,但我也没有发现任何人bug(其实房间所有人都是0/x),表面上一片祥和,其实这次当我那四个关键函数的递归调用写对后,就没有测出过bug
第二次作业
作业思路
架构
第二次作业是支持sin、cos、sum以及自定义函数,同时允许简单的括号嵌套,但是有诸多限制,如sin、cos中是因子但不允许表达式因子等等。由于第一次已经支持递归调用所以感觉工作量并不是很大,思路同上次不用重构,(但是我把之前判断Wrong Format代码全删了),这次与第一次区别就是:
- 存储结构:引入了
Function抽象类,由Pow、Sin、Cos、DiyFunction、Sum继承同时再让Sin、Cos实现Factor接口 - 递归下降:在
parser时候,就将DiyFunction、Sum用字符串替换展开,直接存储为Expr,Term等等非Function类型的结构,此处替换其实感觉还可以,因为只要替换时,在替换的元素外面加一层括号就绝对不会有事,反正后面expand、mul函数也会进行拆包 - 展开括号:基本和上次一样,除了
sin、cos由于我支持了内部是表达式因子,于是我发现因子是三角函数且内部是一个表达式因子就要进去展开,化简,如果还是一个sin、cos那么继续往里面搜索 - 化简:这方面则是大改了一下:
- Term:运用
HashMap化简,结构是<key, val> ---> <Factor, index>,这里的Factor并不是项中的每一个因子,而是每一个因子的基本单元,例如sin(1)、sin(x**2)、x**3的基本单元就是sin(1)、sin(x**2)、x,如果基本单元一样,就将指数index相加进行合并,所以我对Factor写了一个getBase方法由每个类去实现 - Expr:重写了每一个类的
hashCode和equals方法,建立一个Hash套Hash的结构,即HashMap<HashSet<Factor>, coefficient>的结构,其中的key就是Term的每一个因子组成的HashSet,val就是Term的系数(Term中的常数因子已经合并到系数中去了)
- Term:运用
- 递归打印:这个思路和上次一样,但是上次作业的这个部分一堆特判,并且逻辑凌乱,这次全部重写了
性能
相比于上次:
- 将
cos里面常数的符号去掉,sin的符号全部提到外部,由于中间出了点小问题于是没有做sin、cos的平方化简 cos(0),sin(0)输出\(1\)和\(0\)
代码结构分析
类图

明显比上次复杂多了,这一次增加了一个Function父类,使结构更加清晰明了,同时如果要加新功能直接添加一个类继承Function就好了(也是根据作业的形式化表述学到的。。。),虽然Parser,Lexer里面增加了一大堆函数,但其实是改变了之前每个函数功能不明确,实现及其混乱的情况,而现在虽然函数多了,但是功能清晰,非常便于阅读
复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Lexer | 2.4 | 10 | 24 |
| MainClass | 1.5 | 2 | 3 |
| Parser | 2.06 | 8 | 33 |
| expr.Const | 1.33 | 3 | 8 |
| expr.Cos | 2.57 | 5 | 18 |
| expr.DiyFunction | 4.5 | 5 | 9 |
| expr.Expr | 2.12 | 8 | 34 |
| expr.Function | 1.25 | 2 | 5 |
| expr.Pow | 2 | 4 | 10 |
| expr.Sin | 2.71 | 6 | 19 |
| expr.Sum | 2 | 3 | 4 |
| expr.Term | 2.64 | 9 | 37 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getBracketRight() | 6 | 1 | 5 | 5 |
| Lexer.getCos() | 0 | 1 | 1 | 1 |
| Lexer.getDiyFunction() | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPow() | 6 | 1 | 5 | 5 |
| Lexer.getSin() | 0 | 1 | 1 | 1 |
| Lexer.getSum() | 0 | 1 | 1 | 1 |
| Lexer.next() | 11 | 2 | 11 | 12 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| MainClass.parse(String) | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.getConst() | 1 | 1 | 2 | 2 |
| Parser.getCos() | 0 | 1 | 1 | 1 |
| Parser.getDiyFunction() | 1 | 1 | 2 | 2 |
| Parser.getExpr() | 0 | 1 | 1 | 1 |
| Parser.getExpr(String) | 0 | 1 | 1 | 1 |
| Parser.getFactor() | 0 | 1 | 1 | 1 |
| Parser.getPow() | 0 | 1 | 1 | 1 |
| Parser.getSin() | 0 | 1 | 1 | 1 |
| Parser.getSum() | 0 | 1 | 1 | 1 |
| Parser.getSumFactor() | 6 | 1 | 4 | 5 |
| Parser.getTerm(String) | 0 | 1 | 1 | 1 |
| Parser.getTermSign() | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 4 | 1 | 5 | 5 |
| Parser.parseFactor() | 8 | 8 | 9 | 9 |
| Parser.parseTerm() | 3 | 1 | 4 | 4 |
| expr.Const.Const(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Const.equals(Object) | 3 | 3 | 2 | 4 |
| expr.Const.getBase() | 0 | 1 | 1 | 1 |
| expr.Const.getNum() | 0 | 1 | 1 | 1 |
| expr.Const.hashCode() | 0 | 1 | 1 | 1 |
| expr.Const.toString() | 0 | 1 | 1 | 1 |
| expr.Cos.Cos(Factor, String) | 3 | 1 | 3 | 4 |
| expr.Cos.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Cos.expand() | 13 | 1 | 5 | 5 |
| expr.Cos.getBase() | 0 | 1 | 1 | 1 |
| expr.Cos.getFactor() | 0 | 1 | 1 | 1 |
| expr.Cos.hashCode() | 0 | 1 | 1 | 1 |
| expr.Cos.toString() | 4 | 3 | 3 | 4 |
| expr.DiyFunction.addDiyFunction(String) | 6 | 1 | 5 | 5 |
| expr.DiyFunction.substituteInto(String, ArrayList |
4 | 1 | 3 | 4 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.Expr(ArrayList |
0 | 1 | 1 | 1 |
| expr.Expr.Expr(Expr, String) | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Expr.expand() | 1 | 1 | 2 | 2 |
| expr.Expr.expandIndex() | 1 | 1 | 2 | 2 |
| expr.Expr.getBase() | 0 | 1 | 1 | 1 |
| expr.Expr.getFirst() | 3 | 3 | 3 | 3 |
| expr.Expr.getIndex() | 0 | 1 | 1 | 1 |
| expr.Expr.getTermArrayList() | 0 | 1 | 1 | 1 |
| expr.Expr.hashCode() | 0 | 1 | 1 | 1 |
| expr.Expr.mulExpr(Expr) | 3 | 1 | 3 | 3 |
| expr.Expr.setIndex(String) | 1 | 1 | 2 | 2 |
| expr.Expr.simplify() | 4 | 1 | 3 | 3 |
| expr.Expr.toString() | 8 | 4 | 5 | 8 |
| expr.Function.calculate(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Function.getBase() | 0 | 1 | 1 | 1 |
| expr.Function.getIndex() | 0 | 1 | 1 | 1 |
| expr.Function.setIndex(String) | 1 | 1 | 2 | 2 |
| expr.Pow.Pow(String) | 0 | 1 | 1 | 1 |
| expr.Pow.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Pow.getBase() | 0 | 1 | 1 | 1 |
| expr.Pow.hashCode() | 0 | 1 | 1 | 1 |
| expr.Pow.toString() | 3 | 4 | 3 | 4 |
| expr.Sin.Sin(Factor, String) | 4 | 1 | 4 | 5 |
| expr.Sin.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Sin.expand() | 18 | 1 | 6 | 6 |
| expr.Sin.getBase() | 0 | 1 | 1 | 1 |
| expr.Sin.getFactor() | 0 | 1 | 1 | 1 |
| expr.Sin.hashCode() | 0 | 1 | 1 | 1 |
| expr.Sin.toString() | 4 | 3 | 3 | 4 |
| expr.Sum.Sum(BigInteger, BigInteger, String) | 0 | 1 | 1 | 1 |
| expr.Sum.expand() | 2 | 2 | 2 | 3 |
| expr.Term.Term() | 0 | 1 | 1 | 1 |
| expr.Term.Term(BigInteger, HashSet |
0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.delConst() | 4 | 1 | 3 | 3 |
| expr.Term.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Term.expand() | 14 | 1 | 11 | 13 |
| expr.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| expr.Term.getFactorArrayList() | 0 | 1 | 1 | 1 |
| expr.Term.hashCode() | 0 | 1 | 1 | 1 |
| expr.Term.mulTerm(Term) | 7 | 1 | 6 | 6 |
| expr.Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Term.setFactorArrayList(ArrayList |
0 | 1 | 1 | 1 |
| expr.Term.simplify() | 5 | 1 | 4 | 4 |
| expr.Term.toString() | 5 | 2 | 5 | 5 |
修改了Parser和Lexer之后它们中的方法的复杂度比上次好多了,除了Lexer.next(),Parser.parseFactor(),但是我也不太知道他们为什么圈复杂度变高了,其实我感觉这次他应该更好维护,更加清晰了,可能是else if太多(不过感觉这样反而逻辑清晰)。。。
当然此次最大的问题就是Term.expand(),sin.expand()模块设计复杂度和圈复杂度过高,其实我自己也知道这次它们两个写的很差,因为条件判断写的过于繁琐,有好几处过于杂糅,但是以我的水平好像不得不这么写。。。
虽然看上去总的高内聚低耦合程度比第一次差了一些,但是由于加了不少新东西,我认为还是比第一次处理得更加自然与熟练
测试
基本同上次,就改了改对拍机,通过向std和src的结果输入100个数据,计算表达式代入数据后的结果对比评测。
至于上面说的这次中间出的小问题就是,我的对拍机造了一组数据输出大概在72.7kb左右,但我的输出少了好多只有13kb(优化性能也不至于这么短吧。。。),于是版本回退找bug,结果发现是由于我读到sin(0)、cos(0)就返回一个const(0)、const(1),只要删掉这里就是对的了,但是当时不知道为什么于是也不敢再接着优化缩短长度了,只想着用什么方法替代上述的替换,最后就是得到最终的表达式的结果后直接正则将sin(0)、cos(0)替换为(0)、(1)再解析一遍
最后再第三次作业中由于三角函数支持嵌套多层了,无法用正则替换,所以发现了其实是我在解析替换时没有考虑指数的情况即sin(0)**0我检测到sin内部是0就直接扔掉该因子,将其替换为0了,非常愚蠢。。。
评测
此次同样中测,强测,互测均未被Hack,不过由于未作平方优化丢了\(5\)分性能分,但是好在发现了他人的bug:
- 对于
sin(-5)**2这种无脑将-提到外面,不考虑一下指数,属于是和我上面不考虑指数直接替换一样了,不过我恰好发现并规避了那个问题
第三次作业
作业思路
架构
可以说除了化简,提括号部分加了几个函数,完全没动,非常滑水(当然还直面了第二次作业的那个小问题。。。)
-
化简:
-
三角平方和化简:简单介绍一下思路就是,会得到三个表达式,一个是原始化简后的表达式,一个是将所有符合:
\[sin(Factor)^k\times Term\ \ (k\ge 2) \]的项换为:
\[(1-cos(Factor)^2)\times sin(Factor)^{k-2}\times Term \]的表达式,还有一个是换
cos得到的表达式,方法同上,将第一个表达式与后两个表达式再解析后的toString字符串比较长短,选取最短的作为结果,注意考虑到运行时间以及效率,要换就将所有能换的sin,或者所有能换的cos一起换掉,并且如果指数大于\(4\),也只换一次,即可能换完后三角的指数剩余还是大于\(2\)我也不再换了,注意在三角的展开化简时候也要对里面的表达式进行操作,该过程是递归的 -
将三角函数最内层正负号取出或扔掉:这是在
parse的时候做的:- sin:如果其内部的因子是常数的情况在第二次作业已经考虑,这里只说如果是表达式这么办,首先在
parse时候就将三角函数内的表达式进行展开化简,由于我是找一个正的项放在表达式最前面(优化性能),因此只要检测这个表达式的第一项的符号就好,如果是-的,证明该表达式找不到一个正的项,每一项都是负的,这时在考虑一下指数奇偶决定是直接每一项取反还是还要将负号提到sin外面,该过程同样是递归的 - cos:同上,就是不用考虑指数,无脑去项的负号即可
- sin:如果其内部的因子是常数的情况在第二次作业已经考虑,这里只说如果是表达式这么办,首先在
-
性能
相比于上次:
- 三角平方化简
- 三角内部符号提出到最外层(上次只做了三角内部只有一个常数的情况,这次考虑到内部多层嵌套,以及表达式符号提出问题)
代码结构分析
类图
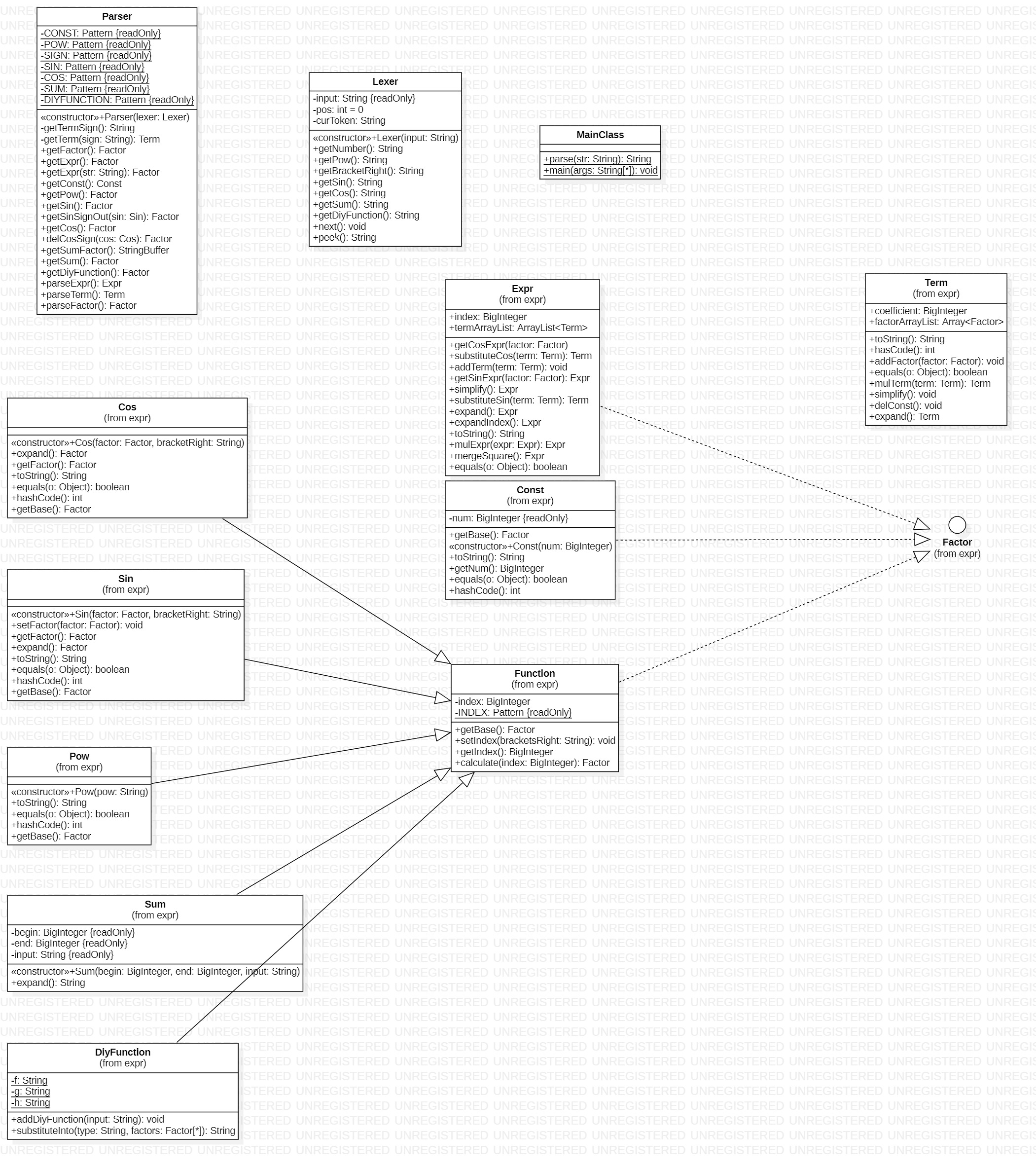
除了Expr,Parser,中的多了几个化简相关的方法其它完全一致
复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Lexer | 2.4 | 10 | 24 |
| MainClass | 1.5 | 2 | 3 |
| Parser | 2.44 | 8 | 44 |
| expr.Const | 1.33 | 3 | 8 |
| expr.Cos | 3.14 | 9 | 22 |
| expr.DiyFunction | 4.5 | 5 | 9 |
| expr.Expr | 2.3 | 8 | 46 |
| expr.Function | 1.25 | 2 | 5 |
| expr.Pow | 2 | 4 | 10 |
| expr.Sin | 3 | 10 | 24 |
| expr.Sum | 2 | 3 | 4 |
| expr.Term | 2.64 | 9 | 37 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getBracketRight() | 6 | 1 | 5 | 5 |
| Lexer.getCos() | 0 | 1 | 1 | 1 |
| Lexer.getDiyFunction() | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPow() | 6 | 1 | 5 | 5 |
| Lexer.getSin() | 0 | 1 | 1 | 1 |
| Lexer.getSum() | 0 | 1 | 1 | 1 |
| Lexer.next() | 11 | 2 | 11 | 12 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| MainClass.parse(String) | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.delCosSign(Cos) | 4 | 1 | 4 | 4 |
| Parser.getConst() | 1 | 1 | 2 | 2 |
| Parser.getCos() | 1 | 1 | 2 | 2 |
| Parser.getDiyFunction() | 1 | 1 | 2 | 2 |
| Parser.getExpr() | 0 | 1 | 1 | 1 |
| Parser.getExpr(String) | 0 | 1 | 1 | 1 |
| Parser.getFactor() | 0 | 1 | 1 | 1 |
| Parser.getPow() | 0 | 1 | 1 | 1 |
| Parser.getSin() | 1 | 1 | 2 | 2 |
| Parser.getSinSignOut(Sin) | 10 | 3 | 8 | 8 |
| Parser.getSum() | 0 | 1 | 1 | 1 |
| Parser.getSumFactor() | 6 | 1 | 4 | 5 |
| Parser.getTerm(String) | 0 | 1 | 1 | 1 |
| Parser.getTermSign() | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 4 | 1 | 5 | 5 |
| Parser.parseFactor() | 8 | 8 | 9 | 9 |
| Parser.parseTerm() | 3 | 1 | 4 | 4 |
| expr.Const.Const(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Const.equals(Object) | 3 | 3 | 2 | 4 |
| expr.Const.getBase() | 0 | 1 | 1 | 1 |
| expr.Const.getNum() | 0 | 1 | 1 | 1 |
| expr.Const.hashCode() | 0 | 1 | 1 | 1 |
| expr.Const.toString() | 0 | 1 | 1 | 1 |
| expr.Cos.Cos(Factor, String) | 3 | 1 | 3 | 4 |
| expr.Cos.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Cos.expand() | 15 | 2 | 10 | 11 |
| expr.Cos.getBase() | 0 | 1 | 1 | 1 |
| expr.Cos.getFactor() | 0 | 1 | 1 | 1 |
| expr.Cos.hashCode() | 0 | 1 | 1 | 1 |
| expr.Cos.toString() | 4 | 3 | 3 | 4 |
| expr.DiyFunction.addDiyFunction(String) | 6 | 1 | 5 | 5 |
| expr.DiyFunction.substituteInto(String, ArrayList |
4 | 1 | 3 | 4 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.Expr(ArrayList |
0 | 1 | 1 | 1 |
| expr.Expr.Expr(Expr, String) | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Expr.expand() | 1 | 1 | 2 | 2 |
| expr.Expr.expandIndex() | 1 | 1 | 2 | 2 |
| expr.Expr.getBase() | 0 | 1 | 1 | 1 |
| expr.Expr.getCosExpr(Factor) | 0 | 1 | 1 | 1 |
| expr.Expr.getFirst() | 3 | 3 | 3 | 3 |
| expr.Expr.getSinExpr(Factor) | 0 | 1 | 1 | 1 |
| expr.Expr.getTermArrayList() | 0 | 1 | 1 | 1 |
| expr.Expr.hashCode() | 0 | 1 | 1 | 1 |
| expr.Expr.mergeSquare() | 5 | 1 | 3 | 5 |
| expr.Expr.mulExpr(Expr) | 3 | 1 | 3 | 3 |
| expr.Expr.setIndex(String) | 1 | 1 | 2 | 2 |
| expr.Expr.simplify() | 4 | 1 | 3 | 3 |
| expr.Expr.substituteCos(Term) | 5 | 1 | 4 | 4 |
| expr.Expr.substituteSin(Term) | 5 | 1 | 4 | 4 |
| expr.Expr.toString() | 8 | 4 | 5 | 8 |
| expr.Function.calculate(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Function.getBase() | 0 | 1 | 1 | 1 |
| expr.Function.getIndex() | 0 | 1 | 1 | 1 |
| expr.Function.setIndex(String) | 1 | 1 | 2 | 2 |
| expr.Pow.Pow(String) | 0 | 1 | 1 | 1 |
| expr.Pow.equals(Object) | 3 | 3 | 2 | 4 |
| expr.Pow.getBase() | 0 | 1 | 1 | 1 |
| expr.Pow.hashCode() | 0 | 1 | 1 | 1 |
| expr.Pow.toString() | 3 | 4 | 3 | 4 |
| expr.Sin.Sin(Factor, String) | 4 | 1 | 4 | 5 |
| expr.Sin.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Sin.expand() | 20 | 2 | 12 | 13 |
| expr.Sin.getBase() | 0 | 1 | 1 | 1 |
| expr.Sin.getFactor() | 0 | 1 | 1 | 1 |
| expr.Sin.hashCode() | 0 | 1 | 1 | 1 |
| expr.Sin.setFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Sin.toString() | 4 | 3 | 3 | 4 |
| expr.Sum.Sum(BigInteger, BigInteger, String) | 0 | 1 | 1 | 1 |
| expr.Sum.expand() | 2 | 2 | 2 | 3 |
| expr.Term.Term() | 0 | 1 | 1 | 1 |
| expr.Term.Term(BigInteger, HashSet |
0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.delConst() | 4 | 1 | 3 | 3 |
| expr.Term.equals(Object) | 4 | 3 | 3 | 5 |
| expr.Term.expand() | 14 | 1 | 11 | 13 |
| expr.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| expr.Term.getFactorArrayList() | 0 | 1 | 1 | 1 |
| expr.Term.hashCode() | 0 | 1 | 1 | 1 |
| expr.Term.mulTerm(Term) | 7 | 1 | 6 | 6 |
| expr.Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Term.setFactorArrayList(ArrayList |
0 | 1 | 1 | 1 |
| expr.Term.simplify() | 5 | 1 | 4 | 4 |
| expr.Term.toString() | 5 | 2 | 5 | 5 |
第二次的问题还是一如既往甚至指标又升了一点,因为基本没动它们(怕屎山塌方。。。),不过新加的几个函数,比如说Expr.substituteCos()、.Expr.mergeSquare()...还是处理的比较好的,耦合度都比较低
测试
同上次基本没什么变化,就对拍机调调参数就好了
不过写完后还是发现了一个小bug,就是我有一个函数新建一个Term的时候忘记把之前Term的coefficient赋给它了,用自动对拍机发现问题后还是de了挺久,但其实只是一个粗心的bug
评测
此次还是中测,强测,互测均未被Hack,虽然做了平方优化可由于未做二倍角优化又送了\(3\)分,好在也发现了他人的bug:
sum函数,循环变量没有用BigInteger,被我一波直接带了\(4\)个人,主要是就下了一个人代码,一眼就看到他在sum代入时直接BigInteger.intValue,于是他连带其它\(3\)个兄弟直接被我送走。。。- 还是
sum,有一个兄弟对于\(sum(i, 0, 9, i^2)\)这个表达式,直接就换成\(1^2+2^2+...+9^2\),所以化简时候就错了(之后又没有定义常数的乘方运算),所以替换时应该都带一层括号,比如\((1)^2+(2)^2+...+(9)^2\),这样化简就绝对不会有问题
心得体会与收获
- 本单元感觉自己经过三次作业的洗礼暴露出我非常多的缺陷:虽然每一次都没有重构,但是从第一次到第二次还是改了好多函数,没有做到老师上课说的你写过的代码就不要删了,最好是只在上面加功能,其实就是自己写代码时没有前瞻性同时一些基本的设计模式没有好好遵守,比如三次作业没有一次使用了工厂模式,加功能就非常不方便,需要动以前的代码,这估计也与我经验不足以及每次写代码前习惯没有完全思考清楚只是突然灵感来了就简单想想就开动有关吧。希望在接下来的几次作业中自己可以做到完全想清楚了再写代码并且尽可能按照一些基本的设计模式完成作业
- 虽然缺点暴露很多,但是我同时也收获到了不少东西:
- 优雅的代码:从每次作业的递进,我或多或少都会修改之前的代码,
hw1时写完后感觉写的不错,hw2时看自己hw1的代码却感觉这是我写的吗,怎么这么丑,于是又进行不断的修改,最终慢慢发现应该怎么写才是最优雅的,到了hw3,hw2写的基本就没动了。 - 技能get:
hw1开始学习了递归下降,当时觉得尽然有如此神奇的东西,但是花了大量时间学完后发现它就像呼吸一样自然,还有hw1那四个递归调用让我深刻的认识到封装(装包、拆包)的重要性,最后就是一堆化简上的奇技淫巧(离不开舍友的帮助),让我更加熟练了对一些基本数据结构的使用,比如:HashMap、HashSet。。。 - 心理上:提高了自己的抗压能力与意志力,我应该会一直记得第一次作业那个周五晚上,展开的那四个函数的递归调用一直出错(死循环、拆包装包不对),甚至是整个代码框架都因为它们四个而乱套,一度有了重开的想法,差点就删库了,好在与舍友一番讨论之后思路逐渐清晰,该删就删,该加就加,终于写到凌晨3点写完了它们,但是还有
toString没写,并且还不知道又没有bug(虽然都进行了简单的单元测试,但是还是不放心,当然后来证明我在熬夜时竟然没出bug)于是第二天早上7点又爬起来继续写(非常难受)。 - 妥协:几次作业其实自己都有一些不切实际(其实是菜)的想法,当然最后都没有实现或者已经实现成为另一个样子了,最后迫不得已只能接收了(比如第三次的化简,就算是平方和我也没有将它们化到极致,而是采取了一定的策略),这也让我明白了想十全十美是不可能的,就算是写的不好或是不太会写的优美也要硬着头皮上,不然可能
ddl就过了。。。
- 优雅的代码:从每次作业的递进,我或多或少都会修改之前的代码,
一些建议
- 其实感觉从第二次到第三次感觉课程组应该是放水了,希望可以在让我感受一下
hw1时凌晨3点的滋味,以及希望这3个难度是递进关系,目前来看其实第一次作业最难,第二次差一点,第三次过水 - 感觉可以多介绍一点设计模式相关的东西,因为就从互测同学的代码来看基本上所有人与我差不多都没有这方面的概念,有的也只是简单用了一点工厂模式,但是感觉其实用的可能也不算太好,感觉多介绍一点这方面的知识可以提高我们写程序的可维护性与拓展性,而不是每次都重构或者修改之前的代码
好了,第一单元完结撒花,最后希望我有个美好的第二单元,虽然不太现实。。。


