NOI2025 D1T3 数字树 (tree) 题解

NOI 2025 折戟沉沙！

给定一棵 \(4n - 1\) 个节点的 二叉树，其中每个非叶节点都有 恰好 两个子节点。

非叶节点编号为 \(1\sim 2n - 1\)，叶子节点编号为 \(2n\sim 4n - 1\)。

初始时，每个叶子节点上都没有数字。

定义一个 DFS 序是优美的，当且仅当按该 DFS 序将所有 标有数字的叶子节点 上的数字拼成一个序列时，可以通过若干次 消除相邻相同数字 的方式删空。

给定 \(n\) 次操作，第 \(i\) 操作会选择两个 没有数字 的叶子节点 \(a_i,b_i\)，然后将这两个节点标上数字 \(i\)。

• 保证在每次操作后，存在至少一个优美的 DFS 序。

你需要求出每次操作后的优美的 DFS 序的数量，对 \(10^9+7\) 取模。

\(1\le n\le 2\times 10^5\)​

• 部分分（特殊性质）：保证 \(a_i,b_i\) 位于根节点 \(1\) 的不同子树中。

• 提示：观察发现大样例中所有答案中的数都形如 \(2^k\)，其中 \(k\le 2n-1\)。

---

下面结论来自国家集训队 rk.9 hhoppitree，太大神。

最开头给出结论：

定义一个点的权值为：子树内恰好出现过一次的数形成的集合。

设 \(C_i\) 表示第 \(i\)​ 次所有本质不同的权值个数。

则第 \(i\) 次答案为 \(2^{2n+i-C_i}\)。

如果懒得看证明可以直接跳到最后看如何维护。

---

不同 DFS 序能通过翻转 \(2n-1\) 个子树中的某些一一对应，下面考虑翻转子树。

根据提示，容易往某些方面想：比如找到一些相对独立的子树翻转的限制，那么答案就是 \(2^{\text{限制个数}}\)。

经典套路：由于保证存在优美的 DFS 序，我们不妨设最开始的树的 DFS 序是满足条件的，然后去挖性质。

否则容易交换一些左右儿子调整成这样。

---

先考虑特殊性质。最终答案能删空的串一定形如：\(\color{pink}{14322341}\)​ 这样。

• 子树等价于某个 DFS 序区间，拍平后性质更多，后面都用区间去叙述。

因为所有的点对都是经过根的，所以翻转了一段 DFS 序区间，就需要对应地翻转右边内容完全一样的区间！

• 其中内容定义为区间恰好出现过一次的数形成的集合。

由于所有区间的内容形成了若干等价类，因此上述限制等价于：每个等价类必须恰好选择偶数个区间翻转。

• 简单点说等价类：就是相同权值的点在一个等价类内。

---

但是这东西有点小问题：翻转集合大小 \(\le 1\) 的区间没有意义，重写得严谨些：

上述限制等价于：每个内容里 \(>1\)​ 个元素的等价类必须恰好选择偶数个区间翻转。

我们发现大小为 \(0\) 的等价类共 \(1\) 个，第 \(i\) 次会有 \(i\) 个大小为 \(1\)​ 的等价类个数。

总共有 \(2n-1\) 个非叶子可以翻转。

于是设 \(C_i\) 表示第 \(i\) 次所有子树的形成的等价类个数。

由于每个必须恰好选择偶数个区间翻转的限制会使得方案数 \(/2\)，于是第 \(i\)​ 次答案为：

\[2^{2n-1-(C_i-i-1)}=2^{2n+i-C_i} \]

---

如果没有特殊性质是否也一样呢？

考虑根的两个子树，它们中有一些跨越根的和完全在内部的数字对。

对于任何一个点的子树，分析时只保留恰出现一次的数字，而忽略其它的。

如果只有跨过根的数字，和特殊性质的分析完全一致。

一个子树如果既包含跨越根的数字，又打乱了一些完全在内部的数字对，就一定要翻转偶数次。

这个结论可以反证：找到最上面的翻转了奇数次的子树，没有其它子树能救它，就一定不合法。

我们保留了只有完全在内部的数字对的情况，因此可以递归进根的两个子树各自分析。

于是我们证明了这个结论仍然成立！

---

于是我们只需要求等价类个数：\(C_1,C_2,\cdots ,C_n\)​​。

本题后半部分和 qoj 5425——Proposition Composition 有点类似。

转换下参考对象，对每个数 \(i\) 刻画其在哪些子树出现过。

于是对 \(1\sim 4n-1\) 中的每个节点 \(i\) 记录字符串 \(s_i\)，其中 \(s_{i,j}=1\) 表示 \(i\) 子树内 \(j\) 是否恰好出现一次​​。

上个图：

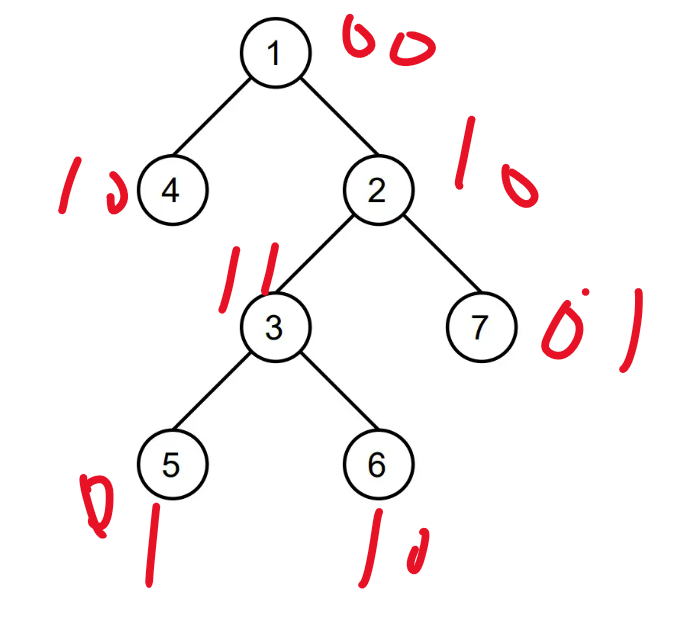
字符串数组 \(s\) 是容易线段树合并维护的，合并的时候做个 \(\text{xor}\)。

不难发现 \(x\) 和 \(y\) 位置等价的时刻是 \([1,\text{lcp}(s_x,x_y)]\) 这个区间​。

然后类似 SA 中 height 数组那类做法，我们排序所有 \(s\)，排序成 \(S\)​。

求出相邻两两的 \(d_x=\text{lcp}(S_x,S_{x+1})\)，容易发现第 \(i\) 次等价类个数就是 \(d_x<i\) 的个数再 \(+1\)​，随便前缀和一下。

为啥等价类个数是这个呢？大概就是排序后能表示所有大小相邻的不等价类，再 \(+1\) 就是等价类个数。

xor hash 维护等价类，排序和 \(\text{lcp}\)​ 直接线段树二分即可，记得开 unsigned long long。

时间复杂度 \(\mathcal{O}(n\log^2 n)\)，空间 \(\mathcal{O}(n\log n)\)。常数不要太大都足以通过。

---

官方题解说了个不一定跑得过 \(\log^2\) 的单 \(\log\)，讲一下。

注意到瓶颈在于最后的字典序排序，考虑优化。

发现只需将线段树合并中所有的 \(\mathcal{O}(n \log n)\) 个节点排序即可！

以每个节点的左右儿子的字典序为第 \(1,2\) 关键字，进行基数排序即可。

为了方便实现，把线段树长度补成 \(2\) 的次幂，从线段树的叶子（区间长度为 \(1\)）开始做，每次给一层排序。

时空复杂度均为 \(\mathcal{O}(n \log n)\)​，足以通过。

其实感觉也没有特别难写，不过我不写

个人感觉有点像后缀平衡树，或者 P6272 没有人的算术？但是貌似没几个和我一样想的。

---

官方题解一个很唐的地方，是没有发现第 \(i\) 次恰好有 \(i\) 个大小为 \(1\) 的等价类。

我这样能直接算等价类个数，最后 \(-i\)​ 即可，比官方做法好写一万倍。

• 官方题解是真的算了大小 \(>1\) 的等价类个数，还要线段树多维护好多东西。

虽然归并排序 stable_sort 的比较次数 \(<\) 快速排序 sort 的比较次数，但是实际上 sort 跑得更快？有点神秘。

下面是 \(\log^2\) 实现，代码非常非常短，跑挺快的：

// 洛谷 P13273
// https://www.luogu.com.cn/problem/P13273
#include<bits/stdc++.h>
#define LL long long
#define u64 unsigned long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
mt19937_64 rnd(time(0));
const int N=8e5+5,M=4e7+5,mod=1e9+7;
int n,m,K,tt,p2[N],rt[N],p[N],s[N];
array<int,2>so[N];
inline int md(int x){return x>=mod?x-mod:x;}
struct node{int ls,rs;u64 x;}a[M];
#define ls(w) a[w].ls
#define rs(w) a[w].rs
inline void pu(int w){a[w].x=a[ls(w)].x^a[rs(w)].x;}
void upd(int &w,int p,u64 x,int l=1,int r=n)
{
	if(!w) w=++tt;a[w].x^=x;
	if(l==r) return;int m=(l+r)>>1;
	p<=m?upd(ls(w),p,x,l,m):upd(rs(w),p,x,m+1,r);
}
int mg(int x,int y,int l=1,int r=n)
{
	if(!x||!y) return x|y;int z=++tt;
	if(l==r) return a[z].x=a[x].x^a[y].x,z;
	int m=(l+r)>>1;
	return a[z].x=a[ls(z)=mg(ls(x),ls(y),l,m)].x^
		   		  a[rs(z)=mg(rs(x),rs(y),m+1,r)].x,z;
}
bool cmp(int x,int y,int l=1,int r=n)
{
	if(!x) return 1;if(!y) return 0;
	if(l==r) return a[x].x<a[y].x;int m=(l+r)>>1;
	if(a[ls(x)].x==a[ls(y)].x) return cmp(rs(x),rs(y),m+1,r);
	return cmp(ls(x),ls(y),l,m);
}
int lcp(int x,int y,int l=1,int r=n)
{
	if(a[x].x==a[y].x) return r-l+1;
	if(l==r) return 0;int m=(l+r)>>1;
	if(a[ls(x)].x==a[ls(y)].x) return m-l+1+lcp(rs(x),rs(y),m+1,r);
	return lcp(ls(x),ls(y),l,m);
}
void dfs(int x){
	auto [u,v]=so[x];
	if(x<m) dfs(u),dfs(v),rt[x]=mg(rt[u],rt[v]);
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>n;
	m=2*n;K=4*n-1;for(int i=*p2=1;i<=m;i++) p2[i]=md(p2[i-1]<<1);
	for(int i=1,x,y;i<m;i++) cin>>x>>y,so[i]={x,y};u64 z;
	for(int i=1,x,y;i<=n;i++)
		cin>>x>>y,z=rnd(),upd(rt[x],i,z),upd(rt[y],i,z);
	dfs(1);for(int i=1;i<=K;i++) p[i]=rt[i];
	sort(p+1,p+1+K,[&](int x,int y){return cmp(x,y);});
	for(int i=1;i<K;i++) s[lcp(p[i],p[i+1])]++;
	for(int i=1;i<=n;i++) s[i]+=s[i-1];
	for(int i=1;i<=n;i++) cout<<p2[m+i-s[i-1]-1]<<"\n";
	return 0;
}