【题解】 APIO2009 会议中心

MADE BY P.Y.Y

作为本官方博客的第一篇题解的作者，P.Y.Y同志表示内心还是有点小紧张的......

不过这也算是本蒟蒻的抛砖引玉吧！

如果大家觉得有写的不好/不清楚的地方可以在下方留言或私Q我，我会尽量改进的！

首先是题面传送门

Siruseri 政府建造了一座新的会议中心。许多公司对租借会议中心的会堂很感兴趣，他们希望能够在里面举行会议。

对于一个客户而言，仅当在开会时能够独自占用整个会堂，他才会租借会堂。会议中心的销售主管认为：最好的策略应该是将会堂租借给尽可能多的客户。

显然，有可能存在不止一种满足要求的策略。例如下面的例子。总共有 4 个公司。他们对租借会堂发出了请求，并提出了他们所需占用会堂的起止日期（如下表所示）。

       开始日期 结束日期 
 公司1    4        9 
 公司2    9        11 
 公司3    13       19 
 公司4    10       17

上例中，最多将会堂租借给两家公司。租借策略分别是租给公司 1 和公司 3，或是公司 2 和公司 3，也可以是公司 1 和公司 4。注意会议中心一天最多租借给一个公司，所以公司 1 和公司 2 不能同时租借会议中心，因为他们在第九天重合了。

销售主管为了公平起见，决定按照如下的程序来确定选择何种租借策略：首先，将租借给客户数量最多的策略作为候选，将所有的公司按照他们发出请求的顺序编号。对于候选策略，将策略中的每家公司的编号按升序排列。最后，选出其中字典序最小的候选策略作为最终的策略。

例中，会堂最终将被租借给公司 1 和公司 3：3 个候选策略是 {(1,3),(2,3),(1,4)}。而在字典序中(1,3)<(1,4)<(2,3)。你的任务是帮助销售主管确定应该将会堂租借给哪些公司。

其实我们可以将这个题抽象成一张图

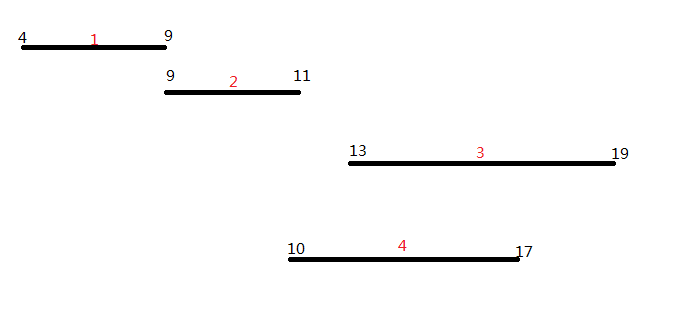
（图中也就是样例其中红色的数字是线段编号黑色的数字的线段左、右端点对应的的位置）

我们要选出尽量多条不重合的线段，并保证字典序最小

可以轻易看出我们最多可以选择2条线段选择的方案有：{1，3} {1，4}{2，3}

但题目要求的字典序最小那么答案就是{1，3}了

如果只需要求第一问的话，我们可以轻易地求出答案（按 r 大小排序然后贪心就可以了）

但是这题没有那么简单！它要求求出字典序最小的最优选择方案这也是这题的精（du）妙（liu）之处

我们发现我们按排序贪心出的答案，虽然总的线段数是正确的，但是它不一定是字典序最小的答案，这就很令人头大

考虑一条线段如果它是答案的话，把它加入答案集合，是不会影响能取到的线段总数的

（线段[L1,R1]和线段[L2,R2]是当前答案集合中，左边和右边离区间[L,R]最近的两个，且一定不与当前线段有重合的部分）

如图如果线段[L，R]属于我们要求的答案集合加入线段[L,R]的话，是不会对整体答案产生影响的，因为其不会L1之前的和R2之后的区间产生影响（想一下，如果能够影响这些区间的话，说明我们选择的这个线段与这些区间有重合的部分，而这种情况是不可能存在的），我们可以缩小一下范围，对于(R1,L2)而言，答案也不会产生影响。

于是，我们可以按字典序枚举一下所有的线段如果所加入的线段不与任何一条已有的线段有重合 且不会对答案产生影响 那么我们就把它加入答案（实际上直接输出该线段的编号就好啦~

这里对答案不会产生影响我们可以用一个式子来表示 ans[R1+1,L-1]+ans[R+1,L2-1]+1==ans[R1+1,L2-1] （ans[i,j]表示区间[i,j]内能取到的线段总数的最大值）

如果该式子成立就说明它属于我们的答案集合

那么我们现在的问题就变成了如何求ans[i,j]

暴力出奇迹

显然为了保证总体复杂度尽量优秀我们要尽量快的求解

暴力求解显然是不行的

那么该咋办呢？？？？？？？？？？？

当然总有巨佬想出招显然不是我

考虑对于每一条线段选择它以后下一条线段的最优解是确定的

那么我们可以预处理出每一条线段的下一步最优解

但是如果一步一步地慢慢跳显然复杂度是不正确的

想到了啥？？

倍增！

我们可以通过倍增来快速求解

我们用fa[i][j]表示从第i条线段开始往后跳2^j 步后跳到了哪条线段

这样我们就可以愉快地log(n)地求解ans[i,j]了！！！

这题还有一个很关键的地方

我们可以先做一个O（n）预处理处理每个线段的前一个最优线段是啥然后再倒着推回去（于是有了我们的fa 数组）

对于一个线段[l,r]，我们用pre[r]表示在区间[1,r]中，能取到的最多线段数（不包括自己）是由哪个位置转移过来的，然后d[pre[r]]表示是从哪个线段转移过来的。

最开始初始化

FOR(i,1,n) if(pre[r(i)]<l(i)){pre[r(i)]=l(i);id[r(i)]=id(i);}

这样做也可以去掉和自己的r相同但是比自己长的区间（妙啊）

然后是转移

FOR(i,1,tot) if(pre[i]<pre[i-1]){pre[i]=pre[i-1];id[i]=id[i-1];}

然后我们就可以愉快地求出自己是由哪条线段转移过来的啦

FOR(i,1,n) fore[0][id(i)]=id[l(i)-1];

然后整个流程大体就是读入->预处理出线段之间的转移（注意要离散化）->建立倍增数组->贪心求出整体最优解->按字典序逐个枚举并输出答案

整个代码如下：

#include<cstdio>
#include<cctype>
#include<set>
#include<algorithm>
#define Files(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout)
#define End() fclose(stdin);fclose(stdout)
#define ci const int
#define ri register int
#define FOR(i,a,b) for(ri i(a);i<=b;i++)
#define ROF(i,a,b) for(ri i(a);i>=b;i--)
#define l(x) t[x].l
#define r(x) t[x].r
#define id(x) t[x].id
using namespace std;
ci N(200010),logN(21),inf(0x7fffffff);
ci gi(void);
ci log(int x)
{
    if(x<=0) return ~inf;
    ri res(0);while(x>1){res++;x>>=1;}
    return res;
}
struct Interval
{
    int l,r,id;
    bool operator < (const Interval &x)const{return r < x.r || (r == x.r && l <= x.l);}
}t[N];
bool cmp(Interval &x,Interval &y){return x.id < y.id;}
struct El
{
    int id,p;El(){}El(int id,int p){this->id=id;this->p=p;}
    bool operator < (const El &x)const{return p < x.p;}
}t1,t2;

int fore[logN][N<<1];
int pre[N<<1],id[N<<1];
int u[N<<1],tot(0);
int n,logn;
set<El> st;

ci getans(ci &L,int x)
{
    ri ans(0);
    ROF(i,logn,0) if(l(fore[i][x])>L){ans+=(1<<i);x=fore[i][x];}
    return ans;
}
void input()
{
    n=gi();FOR(i,1,n){u[++tot]=l(i)=gi();u[++tot]=r(i)=gi();id(i)=i;}
    sort(u+1,u+tot+1);tot=unique(u+1,u+tot+1)-u-1;
    FOR(i,1,n)
    {
        l(i)=lower_bound(u+1,u+tot+1,l(i))-u;
        r(i)=lower_bound(u+1,u+tot+1,r(i))-u;
    }
    sort(t+1,t+n+1);
    return;
}
void _pre()
{
    logn=log(n)+1;
    FOR(i,1,n) if(pre[r(i)]<l(i)){pre[r(i)]=l(i);id[r(i)]=id(i);}
    FOR(i,1,tot) if(pre[i]<pre[i-1]){pre[i]=pre[i-1];id[i]=id[i-1];}
    FOR(i,1,n) fore[0][id(i)]=id[l(i)-1];
    FOR(j,1,logn) FOR(i,1,n) fore[j][id(i)]=fore[j-1][fore[j-1][id(i)]];
    return;
}
void _getans()
{
    ri tmp(1),ans(0);
    FOR(i,2,n) if(l(tmp)<l(i)) tmp=i;
    tmp=id(tmp);fore[0][n+1]=tmp;
    FOR(i,1,logn) fore[i][n+1]=fore[i-1][fore[i-1][n+1]];
    ROF(i,logn,0) if(fore[i][tmp]){ans+=(1<<i);tmp=fore[i][tmp];}
    printf("%d\n",ans+1);
    return;
}
#undef id
#define p(x) x.p
#define id(x) x.id
void getid()
{
    set<El>::iterator it;
    sort(t+1,t+n+1,cmp);
    st.insert(El(0,0));
    st.insert(El(n+1,inf));
    FOR(i,1,n)
    {
        if(st.lower_bound(El(0,l(i))) != (it = st.lower_bound(El(0,r(i))))) continue;
        t1=*it;t2=*--it;
        if(getans(p(t2),i) + getans(r(i),id(t1)) + 1 != getans(p(t2),id(t1))) continue;
        printf("%d ",i);
        if(i==n) break;
        st.insert(El(i,l(i)));
        st.insert(El(i,r(i)));
    }
    return;
}
int main()
{
    //Files("convention");
    input();
    _pre();
    _getans();
    getid();
    End();
    return 0;
}
#define gc (((p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2))?EOF:*p1++)
char buf[100000],*p1(buf),*p2(buf);
ci gi()
{
    int x(0);bool f(false);char _(gc);
    while(!isdigit(_)){if(_=='-') f=true;_=gc;}
    while( isdigit(_)){x=(x<<3)+(x<<1)+(_^'0');_=gc;}
    return f?-x:x;
}

View Code

注意一下小细节就可以愉快地AC啦~

这么妙的思想当然不是我自己能想出来的文中部分内容引自PhantasmDragon巨佬的题解

感谢 Tom徐提供的(又臭又长的)代码~

感谢阅读~

posted @ 2020-02-26 15:18 HSY2019OIer 阅读(184) 评论(1) 收藏举报

刷新页面返回顶部

HSY2019OIer

【题解】 APIO2009 会议中心

公告