4.21~4.27
CF1013 div3
给个题目链接,就不一题一题截图了:https://codeforces.com/contest/2091
F
比较好的思路:dp+前缀和
用u[i][j]表示从i-1排满足距离条件的点到点(i,j)的所有走法之和,状态转移方程为:
u[i][j] = (prep[i-1][r2] - prep[i-1][l2]);
用p[i][j]表示在第i排满足距离条件的点横着走到点(i,j)的所有走法之和,状态转移方程为:
p[1][j] = (preu[1][r1] - preu[1][l1]);
用preu[i][j]表示第i排的u的前缀和
用prep[i][j]表示第i排的p的前缀和
先特殊处理第1排(起始排),再从2排到n排逐排处理
比较我硬着头皮写的思路和官解的思路,我发现两个本质上差不多,就是实现方法不同
来看看我写的屎:
(dp+BFS)
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int,int>;
const int maxn = 2e3+2;
const int mod = 998244353;
int dp[maxn][maxn],temp[maxn];
char room[maxn][maxn];
int n,m,d, explore[][2] = {0,1,0,-1,1,0,1,-1,1,1};
bool vis[maxn][maxn],vis2[maxn];
inline int dis(int x1,int y1,int x2,int y2){
return ceil(sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)));
}
inline bool check(int x1,int y1,int x2,int y2,int d){
return room[x2][y2] == 'X' && x2>=1 && x2<=n && y2>=1 && y2<=n && dis(x1,y1,x2,y2)<=d;
}
void bfs(int x,int y,int d){
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
vis[i][j] = 0;
vector <int> vec[maxn];
vis[x][y] = 1;
queue <pii> q;
q.push({x,y});
int cnt = 0;
while(!q.empty()){
pii start = q.front();
q.pop();
pii next;
for(int i=0;i<5;i++){
next.first = start.first + explore[i][0];
next.second = start.second + explore[i][1];
if(check(x,y,next.first,next.second,d) && !vis[next.first][next.second] && x!=next.first){
vec[next.first-x].push_back((dp[next.first][next.second])%mod);
cnt = max(cnt,next.first-x);
q.push({next.first,next.second});
vis[next.first][next.second] = 1;
}
}
}
for(int i=0;i<=cnt;i++){
int si = vec[i].size();
sort(vec[i].begin(),vec[i].end(),greater<int>());
//cout << "vec[" << i << "]:\n";
//for(int j=0;j<si;j++){
// cout << vec[i][j] << ' ';
//}
//cout << '\n';
for(int j=0;j<si && j<2;j++){
dp[x][y] = (dp[x][y] + vec[i][j]) % mod;
}
}
//cout << "-------\n";
return;
}
void bfs2(int x,int y,int d){
memset(vis2,0,sizeof(vis2));
vis2[y] = 1;
queue <int> q;
q.push(y);
while(!q.empty()){
int start = q.front();
q.pop();
int next;
for(int i=0;i<2;i++){
next = start + explore[i][1];
if(!vis2[next] && next>=1 && next<=m && room[x][next] == 'X' && dp[x][next] != 0 && abs(next-y)<=d){
q.push(next);
vis2[next] = 1;
temp[y]++;
}
}
}
return;
}
void solve(){
cin >> n >> m >> d;
for(int i=1;i<=n;i++){
memset(temp,0,sizeof(temp));
string s;
cin >> s;
s = ' ' + s;
if(i==n) for(int j=1;j<=m;j++){
room[i][j] = s[j];
dp[i][j] = 1;
}
else for(int j=1;j<=m;j++) room[i][j] = s[j];
}
for(int i=n;i>=1;i--){
bool pd = 1;
for(int j=1;j<=m;j++){
if(room[i][j] == 'X'){
bfs(i,j,d);
pd = 0;
}
}
if(pd){
cout << "0\n";
return;
}
for(int j=1;j<=m;j++){
if(room[i][j]=='X') bfs2(i,j,d);
}
for(int j=1;j<=m;j++)
if(room[i][j]=='X') dp[i][j]+=temp[j];
}
int ans = 0;
for(int j=1;j<=m;j++) ans += dp[1][j];
cout << ans << '\n';
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
dp[i][j] = 0;
solve();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
cout << dp[i][j] << ' ';
cout << '\n';
}
}
return 0;
}
官解是dp+前缀和,看了官解后我重新写了这道题的code,看看官解是多么的优美:
#include <bits/stdc++.h>
#define int long long
#define r1 min(j+d,m)
#define l1 max(j-d-1,0LL)
#define r2 min(j+d-1,m)
#define l2 max(j-d,0LL)
using namespace std;
const int mod = 998244353;
const int maxn = 2e3+2;
int t,n,m,d;
int u[maxn][maxn], p[maxn][maxn], preu[maxn][maxn],prep[maxn][maxn];
char room[maxn][maxn];
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> t;
while(t--){
cin >> n >> m >> d;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin >> room[i][j];
for(int i=0;i<=n;i++)
for(int j=0;j<=m+1;j++)
u[i][j] = p[i][j] = preu[i][j] = prep[i][j] = 0;
for(int j=1;j<=m;j++)
if(room[1][j] == 'X') u[1][j] = 1;
for(int j=1;j<=m;j++)
preu[1][j] = (preu[1][j-1] + u[1][j] +mod)%mod;
for(int j=1;j<=m;j++)
if(room[1][j] == 'X') p[1][j] = (preu[1][r1] - preu[1][l1] + mod)%mod;
for(int j=1;j<=m;j++)
prep[1][j] = (prep[1][j-1] + p[1][j] + mod)%mod;
for(int i=2;i<=n;i++){
for(int j=1;j<=m;j++)
if(room[i][j] == 'X') u[i][j] = (prep[i-1][r2] - prep[i-1][l2] + mod)%mod;
for(int j=1;j<=m;j++)
preu[i][j] = (preu[i][j-1] + u[i][j] + mod)%mod;
for(int j=1;j<=m;j++)
if(room[i][j] == 'X') p[i][j] = (preu[i][r1] - preu[i][l1] + mod)%mod;
for(int j=1;j<=m;j++)
prep[i][j] = (prep[i][j-1] + p[i][j] + mod)%mod;
}
cout << prep[n][m] << '\n';
}
return 0;
}
E
数论。
不必在意如何计算题目里的gcd,lcm,都是障眼法
先欧拉筛筛出2~1e7内的所有素数,再按规律进行处理
找规律的思路如下图所示

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e7+10;
bool vis[N];
vector <int> prime;
int eus(){
int cnt = 0;
for(int i=2;i<=N;i++){
if(!vis[i]) { prime.push_back(i); ++cnt;}
for(int j=0;j<cnt;j++){
if(i*prime[j] > N) break;
vis[i*prime[j]] = 1;
if(i%prime[j] == 0) break;
}
}
return cnt;
}
void solve(int& n,int& si){
ll sum = 0;
for(int i=0;i<si;i++){
if(prime[i] > n) break;
sum += ll(n/prime[i]);
}
cout << sum << '\n';
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int si = eus();
int t;
cin >> t;
while(t--){
int n;
cin >> n;
solve(n,si);
}
return 0;
}
D
贪心。用二分求出最长长凳的最小长度
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,m,k;
cin >> n >> m >> k;
int l=1, r=1e9;
while(l <= r){
int mid = (l+r) >> 1;
if(n*(m - m/mid) >= k) r = mid-1;
else l = mid + 1;
//cout<<"l:"<<l<<" r:"<<r<<'\n';
}
cout << l-1 << '\n';
}
return 0;
}
C
思维题,构造。自己写几组例子,注意到(注意力惊人):
当n为偶数时,不可能构造出来这样的序列;
当n为奇数时,按照1 3 5 ... n 2 4 6.... n-1这样的规律,先输出全部奇数,再输出全部偶数,就是一组构造
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
if(n%2==0){
cout << "-1\n";
continue;
}
for(int i=1;i<=n;i+=2) cout << i << ' ';
for(int i=2;i<n;i+=2) cout << i << ' ';
cout << '\n';
}
return 0;
}
B
贪心,对序列排序。为了让团队数量最多,当a[i] >=x时,就选它一个组成团队;当a[i] < x时,不断往前找,如果找到某a[index],使得a[index]*(i-index+1) < x,ans++。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+1;
int a[maxn];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,x;
cin >> n >> x;
for(int i=0;i<n;i++) cin >> a[i];
sort(a,a+n);
int ans = 0;
for(int i=n-1;i>=0;i--){
if(a[i] >= x) ans++;
else{
//cout << i << ' ';
int index = i;
bool pd = 1;
while(a[index]*(i-index+1) < x){
index--;
if(index < 0){
pd = 0;
break;
}
}
if(pd) ans++;
i = index;
//cout << i << '\n';
}
}
cout << ans << '\n';
}
return 0;
}
A
贪心,开个vector模拟即可
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
vector <int> a = {2,0,2,5,0,3,0,1};
bool pd = 1;
for(int i=1;i<=n;i++){
int cache;
cin >> cache;
vector<int>::iterator it = find(a.begin(),a.end(),cache);
if(it!=a.end()) a.erase(it);
if(pd && a.empty()){
cout << i << '\n';
pd = 0;
}
}
if(pd && !a.empty()) cout << "0\n";
}
return 0;
}
牛客周赛88
E

dp,有点像背包,但不太背包。总的来说不难,但是由于错误使用了memset,这题卡了n久。。。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 2e5+1;
const int inf = -1e16;
int a[maxn],b[maxn],dp[maxn][2];
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,k;
cin >> n >> k;
for(int i=1;i<=n;i++)
cin >> a[i];
for(int i=1;i<=n;i++)
cin >> b[i];
dp[0][1] = dp[0][0] = 0;
dp[1][0] = a[1];dp[1][1] = inf;
for(int i=2;i<=n;i++){
if(dp[i-1][1] >= k && dp[i-1][1]-k+a[i] > dp[i-1][0]+a[i])
dp[i][0] = dp[i-1][1] - k + a[i];
else dp[i][0] = dp[i-1][0] + a[i];
if(dp[i-1][0] >= k && dp[i-1][0]-k+b[i] > dp[i-1][1]+b[i])
dp[i][1] = dp[i-1][0] - k + b[i];
else dp[i][1] = dp[i-1][1] + b[i];
}
cout << max(dp[n][0],dp[n][1]) << '\n';
return 0;
}
D

很简单,直接把x当作二进制,遍历每个数位,遇到0就能构造出y,没有0就输出-1
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int x;
cin >> x;
int x1 = x, times = 0;
while(1){
//cout << x1 << '\n';
if(x1 == 0){
cout << "-1\n";
break;
}
if(!(x1 & 1)){
cout << pow(2,times) << '\n';
break;
}
x1 = x1 >> 1;
times++;
}
}
return 0;
}
C

和B差不多,C题是只要某个点的x or y坐标和它所对的中点的x or y坐标相等即可
#include <bits/stdc++.h>
using namespace std;
double x[4], y[4], x_z[4], y_z[4];
void pd(){
for(int i=1;i<=3;i++){
if(x[i] == x_z[i]){
cout << "YES\n";
return;
}
}
for(int i=1;i<=3;i++){
if(y[i] == y_z[i]){
cout << "YES\n";
return;
}
}
cout << "NO\n";
return;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
for(int i=1;i<=3;i++)
cin >> x[i] >> y[i];
x_z[1] = (x[2] + x[3])/2.0;
x_z[2] = (x[1] + x[3])/2.0;
x_z[3] = (x[1] + x[2])/2.0;
y_z[1] = (y[2] + y[3])/2.0;
y_z[2] = (y[1] + y[3])/2.0;
y_z[3] = (y[1] + y[2])/2.0;
//for(int i=1;i<=3;i++) cout << x[i] << ' ' << y[i] << '\n';
pd();
}
return 0;
}
B

很简单的题,只需要判断三角形三个顶点与三个中点,是否存在某个顶点的x or y坐标和某个中点x or y坐标同时为0即可
#include <bits/stdc++.h>
using namespace std;
double x[4], y[4], x_z[4], y_z[4];
void pd(){
for(int i=1;i<=3;i++){
if(x[i] == 0)
for(int j=1;j<=3;j++)
if(x_z[j] == 0){
cout << "YES\n";
return;
}
if(y[i] == 0)
for(int j=1;j<=3;j++)
if(y_z[j] == 0){
cout << "YES\n";
return;
}
}
cout << "NO\n";
return;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
for(int i=1;i<=3;i++)
cin >> x[i] >> y[i];
x_z[1] = (x[1] + x[2])/2.0;
x_z[2] = (x[2] + x[3])/2.0;
x_z[3] = (x[1] + x[3])/2.0;
y_z[1] = (y[1] + y[2])/2.0;
y_z[2] = (y[2] + y[3])/2.0;
y_z[3] = (y[1] + y[3])/2.0;
//for(int i=1;i<=3;i++) cout << x[i] << ' ' << y[i] << '\n';
pd();
}
return 0;
}
A

签到题,略过
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int a,b,c;
cin >> a >> b >> c;
if(a*b <= c) cout << "YES\n";
else cout << "NO\n";
return 0;
}
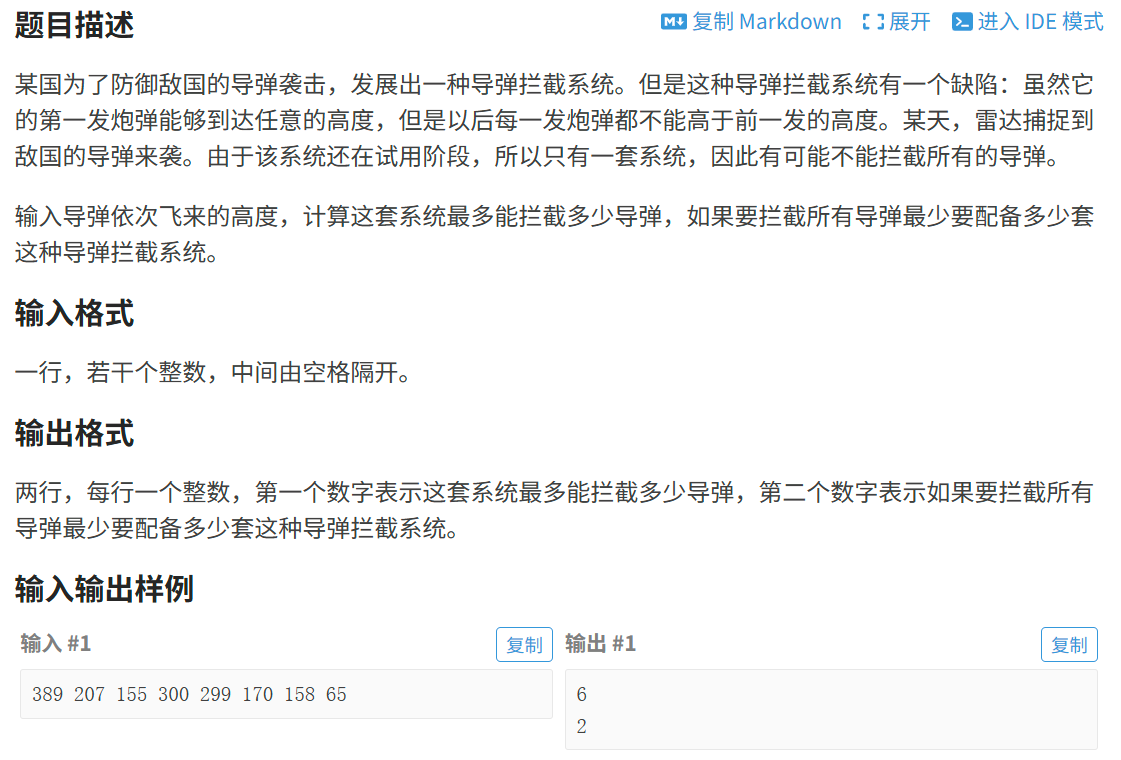
改版经典--导弹拦截
这道题二十多年了,比我都大......
这道最长不上升子序列 我去年做过最原始的版本,原始解法是dp,复杂度O(n2),今天重新写了dp的code,很简短简单:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int a[maxn], dp[maxn];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int cnt = 0, ans = 0, sum = 1;
while(cin >> a[++cnt]);cnt--;
for(int i=1;i<=cnt;i++) dp[i] = 1;dp[0]=0;
for(int i=1;i<=cnt;i++){
for(int j=i+1;j<=cnt;j++){
if(a[j] <= a[i]){
dp[j] = max(dp[j],dp[i]+1);
ans = max(ans,dp[j]);
}
}
}
cout << ans << '\n';
return 0;
}
来看洛谷P1020
题还是那道题,但是数据加强了,老套的n2的dp过不了这道题
因此用O(nlogn)的二分来做
二分可以用C++标准模板库里的lower_bound()和upper_bound()来实现
但要注意:二分只能实现找到最长上升/非降子序列(Lis/Lnds)的长度,但是子序列的内容不一定正确!
找最长上升子序列的二分方法:
一个队列(推荐用vector),从小到大排队,
下一个数如果**>**队尾元素,那么就排到队尾。
下一个数如果**<=**队尾元素,那么就找到队内的第一个**>=**该元素的值,然后替换它
vector <int> vec;
vec.push_back(a[0]);
for(int i=1;i<=n;i++){
if(a[i] > *vec.rbegin()) vec.push_back(a[i]);
else *lower_bound(vec.begin(),vec.end(),a[i]) = a[i];
}
找最长非降子序列的二分方法:
一个队列(推荐用vector),从小到大排队,
下一个数如果**>=**队尾元素,那么就排到队尾。
下一个数如果**<**队尾元素,那么就找到队内的第一个**>**该元素的值,然后替换它
vector <int> vec;
vec.push_back(a[0]);
for(int i=1;i<=n;i++){
if(a[i] >= *vec.rbegin()) vec.push_back(a[i]);
else *upper_bound(vec.begin(),vec.end(),a[i]) = a[i];
}
本道题的二分code:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int a[maxn];
vector <int> lnis/*最长不升子序列*/, lis/*最长上升子序列*/;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n = 0;
while(cin >> a[n++]);n--;
lnis.push_back(a[0]);
lis.push_back(a[0]);
for(int i=1;i<n;i++){
if(a[i] <= *lnis.rbegin()) lnis.push_back(a[i]);
else *upper_bound(lnis.begin(),lnis.end(),a[i],greater<int>()) = a[i];
if(a[i] > *lis.rbegin()) lis.push_back(a[i]);
else *lower_bound(lis.begin(),lis.end(),a[i]) = a[i];
}
cout << lnis.size() << '\n' << lis.size() << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号