2.3~2.9
牛客寒假训练营1
大家都报了训练营呐,那我也报一个 v(虽晚不亏)
补一下之前的
A
题目
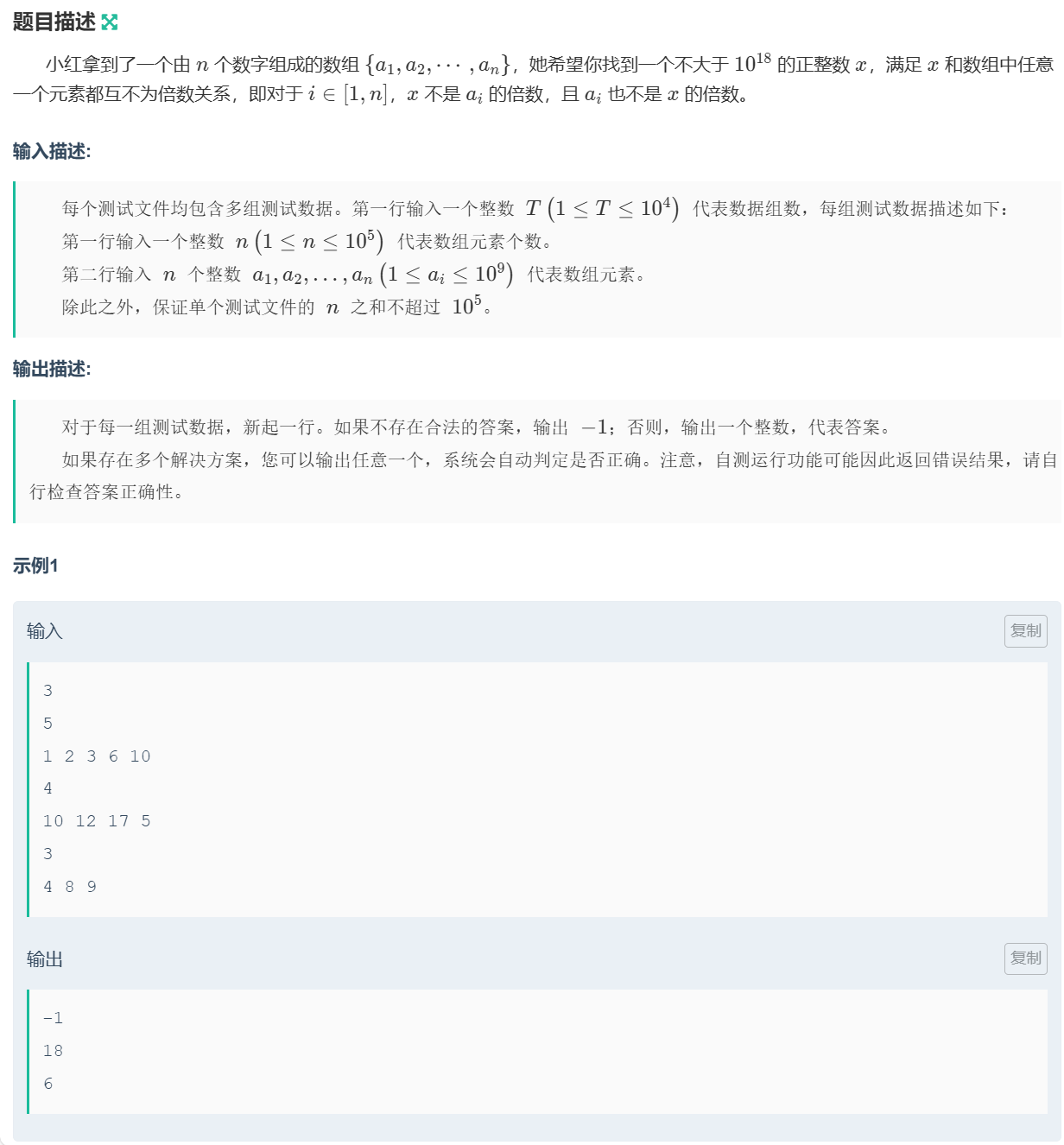
这题考察素数。由题目得,ai不超过1e9,因此如果给的数有1就输入-1(1和任何数都构成倍数关系),否则输出任意一个比1e9大的素数、
那比1e9大的素数怎么找呢?
新开一个cpp,用埃氏筛把这个数找到,是999999937,CV
代码
埃氏筛
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e9+5;
bool visi[maxn];
vector <int> prime;
void sushu(){
for(int i=2;i*i<maxn;i++)
if(!visi[i])
for(int j=i*i;j<maxn;j+=i)
visi[j] = true;
for(int i=2;i<maxn;i++)
if(!visi[i]) prime.push_back(i);
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
sushu();
cout << *prime.rbegin();
return 0;
}
题目代码
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,cache,pd=0;
cin >> n;
for(int i=0;i<n;i++){
cin >> cache;
if(cache == 1) pd=1;
}
cout << (pd==1 ? "-1\n" : "999999937\n");
}
return 0;
}
B
题目
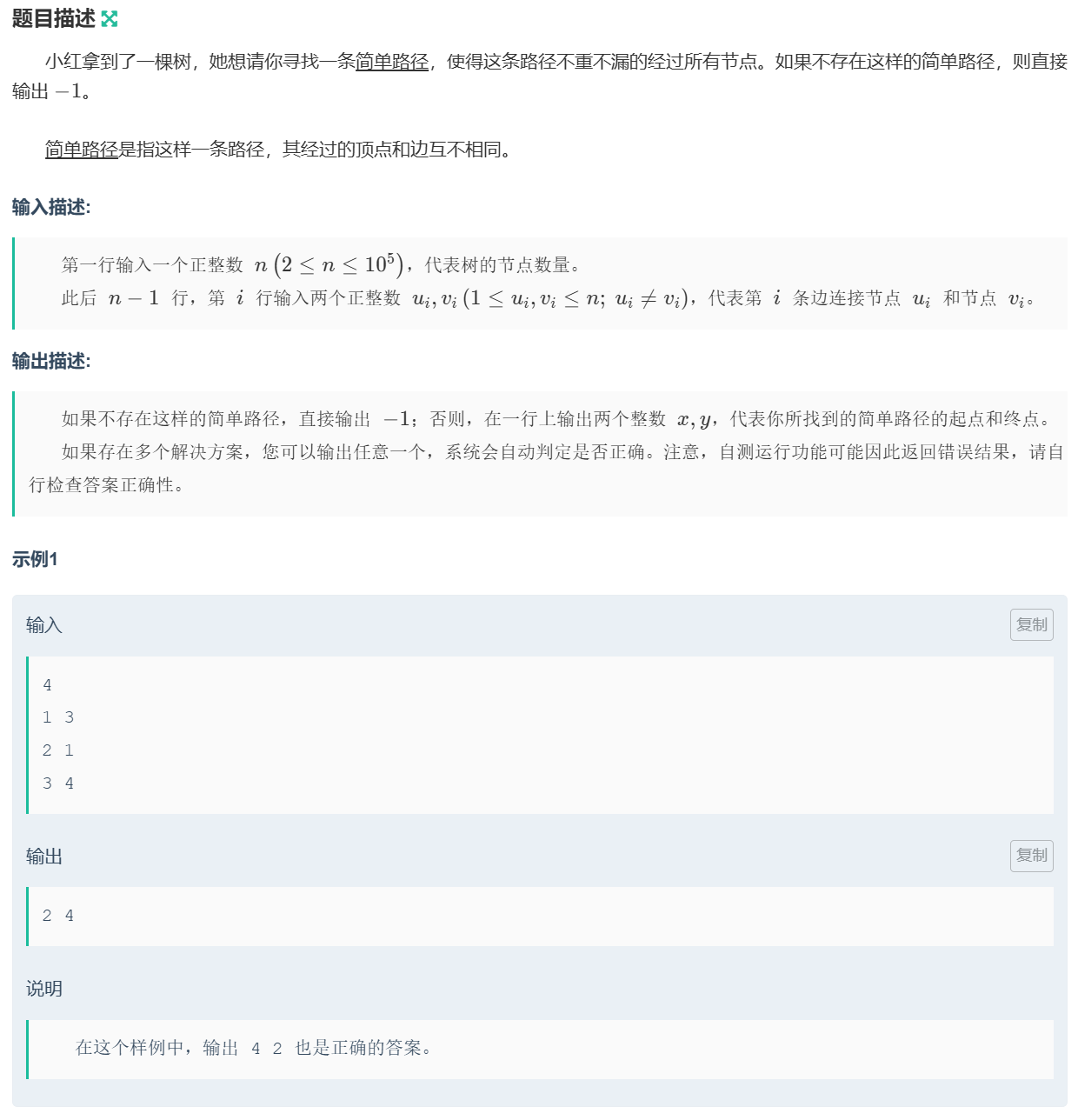
有2个度数为1的点就满足单条路径,其他情况都不满足。因此记录每个顶点出现的次数,然后逐一判断即可
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,hash[maxn]={0},sum=0;
vector <int> oup;
cin >> n;
n--;
while(n--){
int cache;
cin >> cache;
hash[cache]++;
cin >> cache;
hash[cache]++;
}
for(int i=1;i<maxn;i++)
if(hash[i] == 1) oup.push_back(i);
if(oup.size()==2) cout << oup[0] << ' ' << oup[1] << '\n';
else cout << "-1\n";
return 0;
}
D
题目
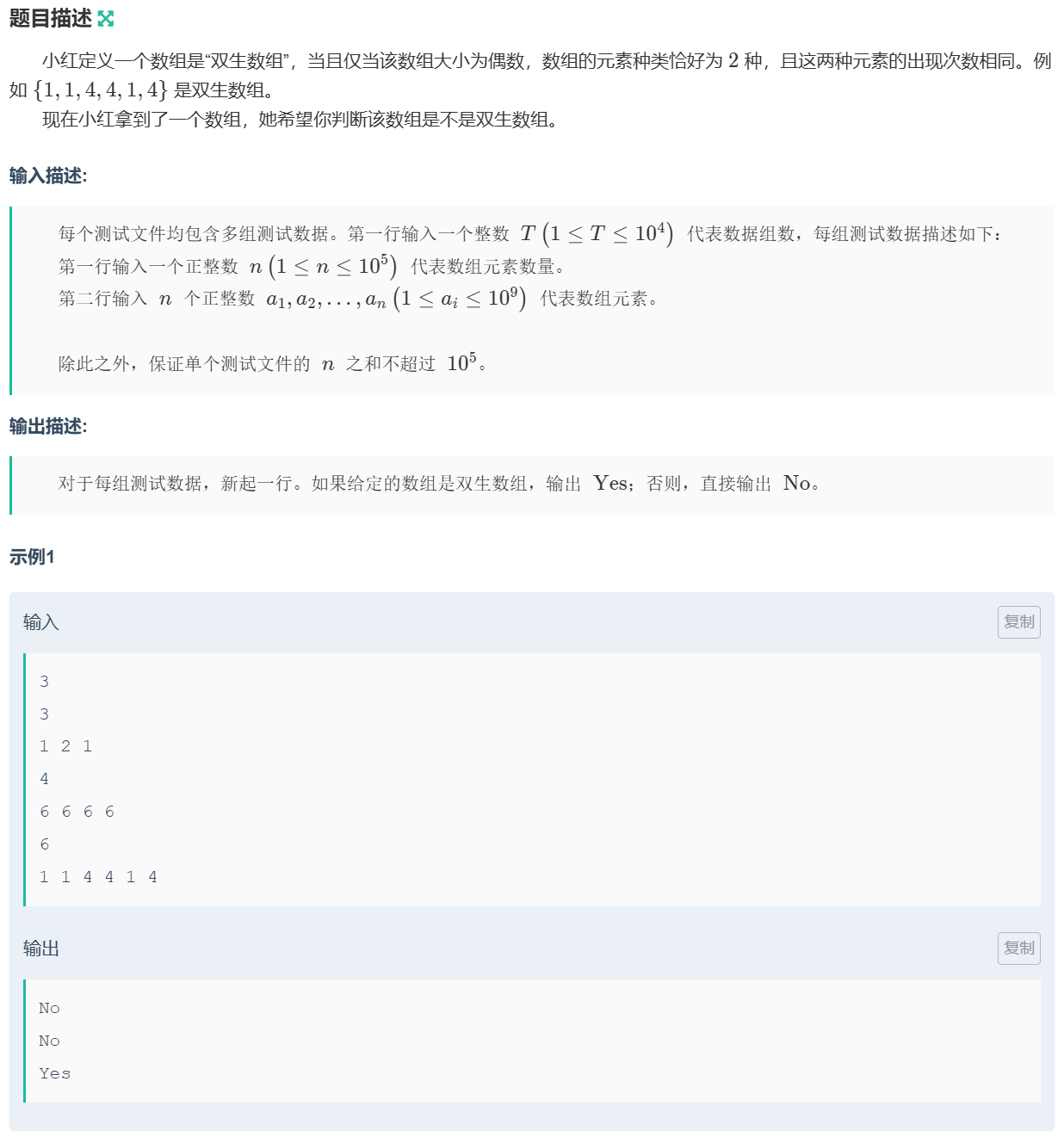
这道题利用map的特性就行,size不是二或者可key1和key2对应的value不一样就是No,否则Yes
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
map <int,int> m;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,cache;
cin >> n;
for(int i=0;i<n;i++){
cin >> cache;
m[cache]++;
}
if(m.size()!=2) cout << "No\n";
else{
int i1;
map<int,int>::iterator it=m.begin();
i1 = it->second;
//cout << "i1:"<<i1 << '\n';
it++;
if(i1 == it->second) cout << "Yes\n";
else cout << "No\n";
}
m.clear();
}
return 0;
}
G
题目

显然,如果能够实现的话,1~n的和一定等于数组的和
接着对输入的数组进行排序,再从1~n和数组逐一相减,由于两者和相等,因此相减之和为0,我们只需要取其中正数和即可,正数和就是最小操作次数
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,cache,sum=0;
vector <int> arr;
void solve(){
int shang=0;
if((1+n)*n != sum*2){
cout << -1;
return;
}
sort(arr.begin(),arr.end());
for(int i=1;i<=n;i++){
if(arr[i-1] < i)
shang += i-arr[i-1];
}
cout << shang;
return;
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i=0;i<n;i++){
cin >> cache;
arr.push_back(cache);
sum+=cache;
}
solve();
return 0;
}
E
题目

涉及知识盲区了qwq,中位数定理:
要将一个有序数组通过+1或-1的n次操作变换为全部相等数所需的操作次数,就是每个数变换为中位数的操作次数之和
将给的数组排序吗,然后分为前后两部分操作。需要注意的是如果前后中位数相等,那么就要分为前中位数--和后中位数++这两种情况来讨论,取其中较小次数的情况
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e5;
vector <int> arr;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,cache,times=0,front,back;
cin >> n;
int half = n/2;
for(int i=0;i<n;i++){
cin >> cache;
arr.push_back(cache);
}
sort(arr.begin(),arr.end());
if(half%2==0){
front = (arr[half/2-1]+arr[half/2])/2;
back = (arr[half+half/2-1]+arr[half+half/2])/2;
}
else{
front = arr[half/2];
back = arr[half+half/2];
}
if(front != back){
for(int i=0;i<half;i++)
times += abs(front-arr[i]);
for(int i=half;i<n;i++)
times += abs(back-arr[i]);
cout << times << '\n';
}
else{
int times1=0,times2=0;
front--;
for(int i=0;i<half;i++)
times1 += abs(front-arr[i]);
for(int i=half;i<n;i++)
times1 += abs(back-arr[i]);
front++,back++;
for(int i=0;i<half;i++)
times2 += abs(front-arr[i]);
for(int i=half;i<n;i++)
times2 += abs(back-arr[i]);
cout << (times1<times2 ? times1:times2) << '\n';
}
arr.clear();
}
return 0;
}
M
题目

最小化极差只能贪心来求,因为想要极差最小,只能让最小数尽可能小。而每次进行*2操作后,最大值和最小值可能出现这些变化:
- 最小值*2还是数组最小值
- 最小值*2大于原来的最大值
- 最小值*2比现在的最小值大,比现在的最大值小
考虑维护最小区间端点 l r,若次小值不在最小区间内,那么就把最小区间延伸到次小值处,延伸区间的每个数都要*2,延伸完后更新极差。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int man = 1e5+1;
pair <int,int> arr_1[man];
int arr_2[man];
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,maxn,minn,jicha;
cin >> n;
for(int i=0;i<n;i++){
cin >> arr_1[i].first;
arr_1[i].second = i;
arr_2[i] = arr_1[i].first;
}
arr_1[n].first = 1e10;
sort (arr_1,arr_1+n);
maxn = max(arr_1[n-1].first,arr_1[0].first*2);
minn = min(arr_1[0].first*2,arr_1[1].first);
jicha = maxn - minn;
int l = arr_1[0].second, r = arr_1[0].second;
for(int i=1;i<n;i++){
while(arr_1[i].second<l){
l--;
maxn = max(maxn,arr_2[l]*2);
minn = min(arr_1[0].first*2,arr_1[i+1].first);
}
while(arr_1[i].second>r){
r++;
maxn = max(maxn,arr_2[r]*2);
minn = min(arr_1[0].first*2,arr_1[i+1].first);
}
minn = min(arr_1[0].first*2,arr_1[i+1].first);
jicha = min(jicha,maxn-minn);
}
cout << jicha << '\n';
return 0;
}
牛客寒假训练营4
K
题目
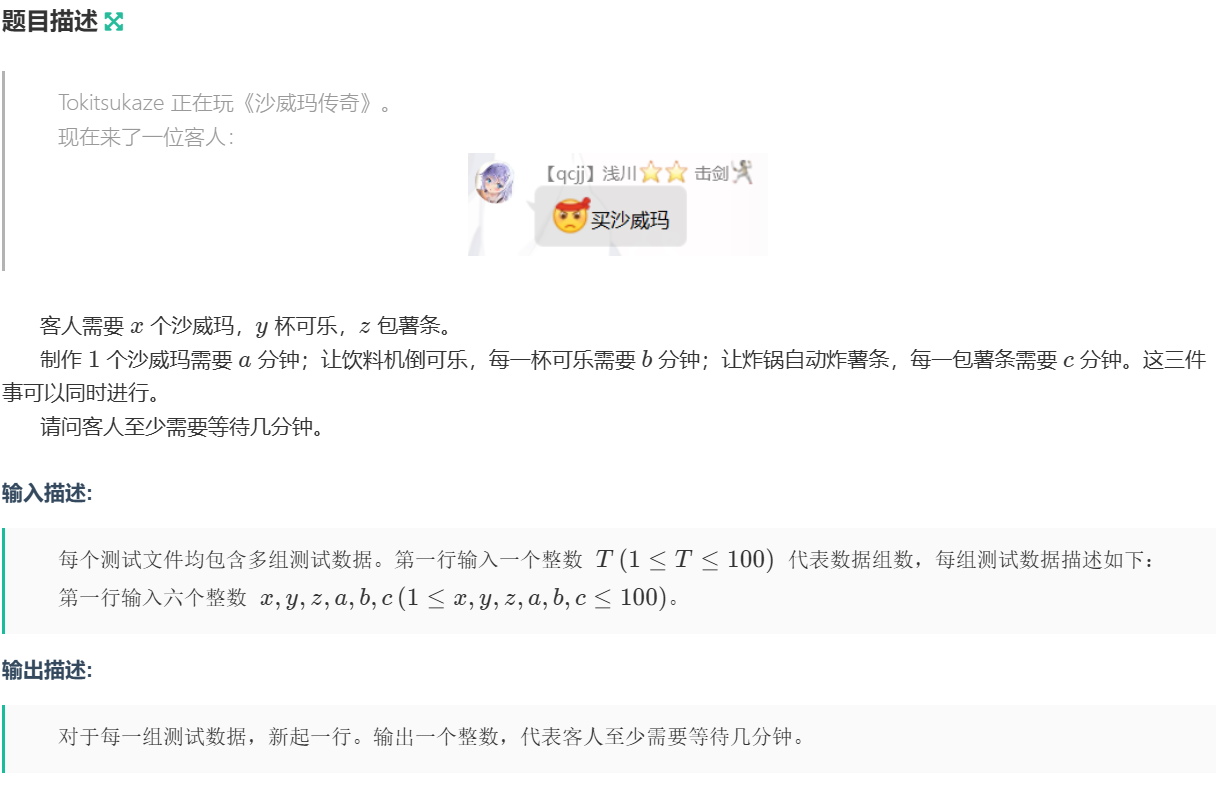
签到,输出xa,yb,z*c里最大的
代码
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int x,y,z,a,b,c;
cin >> x >> y >> z >> a >> b >> c;
cout << max(x*a,max(y*b,z*c)) << '\n';
}
return 0;
}
I
题目
思路:先做一个字符u数量的前缀和,然后进行字符串uwawauwa的匹配,匹配上的就加上第 i-2 个前缀和
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+1;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
string muban = "uwawauwa";
while(t--){
int n,qz[maxn]={0},sum=0;
cin >> n;
string s;
cin >> s;
if(n<10){
cout << "0\n";
continue;
}
if(s[0]=='u') qz[0]=1;
for(int i=1;i<n;i++)
qz[i] = qz[i-1] + (s[i] == 'u');
for(int i=n-8;i>0;i--){
int pd=1;
for(int j=0;j<8;j++)
if(s[i+j] != muban[j]){
pd=0;
break;
}
if(pd) sum+=qz[i-2];
}
cout << sum << '\n';
//for(int i=0;i<n;i++) cout << qz[i] << ' ';
}
return 0;
}
E
题目

龙之吐息是往斜线蔓延的,相当于求每条斜线的和。我们知道,正斜线 \ 上每个格子的行数与列数之差是固定的,反斜线 / 上每个格子的行数与列数之和是固定的。做一个每条正反斜线的和,然后每个格子 =
sum1[i+j]+sum2[i-j+1000]-room[i][j]
其中1000是为了保证i-j+1000是个正数。
赛时用3个不同的方法写这道题,相当于做了3道题,都TLE......
最后在第三个方法的基础上做了一些优化,删了一些不必要的代码就过了
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int room[1002][1002],n,m;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int maxn=0,sum1[2002]={0},sum2[3002]={0};
cin >> n >> m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cin >> room[i][j];
sum1[i+j] += room[i][j];
sum2[i-j+1000] += room[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int temp = sum1[i+j]+sum2[i-j+1000]-room[i][j];
if(temp > maxn) maxn = temp;
}
cout << maxn << '\n';
}
return 0;
}
B
题目

用dfs搜,碰到"?"就分支,然后每条枝上对每个0或1反转操作后进行判断,如果01和10数量相等就是平衡的
赛后看题解,天塌了,不肖这么麻烦,整串的第一个和最后一个字符相等就一定平衡,好神奇的规律...
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9 + 7;
void dfs(int pos,string& temp,const string& s, int& sum_val){
if(pos == s.size()){
int n = temp.size(), val = 0;
for(int i=0;i<n;i++){
string t = temp;
t[i] = (t[i] == '0') ? '1' : '0';
int sum01=0, sum10=0;
for(int j=0;j<n-1;j++){
char a = t[j], b = t[j+1];
if(a == '0' && b == '1')
sum01++;
else if(a == '1' && b == '0')
sum10++;
}
if(sum01 == sum10)
val++;
}
sum_val += val;
return;
}
if(s[pos] == '?'){
temp.push_back('0');
dfs(pos+1,temp,s,sum_val);
temp.pop_back();
temp.push_back('1');
dfs(pos+1,temp,s,sum_val);
temp.pop_back();
}else{
temp.push_back(s[pos]);
dfs(pos+1,temp,s,sum_val);
temp.pop_back();
}
}
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n;
string s;
cin >> n >> s;
int sum_val = 0;
string temp;
dfs(0,temp,s,sum_val);
cout << sum_val % MOD << '\n';
}
return 0;
}
C
题目

赛时没有发现,这道题有个结论:
- 字符串首尾相等必定平衡
- 字符串首尾不等必定不平衡
因此,对于首尾平衡的,中间就有2^(n-2)种情况;首尾不平衡,反置一个就平衡
?的情况进行分类讨论
注意特判:如果n=1,始终平衡;这时如果有?,就是2,否则为1
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e9+7;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,num=0;
cin >> n;
string s;
cin >> s;
if(n==1){
cout << (s[0]=='?' ? "2\n":"1\n");
continue;
}
int k1=1,k2=1,sum=0;
for(int i=0;i<=n;i++) if(s[i]=='?') num++;
for(int i=1;i<=num;i++){
k1 *= 2;
k1 %= maxn;
}
for(int i=1;i<=num-1;i++){
k2 *= 2;
k2 %= maxn;
}
if(s[0] != '?' && s[n-1] != '?'){
if(s[0]==s[n-1]) sum = k1*(n-2)%maxn;
else sum = k1*2%maxn;
}
else sum = k2*n%maxn;
cout << sum << '\n';
}
return 0;
}
D
题目

消除,用短串的不同字符消除长串,如果该字符短串有而长串没有,就无法消除,sum++;消除完后,长串会有剩余字符,其中一些字符可能可以两两相消,如果最后字母个数为奇数就会剩一个消不了,ans++;
如果sum>ans,就是sum
否则是sum+[(ans-sum)/2]
代码
#include <bits/stdc++.h>
using namespace std;
map <char,int> ma;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,m;
string a,b;
cin >> n >> m;
cin >> a >> b;
if(n<m){
swap(n,m);
swap(a,b);
}
for(int i=0;i<n;i++)
ma[a[i]]++;
int ans=0,sum=0;
for(int j=0;j<m;j++){
if(ma[b[j]]) ma[b[j]]--;
else sum++;
}
for(auto i:ma)
if(i.second%2 == 1) ans++;
if(sum >= ans) ans = sum;
else{
ans -=sum;
ans /=2;
ans +=sum;
}
cout << ans <<'\n';
ma.clear();
}
return 0;
}
牛客周赛79
A
题目

签到
代码
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int x;
cin >> x;
if(x==1) cout << -1;
else cout << 2*x;
return 0;
}
B
题目

数学题,贪心。
对于最大值,连着选肯定最大,n/2
对于最小值,隔一个选肯定最小,n/3;注意,如果还剩下两个就要+1,因此为
n/3 + (n%3==2 ? 1:0)
代码
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
cout << n/3+(n%3==2 ? 1:0) << ' ' << n/2;
return 0;
}
C
题目

由于满二叉树的特殊性(每个节点,如果不是叶子节点,则都有两个子节点),可以观察规律,用公式做:
如果该节点有儿子,那么左二 -> 右儿有1条路
如果该节点有孙子,到孙子就有4条路
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9+7;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
cin >> n;
int sum=0,m=1;
while(n){
if(n>=3)
sum = (sum+m*5)%mod;
else if(n==2) sum = (sum+m)%mod;
m = m*2%mod;
n--;
}
cout << sum << '\n';
return 0;
}
D
题目

x的位数太高,转化为字符串做。面对如此大的位数,为了尽可能简化,尽量只在前几位输出一个素数,后面都是0
考虑x的首位,
为1,则输出2和n-1个0;
为2,则输出3和n-1个0......以此类推
当大于等于6时,就输出11即可,后面也是n-1个0
代码
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
string s;
cin >> s;
int wei = s.size();
if(s[0] == '1')
cout << '2';
else if(s[0] == '2')
cout << '3';
else if(s[0] == '3' || s[0] == '4')
cout << '5';
else if(s[0] == '5')
cout << '7';
else if(s[0] == '6' || s[0] == '7' || s[0] == '8' || s[0] == '9')
cout << "11";
for(int i=1;i<wei;i++) cout << '0';
cout << '\n';
}
return 0;
}
牛客寒假训练营5
A
题目

找特殊的数据
+:1和x-1
-: x+1和1
*:1和x
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int x;
char fu;
cin >> x >> fu;
if(fu == '+'){
cout << 1 << ' ' << x-1 << '\n';
}
else if(fu == '-'){
cout << x+1 << ' ' << "1\n";
}
else{
cout << 1 << ' ' << x << '\n';
}
return 0;
}
J
题目

模拟题(梦回高中物理)
每秒钟分别对油门、刹车、离合三种情况处理速度的变化,再算该秒内驶过的路程即可
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
string s;
signed main (void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,v=0,sum=0;
cin >> n >> s;
for(int i=0;i<n;i++){
int lihe=0,v1;
if(s[i] == '0') v+=10;
else if(s[i] == '1') v = (v-5>=0 ? v-5:0);
else{
v1 = v;
v = (v-10>=0 ? v-10:0);
lihe=1;
}
sum += v;
if(lihe) v = v1;
}
cout << sum;
return 0;
}
B
题目

"隔板法"
有k个隔板,每个隔板的前面都放t个东西,剩余的东西放在最后一个隔板的后面
这是这道题的主要思路,有特判,当t+k > n 时,形成不了鸡场,为0
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int T;
cin >> T;
while(T--){
int n,t,k,ans=0;
cin >> n >> t >> k;
if(t+k > n) cout << "0\n";
else{
int res = n-k;
int zu = res/t;
if(zu>=k+1) cout << k+1 << '\n';
else cout << zu << '\n';
}
}
return 0;
}
I
题目

由瞪眼法,只要m和n都不为0,那么它们必定可以化到对方去
当m和n都为0时,0=0,也成立 (坑点!)
当m和n其中一个为0时,必定不成立
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
while(t--){
int n,m;
cin >> n >> m;
if(n==0 && m==0) cout << "Yes\n";
else if(n==0 || m==0) cout << "No\n";
else cout << "Yes\n";
}
return 0;
}
Algorithm--算法学习
滚动数组--dp空间优化
dp状态方程常常是二维以上的,占用空间多。从状态方程
dp[i][j] = max(dp[i-1][j-c[i]]+w[i],dp[i-1][j])可以看出,dp[i][]只与dp[i-1][]有关,所以就用新的一行覆盖已经无用的一行(滚动),只需要两行就够了。
for(int i=1; i<=n; i++}
for(int j=C; j>=c[i]; j--)
dp[j] = max( dp[j], dp[j-c[i]] + w[i] );
要注意:j 应该反过来循环,即从后向前覆盖,否则同一个物品可能会被装两次
优化后DP的空间复杂度从O(N×C)降低到O(C)
话不多说,来一道题
题目
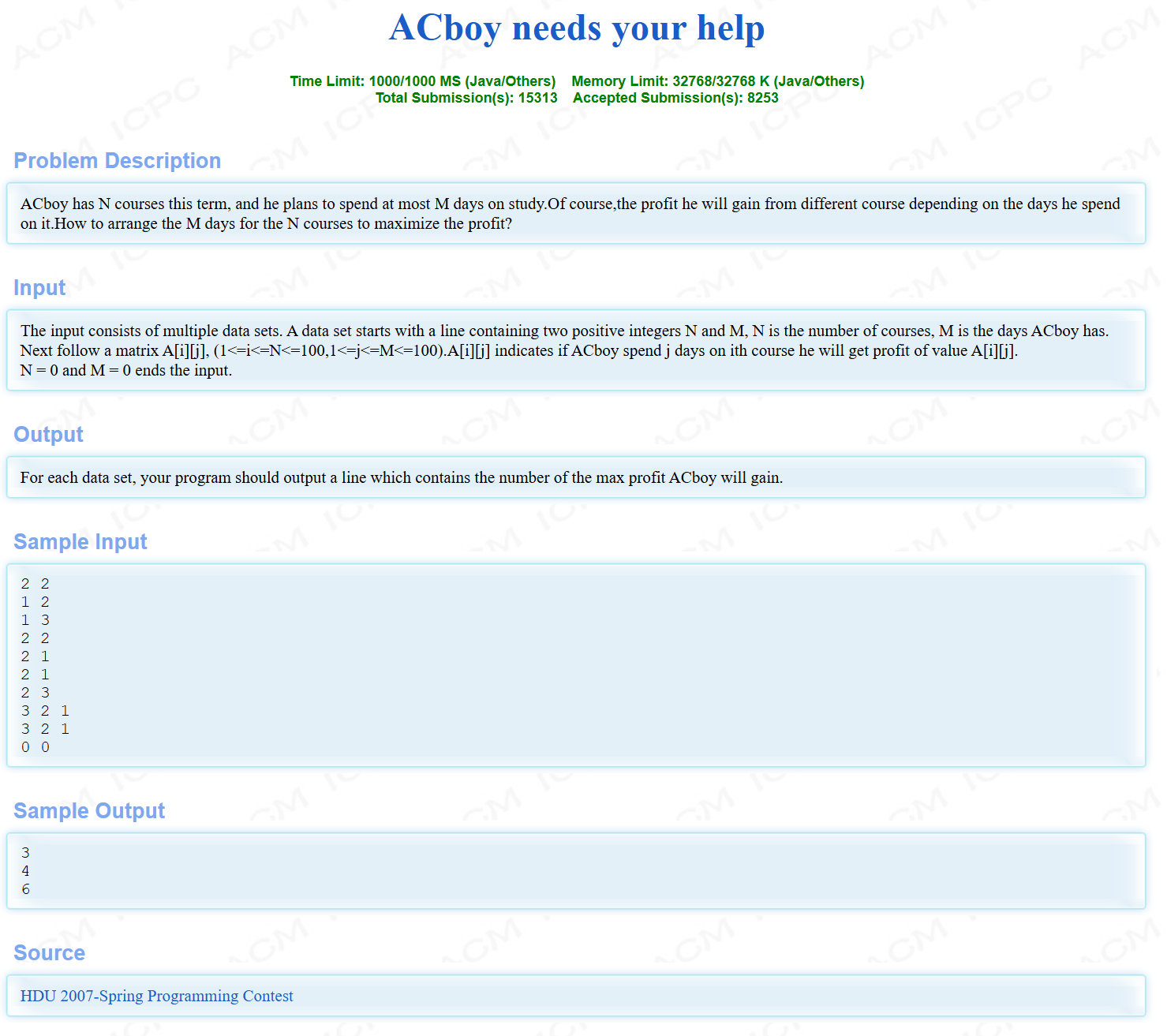
这道题是分组背包,需要三层循环
代码
#include <bits/stdc++.h>
using namespace std;
int dp[101],c[101][101];
void read(int N,int M){
memset(c,0,sizeof(c));
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
cin >> c[i][j];
}
int solve(int N,int M){
memset(dp,0,sizeof(dp));
for(int i=1;i<=N;i++)
for(int j=M;j>=0;j--) //j要反向
for(int k=1;k<=M;k++)
if(j>=k)
dp[j]=max(dp[j],dp[j-k]+c[i][k]); //滚动数组
return dp[M];
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int N,M;
cin >> N >> M;
while(N || M){
read(N,M);
cout << solve(N,M) << '\n';
cin >> N >> M;
}
return 0;
}
差分
差分是前缀和的逆运算,运用于区间修改和询问。当对数据集A的某个区间做修改时,引入差分数组D,只需要修改这个区间的端点,就能记录整个区间的修改,这个修改的复杂度为O(1) 。当所有修改都完成后,再利用差分数组计算出新的A。
差分数组D[]的定义是:D[k] = a[k] - a[k-1],a[]是原数组
显然,a[i] = D[1]+D[2]+...+D[i],a[]是D[]的前缀和
例如,把数组区间[L,R]内的每个元素都加上d,只需要对应的差分数组D[]做以下操作:
把D[L]加上d:D[L] += d;
把D[R+1]减去d:D[R+1] -= d;
D[]只会修改区间[L,R]内的只,不会修改到区间外的,要查询a[i]时,做一个D[i]的前缀和即可
以HDU 1556 为例
题目
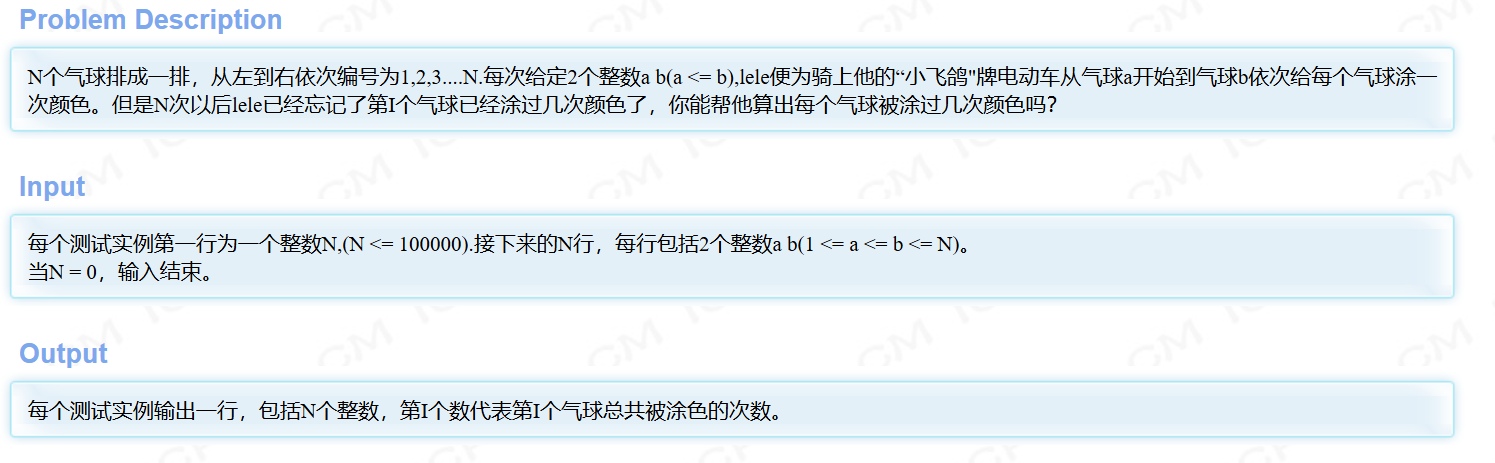
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+1;
int a[maxn],D[maxn];
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n;
while(cin >> n){
int l,r;
memset(a,0,sizeof(a));
memset(D,0,sizeof(D));
for(int i=1;i<=n;i++){
cin >> l >> r;
D[l]++;D[r+1]--;
}
for(int i=1;i<=n;i++){
a[i] = a[i-1] + D[i];
cout << a[i] << ' ';
}
cout << '\n';
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号