【讲解】KMP

首先引入一个问题，给出两个字符串 \(A\) 和 \(B\) （字符串以 \(1\) 为下标开头），长度分别为 \(n\) 和 \(m\) ，若 \(A\) 的区间 \([l,r](1\le l \le r \le n)\) 与 \(B\) 完全相同，则称 \(B\) 在 \(A\) 中出现，问满足条件的区间的位置

很容易想到暴力算法，枚举 \(l\) ，然后判断是否相等，时间复杂度为 \(O(nm)\)

这时候便需要 KMP 了，它分为两步

1. 对字符串 \(B\) 自我匹配，求出数组 \(next\) ， 其中 \(next[i]\) 表示 \(B\) 中以 \(i\) 结尾的非前缀子串与 \(B\) 的前缀能够匹配的最长长度（位置）

2. 对字符串 \(B\) 与 \(A\) 进行匹配，枚举每一个 \(i(1\le i\le n)\) ，表示 \(A\) 中以 \(i\) 结尾的子串与 \(B\) 的前缀能够匹配的最长长度（位置）

只要在第二步中，最长长度刚好为 \(m\) ，那么这便是 \(B\) 出现的位置

下面来讨论 \(next\) 的计算方法

首先我们知道， \(next[1]=0\) （匹配失败，一个数字都没有匹配个啥），那么就可以通过这个来递推求解整个 \(next\) 数组

为了叙述方便，我们称满足 \(j<i\) 且 \(B[i-j+1,i]=B[1,j]\) 的 \(j\) 为 \(next[i]\) 的候选项

举个例子：让字符串 \(B\) 为 \(abababaac\) ， \(i\) 为 \(7\) ，那么 \(next[i]=5\) ，而 \(next[i]\) 的候选项为 \(5，3，1\)

这里就有一个很显然的结论 \(next[i]\) 为 \(next[i]\) 的最大候选项

在正式计算 \(next\) 数组前，先来一个引理

---

引理：若 \(j_0\) 为 \(next[i]\) 的候选项，那么有两个结论必定成立——

1. \([next[j_0]+1,j_0-1]\) 之间的数均不是 \(next[i]\) 的候选项

2. \(next[j_0]\) 必定为 \(next[i]\) 的候选项

3. 若 \(j_0\) 为 \(next[i]\) 的候选项，则 \(j_0-1\) 为 \(next[i-1]\) 的候选项

证明：

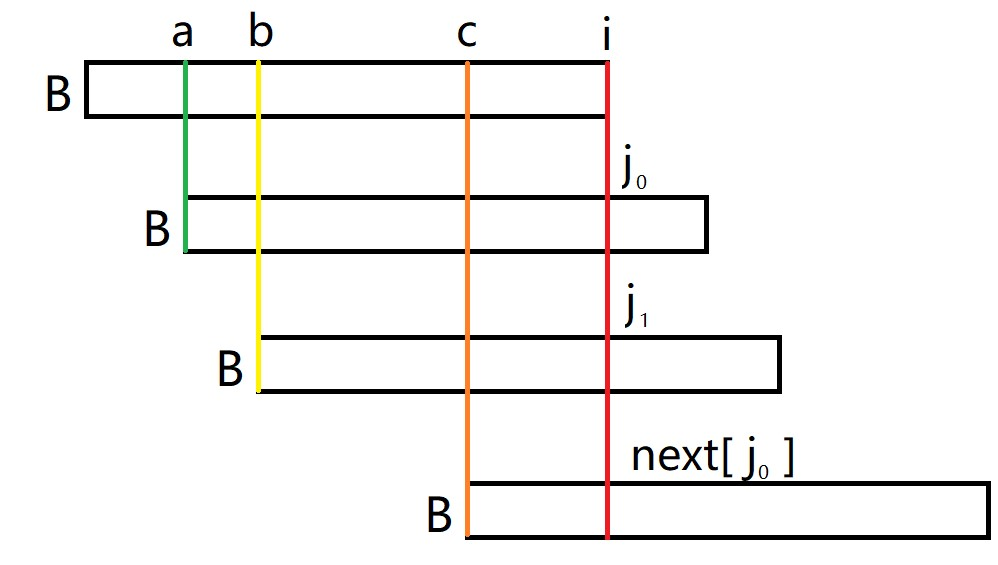
假设存在 \(next[j_0]<j_1<j_0\) ，且 \(j_1\) 为 \(next[i]\) 的候选项，那么可以得到这一张图

注意：

• 图中的 \(a,b,c\) 均可以用仅含 \(i,j_0,j_1,next[j_0]\) 的式子表达，这里只是为了表述方便使用字母

• 任意两条有颜色的线之间都相等

根据这张图可以看出，若 \(j_0\) 为 \(next[i]\) 的候选项，那么 \(next[j_0]\) 必定为 \(next[i]\) 的候选项

这是显然的， \(B[1,next[j_0]]=B[c,j_0]\)，而 \(B[1,j_0]=[a,i]\) 的前提是 \(B[c,j_0]=B[c,i]\) ，也就是说 \(B[1,next[j_0]]=B[c,i]\) ，这不就是候选项的定义吗，所以 \(next[j_0]\) 为 \(next[i]\) 的候选项，这样第二个结论得证

在第一个结论中，因为 \(B[1,j_0]=B[a,i]\) ，所以 \(B[b,j_0]=B[b,i]\)

又因为 \(B[1,j_1]=B[b,i]\) ，则有 \(B[1,j_1]=B[b,j_0]\) ，也就是说 \(j_1\) 也是 \(next[j_0]\) 的候选项，这与 \(next[j_0]\) 是 \(next[j_0]\) 的最大候选项矛盾，得证

第三个结论证法类似（而且挺明显的），不再赘述

---

根据引理 \(1\) 和引理 \(2\) ，我们便可以知道，如果知道 \(next[i-1]\) 为多少，便可以求出 \(next[i-1]\) 所有的候选项，从大到小分别为 \(next[i-1]\) ，\(next[next[i-1]]\) 等等，根据引理 \(3\) ，便可以知道 \(next[i]\) 可能的值应当为 \(next[i-1]\) 的所有的候选项分别加 \(1\) ，也就是说， \(next[i]\) 可能的值应当为 \(next[i-1]+1\) ， \(next[next[i-1]]+1\) 等等

注意：这里是可能的值，而不是候选项，原因是引理 \(3\) 的逆命题不成立

那么如何判断一个可能的值是否为答案呢？

还记得刚刚说的引理 \(3\) 的逆命题不成立吗，实际上只需要加上一个条件便成立了，就是末项相等（比如 \(B[next[i-1]+1]=B[i]\) 或 \(B[next[next[i-1]]+1]=B[i]\) 等等）

根据刚才的分析，可以写出以下代码

void get(char *s){
	nxt[1] = 0;//next数组被c++用过了，只好用nxt
	int len = strlen(s + 1);
	for (int i = 2,j = 0; i <= len; i++){//j = 0就是 j = nxt[1]
		while (j > 0 && s[i] != s[j+1]) j = nxt[j];
        //一开始的j必定为nxt[i-1]
        //j > 0防止死循环，表示从头开始
        //s[i] != s[j+1]，如果末项不同，继续向下找
		if (s[i] == s[j+1]) j++;
        //如果末项已经相同了，那么这是候选项，由于j是从大到小枚举的，所以这就是答案
        //加一不需要解释，这是递推式的一部分
		nxt[i] = j;
        //这里将nxt[i] = j与nxt[i] = 0巧妙地结合在了一起,也可以换一种写法
        //if (s[i] == s[j+1]) j++, nxt[i] = j;
        //else nxt[i] = 0;//匹配失败
	}
}
//用于获取next数组

//由于两步的定义类似，所以代码也差不多
for (int i = 1,j = 0; i <= n; i++){
	while (j > 0 && A[i] != B[j+1]) j = nxt[j];
	if (A[i] == B[j+1]) j++;
	if (j == m) //如果j恰好覆盖整个B数组，找到答案
}

经典题目：

【模板】KMP 字符串匹配 洛谷（模板）

Period UVA（思维+模板）