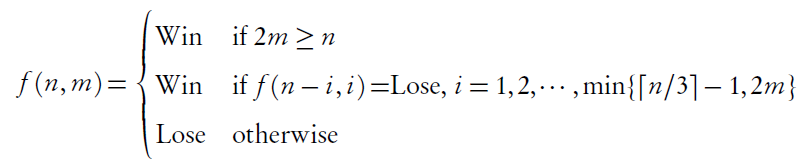Fibonacci Nim取子游戏

除了上一篇说过的Nim取子游戏以外，我还遇到过一道比较奇特的Nim取子游戏。这一问题的复杂程度远超过上一个问题的复杂程度。下面让我们来看看，对于这样的一类问题，我们该如何进行求解。（PDF版由此下载）

问题描述

有一堆 n 个石子，两个人轮流取石子，最后一个取完石子的人获胜。要求：

1. 第一次取石子时不能将所有石子取光。
2. 每一次至少取一个石子。
3. 每一次可以取的石子数不超过上一个人取的石子数的二倍。

求先手必败态构成的集合。

寻找思路

我们首先从较小的 n 开始尝试（为方便起见，我们记先手为A，后手为B，用状态 i 表示有 i 个石子）：

• 当 n=2 时： A取 1 个石子，到达状态 1；B取走 1 个石子。B获胜。即，先手必败。
• 当 n=3 时： 若一开始，A取 1 个石子，到达状态 2；B取走 2 个石子；B获胜。若一开始A取 2 个石子，则B取走 1 个石子；B获胜。即，先手必败。
• 当 n=4 时： 若一开始，A取 1 个石子，则B至多只能取 2 个石子，等同于当 n=3 时的A。因此，当 n=4 时，先手必胜。
• 当 n=5 时： 一开始，若A取 1 个石子，则B相当于 n=4 时的A，B必胜；一开始，若A取 2 个石子，则B可以将剩下的 3 个石子取光，B必胜。因此，当 n=5 时，先手必败。
• 当 n=6 时： 一开始，若A取 1 个石子，则B相当于 n=5 时的A，B必败；因此，当 n=6 时，先手必胜。

从上面的这些尝试中，我们可以总结出一个基本的规律：每次取石子时，若当前有 n 个石子，则至多可以取个石子，否则对方能够将剩下的石子全部取走。至于其他的规律，似乎并不显著，需要更多的实例继续观察。

此外，在尝试的过程中，我们还能发现额外的两个情况。

1. 原问题的子问题不仅与石子个数有关，还与上一个人取的石子个数有关。
2. 如果先手必败态具有显著的规律性的话，一定是因为有若干个“必败点”，一旦到达这些“必败点”，无论上一个人取了多少石子，轮到我们的时候都是必败的。

现在发现的信息还不足以纯粹的从数学上解决这一问题，我们不妨进行更多的尝试。鉴于这一问题实际上手工算起来挺麻烦，我们不妨先写个效率较低程序来算这个问题。

递归解

假设当前有 n 个石子，上一个人取了 m 个石子，则判断当前先走的人是输还是赢的函数可以递归地定义为下面这样：

按照这样的定义，我们很容易给出一个递归的程序，主要的程序片段如下：

int f(int n, int m)
{
    if(2 * m >= n) {
        return 1;
    }
    /* "(n + 2) / 3" in integer operation equals to
     * "ceiling(n / 3) - 1" in float operation.
     */
    int i = 1, bound = min((n + 2) / 3, 2 * m);
    for(; i <= bound; i++) {
        if(f(n - i, i) == 0) {
            return 1;
        }
    }
    return 0;
}

但是这个程序效率太低了，我用其计算的结果，就花了不少时间，计算结果如下（其中P表示先手必败，N表示先手必胜）：

P  P  P  N  P  N  N  P  N  N
1  2  3  4  5  6  7  8  9 10
N  N  P  N  N  N  N  N  N  N
11 12 13 14 15 16 17 18 19 20
P  N  N  N  N  N  N  N  N  N
21 22 23 24 25 26 27 28 29 30
N  N  N  P  N  N  N  N  N  N
31 32 33 34 35 36 37 38 39 40
N  N  N  N  N  N  N  N  N  N
41 42 43 44 45 46 47 48 49 50

似乎规律仍然不太显著，考虑改进我们的算法，以计算更多的情况。

动态规划解

不难看出，按照递归解中给出的递归定义进行计算，是有着很大量的重复计算的。这恰恰满足了动态规划解的两个条件：最优子结构和重叠子问题。

为了保持解形式上的优雅，不破坏递归结构，顺便也是偷个懒，这里给出一个使用备忘录（memoize）法¹的动态规划解。事实上，备忘录法的时间效率和一般的动态规划方法是一致的，只是比较浪费空间。下面给出部分代码。

int f(int n, int m)
{
    if(2 * m >= n) {
        return 1;
    }
    if(cache[n][m] != NAN) {
        return cache[n][m];
    }
    /* "(n + 2) / 3" in integer operation equals to
     * "ceiling(n / 3) - 1" in float operation.
     */
    int i = 1, bound = min((n + 2) / 3, 2 * m);
    for(; i <= bound; i++) {
        if(f(n - i, i) == 0) {
            return cache[n][m] = 1;
        }
    }
    return cache[n][m] = 0;
}

用其计算的先手必败态，得到结果：

  1   2   3   5   8  13  21  34  55  89
144 233 377 610 987

数学上的“紧致解”

通过观察计算结果，可以发现，先手必败态恰构成了Fibonacci数列。为叙述方便起见，如果一个数在Fibonacci数列中，我们称其为一个Fibonacci数。不妨猜测，对于，当且仅当 n 为一个Fibonacci数，有先手必败。

粗略的想一想，大概用数学归纳法可以证明这一结论。大概就是在Fibonacci数的石子数时，不能一次将石子数拿到剩余另一个Fibonacci数；而一个非Fibonacci数的石子数开始拿能一次将石子数拿到剩余一个Fibonacci数。下面我们按照这一思路证明之。

使用 f (k ) 表示第 k 个Fibonacci数，其中 f (0)=f (1)=1。将剩余石子数为 n 记为状态 n。若游戏处于状态 n，此时先手有必胜策略，则称状态 n 处于N状态；若此时后手有必胜策略，则称状态 n 处于P状态。（注意：一个状态处于P状态，当且仅当其按照游戏规则所能够到达的状态均为N状态；一个状态处于N状态，说明其能够按照游戏规则到达一个P状态。）

具体的证明过程，请见PDF版本的本文。更进一步的数学原理，请见参考资料2。

参考资料

1. 机械工业出版社《算法导论（原书第 2 版）》，第 15 章 动态规划，15.3 动态规划基础 做备忘录 P207。
2. EP8: Fibonacci Nim（斐波那契取石子博弈）