最长上升子序列

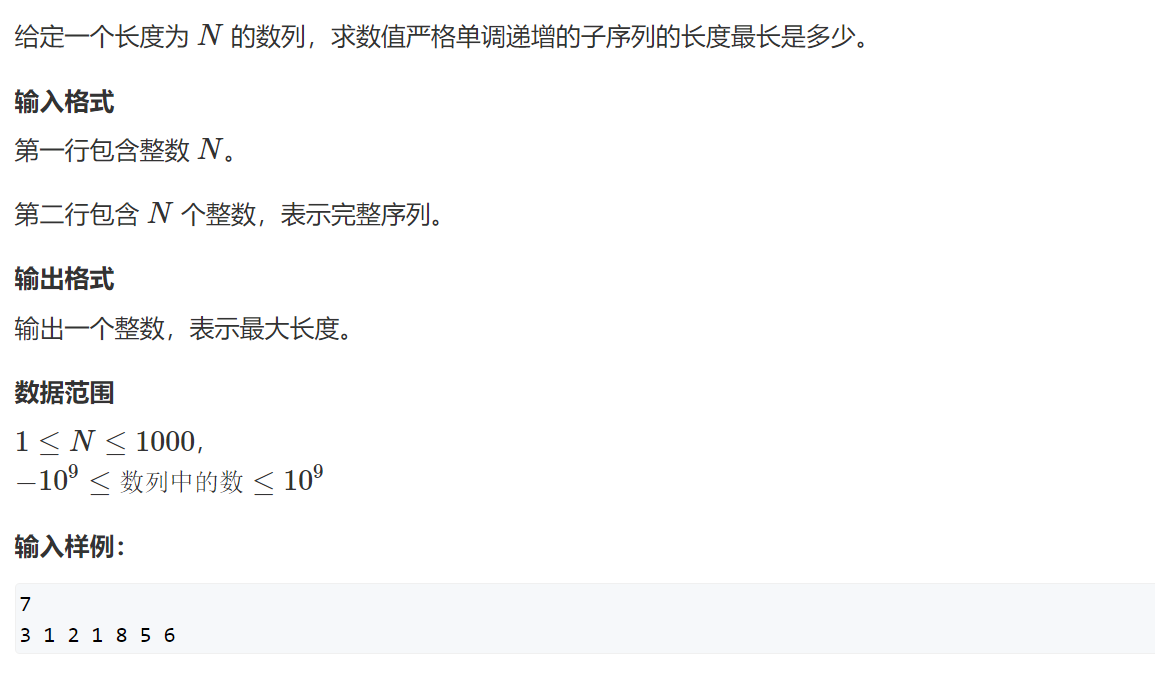
样例：3 1 2 1 8 5 6
那么最长上升子序列就是1 2 5 6
朴素解法，复杂度n^2:
我们构建一个数组f[n],f[i]储存的是前i个序列中比第i个数小的序列个数，我们通过max(f[i],f[j] + 1);不断继承较小的序列个数
code：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int w[N],f[N];

int main(){
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> w[i];
    int ans = 1;
    for (int i = 1; i <= n; i ++){
        f[i] = 1;
        for (int j = 1; j <= i;j ++){
            if (w[i] > w[j]) f[i] = max(f[i],f[j] + 1);
        }
        ans = max(ans,f[i]);
    }
    cout << ans;
    return 0;
}

解法二：
n^2 的复杂度是绝对不能接受的，下面我们用二分来优化
这里我们构建的f[n]就是我们要求的最长上升子序列
如果a[i] > f[cnt] 我们就加到f数组最后，让f[++cnt] = a[i],否则的话，我们二分查找，找出f[n]中小于a[i]的数的下标x,让f[x] = a[i]；
code:

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int a[N],f[N];

int cnt;

int find(int x){
    int l = 1, r = cnt;
    while(l < r){
        int mid = l + r >> 1;
        if(f[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main(){
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
        
    f[++cnt] = a[1];
    
    for (int i = 2; i <= n; i ++){
        if(a[i] > f[cnt]) f[++cnt] = a[i];
        else{
            int t = find(a[i]);
            f[t] = a[i];
        }
    }
    cout << cnt;
}