https://atcoder.jp/contests/agc039/tasks/agc039_f
由于难以直接计数,我们不妨虑容斥。假设我们枚举了每一行、每一列的最小值分别是什么,那么可以算出这种情况的贡献为\prod_{i=1}^{n}\prod_{j=1}^{m}{max\{a[i],b[j]\}}。而计算方案数可以枚举哪些列、哪些行上是强制不能满足条件的,也就是a[i]或b[i]加1。这部分可以看代码1。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long int ll; 4 const int maxn=105; 5 ll n,m,K,mod,f[maxn][maxn][maxn],C[maxn][maxn]; 6 ll fac[maxn],inv[maxn]; 7 inline ll qpow(ll x,ll y) 8 { 9 ll ans=1,base=x; 10 while(y) 11 { 12 if(y&1) 13 ans=ans*base%mod; 14 base=base*base%mod; 15 y>>=1; 16 } 17 return ans; 18 } 19 inline void init() 20 { 21 fac[0]=1; 22 for(int i=1;i<=100;++i) 23 fac[i]=fac[i-1]*i%mod; 24 for(int i=0;i<=100;++i) 25 inv[i]=qpow(fac[i],mod-2); 26 C[0][0]=1; 27 for(int i=1;i<=100;++i) 28 { 29 C[i][0]=1; 30 for(int j=1;j<=i;++j) 31 C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; 32 } 33 } 34 int a[55],b[55]; 35 ll ans; 36 inline ll get() 37 { 38 ll s=0; 39 for(int s1=0;s1<(1<<n);++s1) 40 for(int s2=0;s2<(1<<m);++s2) 41 { 42 ll g=1; 43 for(int i=1;i<=n;++i) 44 for(int j=1;j<=m;++j) 45 { 46 bool fx=(s1&(1<<(i-1)))>0; 47 bool fy=(s2&(1<<(j-1)))>0; 48 int x=a[i],y=b[j]; 49 x+=fx,y+=fy; 50 g=g*(K+1-max(x,y))%mod; 51 } 52 for(int i=0;i<n;++i) 53 if(s1&(1<<i)) 54 g=-g; 55 for(int i=0;i<m;++i) 56 if(s2&(1<<i)) 57 g=-g; 58 s=(s+g)%mod; 59 } 60 return s; 61 } 62 void dfs(int s,int d) 63 { 64 if(s==n+m+1) 65 { 66 ll g=1; 67 for(int i=1;i<=n;++i) 68 for(int j=1;j<=m;++j) 69 g=g*min(a[i],b[j])%mod; 70 ans=(ans+g*get())%mod; 71 return; 72 } 73 if(s<=n) 74 for(int i=1;i<=K;++i) 75 { 76 a[s]=i; 77 if(i&1) 78 dfs(s+1,d); 79 else 80 dfs(s+1,-d); 81 } 82 else 83 for(int i=1;i<=K;++i) 84 { 85 b[s-n]=i; 86 if(i&1) 87 dfs(s+1,d); 88 else 89 dfs(s+1,-d); 90 } 91 } 92 inline void solve() 93 { 94 dfs(1,1); 95 cout<<ans<<endl; 96 } 97 int main() 98 { 99 ios::sync_with_stdio(false); 100 cin>>n>>m>>K>>mod; 101 init(); 102 solve(); 103 return 0; 104 }
注意到我们只关心相对的大小关系,并不关心它们之间具体的位置,并且在暴力计算中所有的贡献都可以看成是“独立”的。我们设f[i][j][k]为填了大小为i*j的方格,并且最大的数已经填到k(当然,可以不填),我们枚举不被容斥的行数i1、被容斥的行数i2、不被容斥的列数j1、被容斥的列数j2。容斥系数显然为(-1)^(i2+j2),其它的转移系数可以通过画图的方法来得知(或者你可以看下面的图)。这部分可以看代码2。复杂度是七次方的。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long int ll; 4 const int maxn=105; 5 ll n,m,K,mod,f[maxn][maxn][maxn],C[maxn][maxn]; 6 ll fac[maxn],inv[maxn]; 7 inline ll qpow(ll x,ll y) 8 { 9 ll ans=1,base=x; 10 assert(y>=0); 11 while(y) 12 { 13 if(y&1) 14 ans=ans*base%mod; 15 base=base*base%mod; 16 y>>=1; 17 } 18 return ans; 19 } 20 inline void init() 21 { 22 fac[0]=1; 23 for(int i=1;i<=100;++i) 24 fac[i]=fac[i-1]*i%mod; 25 for(int i=0;i<=100;++i) 26 inv[i]=qpow(fac[i],mod-2); 27 C[0][0]=1; 28 for(int i=1;i<=100;++i) 29 { 30 C[i][0]=1; 31 for(int j=1;j<=i;++j) 32 C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; 33 } 34 } 35 inline void add(ll&x,ll y) 36 { 37 x=(x+y)%mod; 38 } 39 inline void solve() 40 { 41 f[0][0][0]=1; 42 for(int k=0;k<K;++k) 43 for(int i=0;i<=n;++i) 44 for(int j=0;j<=m;++j) 45 if(f[i][j][k]) 46 for(int i1=0;i1+i<=n;++i1) 47 for(int j1=0;j1+j<=m;++j1) 48 for(int i2=0;i1+i+i2<=n;++i2) 49 for(int j2=0;j1+j+j2<=m;++j2) 50 { 51 ll s1=inv[i1]%mod*inv[i2]%mod*inv[j1]%mod*inv[j2]%mod; 52 ll s2=qpow(K+1-(k+2),(i+i1+i2)*j2+(j+j1+j2)*i2-i2*j2); 53 ll s3=qpow(K+1-(k+1),(i+i1)*j1+(j+j1)*i1-i1*j1); 54 ll s4=qpow(k+1,(n-i)*(j1+j2)+(m-j)*(i1+i2)-(i1+i2)*(j1+j2)); 55 if((i2+j2)&1) 56 add(f[i+i1+i2][j+j1+j2][k+1],-f[i][j][k]*s1%mod*s2%mod*s3%mod*s4%mod); 57 else 58 add(f[i+i1+i2][j+j1+j2][k+1],f[i][j][k]*s1%mod*s2%mod*s3%mod*s4%mod); 59 } 60 ll ans=f[n][m][K]*fac[n]%mod*fac[m]%mod; 61 ans=(ans%mod+mod)%mod; 62 cout<<ans<<endl; 63 } 64 int main() 65 { 66 ios::sync_with_stdio(false); 67 cin>>n>>m>>K>>mod; 68 init(); 69 solve(); 70 return 0; 71 }
实际上,我们发现转移系数只和“面积”有关,因此我们对于枚举的四个系数可以分开来考虑。
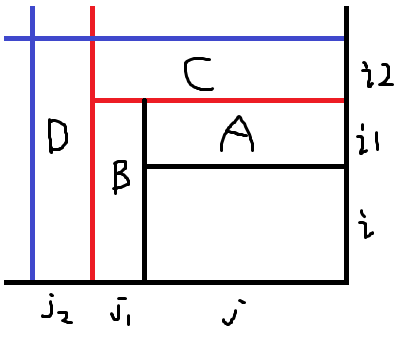
具体来讲,转移时先枚举区域A,转移系数为(K+1-(k+1))^A的面积;接着枚举区域B,转移系数为(K+1-(k+1))^B的面积;接着枚举区域C,转移系数为(K+1-(k+2))^C的面积*(-1)^C的面积;接着枚举区域D,转移系数为(K+1-(k+2))^D的面积*(-1)^C的面积。这个是方案数的系数,而价值的系数就是(k+1)^(左坐标(i,j)左上角且不在左边(i+i1+i2,j+j1+j2)左上的面积)。预处理所有需要用到的i^k,复杂度四次方。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long int ll; 4 const int maxn=105; 5 ll n,m,K,mod,f[maxn][maxn][maxn],C[maxn][maxn],pre[maxn][maxn*maxn]; 6 ll tmp1[maxn][maxn],tmp2[maxn][maxn]; 7 ll fac[maxn],inv[maxn]; 8 inline ll qpow(ll x,ll y) 9 { 10 ll ans=1,base=x; 11 assert(y>=0); 12 while(y) 13 { 14 if(y&1) 15 ans=ans*base%mod; 16 base=base*base%mod; 17 y>>=1; 18 } 19 return ans; 20 } 21 inline void init() 22 { 23 fac[0]=1; 24 for(int i=1;i<=100;++i) 25 fac[i]=fac[i-1]*i%mod; 26 for(int i=0;i<=100;++i) 27 inv[i]=qpow(fac[i],mod-2); 28 C[0][0]=1; 29 for(int i=1;i<=100;++i) 30 { 31 C[i][0]=1; 32 for(int j=1;j<=i;++j) 33 C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; 34 } 35 for(int k=0;k<=K+2;++k) 36 { 37 pre[k][0]=1; 38 for(int i=1;i<=n*m;++i) 39 pre[k][i]=pre[k][i-1]*k%mod; 40 } 41 } 42 inline void add(ll&x,ll y) 43 { 44 x=(x+y)%mod; 45 } 46 inline void solve() 47 { 48 f[0][0][0]=1; 49 for(int k=0;k<K;++k) 50 { 51 memset(tmp1,0,sizeof(tmp1)); 52 for(int i=0;i<=n;++i) 53 for(int j=0;j<=m;++j) 54 for(int i1=0;i1+i<=n;++i1) 55 add(tmp1[i+i1][j],f[i][j][k]*inv[i1]%mod*pre[K+1-(k+1)][i1*j]%mod*pre[k+1][(m-j)*i1]); 56 memset(tmp2,0,sizeof(tmp2)); 57 for(int i=0;i<=n;++i) 58 for(int j=0;j<=m;++j) 59 for(int j1=0;j1+j<=m;++j1) 60 add(tmp2[i][j+j1],tmp1[i][j]*inv[j1]%mod*pre[K+1-(k+1)][j1*i]%mod*pre[k+1][(n-i)*j1]); 61 memset(tmp1,0,sizeof(tmp1)); 62 for(int i=0;i<=n;++i) 63 for(int j=0;j<=m;++j) 64 for(int i2=0;i2+i<=n;++i2) 65 if(i2&1) 66 add(tmp1[i+i2][j],-tmp2[i][j]*inv[i2]%mod*pre[K+1-(k+2)][i2*j]%mod*pre[k+1][(m-j)*i2]); 67 else 68 add(tmp1[i+i2][j],tmp2[i][j]*inv[i2]%mod*pre[K+1-(k+2)][i2*j]%mod*pre[k+1][(m-j)*i2]); 69 memset(tmp2,0,sizeof(tmp2)); 70 for(int i=0;i<=n;++i) 71 for(int j=0;j<=m;++j) 72 for(int j2=0;j2+j<=m;++j2) 73 if(j2&1) 74 add(tmp2[i][j+j2],-tmp1[i][j]*inv[j2]%mod*pre[K+1-(k+2)][j2*i]%mod*pre[k+1][(n-i)*j2]); 75 else 76 add(tmp2[i][j+j2],tmp1[i][j]*inv[j2]%mod*pre[K+1-(k+2)][j2*i]%mod*pre[k+1][(n-i)*j2]); 77 for(int i=0;i<=n;++i) 78 for(int j=0;j<=m;++j) 79 f[i][j][k+1]=tmp2[i][j]; 80 } 81 ll ans=f[n][m][K]*fac[n]%mod*fac[m]%mod; 82 ans=(ans%mod+mod)%mod; 83 cout<<ans<<endl; 84 } 85 int main() 86 { 87 ios::sync_with_stdio(false); 88 cin>>n>>m>>K>>mod; 89 init(); 90 solve(); 91 return 0; 92 }

 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号