Codeforces Round #419 (Div. 1)

Codeforces Round #419 (Div. 1)

Karen and Game

题目描述

在回校的路上，Karen沉迷于她手机上的游戏。
游戏是这样玩的：在每一关，有一个\(n \times m\)的网格。每一格都有一个数字\(0\)，每一步选择一行或者一列，将该行或列的格子里的数全部加\(1\)。要赢这个游戏，必须在所有操作完成后，在第i行第j列格子里的数字必须等于\(g_{(i,j)}\)。
Karen在一关卡住了，她想知道一个用最少步数赢这个游戏的方法。请帮助她完成这个任务。

solution

贪心。操作的顺序是不影响答案的。注意如果\(m>n\),那么先处理行，否则先处理列。
时间复杂度：\(O(nm)\)

Karen and Test

题目描述

有\(n\)个整数写在一行，Karen必须交替地将相邻的两个整数做加法和减法，并把答案写在下一行，她必须重复这个步骤直至只剩下一个整数，第一个操作必须是加法。
注意：如果她在上一行的最后一行操作是加法，那么下一行的第一个操作必须是减法，相反时类似。

solution

这题是找规律。。。
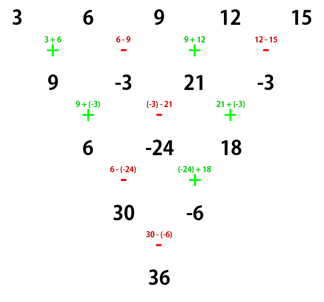
加减法交替，考虑可能跟\(n\)的奇偶性有关，考虑\(n\)是偶数（若\(n\)是奇数，则暴力进行一次操作使它变为偶数，因为数的个数为奇数的行（简称奇数行）的下一行第一个运算还是加法）。因为\(n\)比较大，所以我们考虑把每个数对最终答案的贡献算出来。
例如样例：3 7 5 2

如果我们隔一行来看，只看第一行和第三行，我们发现第三行的第一个数等于第一行的第一个数加第三个数，第三行第二个数等于第一行第二个数加第四个数，这是因为偶数行的下一行的第一个运算是减法，这样会把偶数行相邻三个数中间的那个消掉，所以第二个偶数行（也就是第三行）第一个数为\(3+5\)，第二个数为\(7+2\)，如果第一行后面还有两个数\(4,6\)，那么第三个数为\(5+4\)，第四个数为\(2+6\)，如下

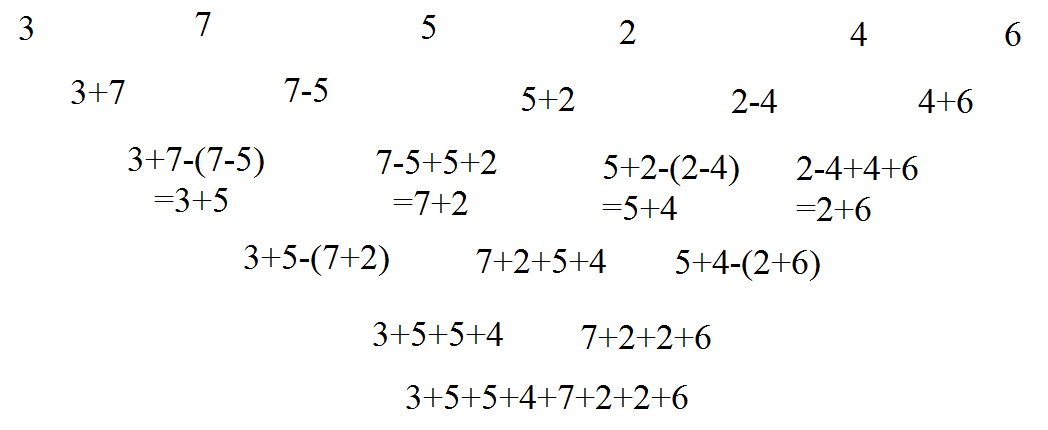
那么我们就可以将奇数项与偶数项分开考虑，那问题就转化为给出一行\(m\)个数，每次将相邻的两个数相加写在下一行，问最后的答案。这个问题就简单多了，显然第k项对答案的贡献为\(C_{(m-1)}^{(k-1)}\).
再看这题，虽然\(n=4和n=6\)都是偶数，但\(n=4\)时最后一个运算是减法，\(n=6\)时最后一个运算是加法，可以推测：当\(n\)为\(4\)的倍数时，最后一个运算是减法，\(n\)除以\(4\)余\(2\)时，最后一个运算为加法。可得到答案的计算式：
\(n为4\)的倍数时:

$$\sum_{k为奇数}^{k \leq n} C_{\left \lfloor \frac{n}{2}-1 \right \rfloor}^{\left \lfloor \frac{k-1}{2} \right \rfloor} a[k]-\sum_{k为偶数}^{k \leq n} C_{\left \lfloor \frac{n}{2}-1 \right \rfloor}^{\left \lfloor \frac{k-1}{2} \right \rfloor} a[k]$$

\(n\)除以\(4\)余\(2\)时：

$$\sum_{k}^{k \leq n} C_{\left \lfloor \frac{n}{2}-1 \right \rfloor}^{\left \lfloor \frac{k-1}{2} \right \rfloor} a[k]$$

时间复杂度：\(O(nlog(10^9+7))\)

Karen and Supermarket

题目描述

在回家的路上，Karen想去超市买些东西。
她想买很多东西，但因为她是一个学生，所以她的预算很受限，事实上，她最大只能用\(b\)元。超市在卖\(n\)种商品，第\(i\)种商品需要\(c_i\)元，当然每种商品只能买一个。最近，超市想增加他们的营业额，Karen作为一个老顾客可以拿到\(n\)张优惠券，如果她想买第\(i\)种商品，她可以使用第\(i\)张优惠券来使价格降低\(d_i\)元。当然如果没有买这种商品就不能使用对应的优惠券。
但是，优惠券的使用还有一个条件，对于第\(i(i\geq2)\)张优惠券，如果要使用它，则必须要使用第\(x_i\)张优惠券，也就是说如果要用一张优惠券，可能同时要用很多张。
Karen想知道她最多能买多少种商品。

solution

一道树形背包，由于钱的范围太大，所以状态\(f[i][j][k]\)为在以\(i\)为根的子树下买\(j\)种商品最少要多少钱，当\(k=0\)时不用优惠券，当\(k=1\)时用优惠券。转移的方程也很简单，问题在于时间复杂度，设以\(i\)为根的子树的大小为\(size[i]\)，则时间复杂度为\(\sum_{i=1}^n size[i]^2\)，当树退化为一条链时，时间复杂度会退化为\(n^3\)。这时就需要一些小优化。可以模仿启发式合并，将背包的数组初始化为最大的儿子，则时间复杂度变为\(\sum_{i=1}^n size[i](size[i]-maxson)\)，可以证明该时间复杂度最大为\(O(n^2 logn)\)(完全二叉树时最大)
还有一个方法，就是缩小枚举的范围。假设要把第\(i\)个儿子加入背包，当前已经加入的儿子的节点总数为\(sum\),那么背包大小只需枚举到\(sum+size[i]\)即可，这样时间复杂度就相等于是点对对数，也就是\(O(n^2)\)

Karen and Cards

题目描述

有一种卡牌，卡牌有三种属性：力量\(a_i\)，防御\(b_i\)，速度\(c_i\),力量的最大值是\(p\)，防御的最大值是\(q\)，速度的最大值是\(r\)。如果一张卡牌至少有两种属性比另一张卡牌大，那么这张卡牌就可以打败另一张卡牌。现在有\(n\)张卡牌,问有多少张卡牌可以打败这\(n\)张牌。

solution

假设\(p = q = r = 5\),有两张牌：\((4, 2, 3), (2, 3, 4)\)
我们尝试用图来表示卡牌

绿色为能打败所有牌的牌。可以注意到：当\(c\)递增时，每个\(a\)对应的\(b\)是递减的，这很好理解，\(c\)变大了，有一些牌就可以借助\(c\)来打败别的牌，\(b\)自然变小。同样可以看到的是，当\(c\)一定时，\(a\)越大，\(b\)越小。可以考虑求问题的补集，然后从大到小枚举速度\(i\)，算出速度等于\(i\)的牌，有多少张不能打败\(n\)张牌。可以维护一个数组\(maxb\)，\(maxb[i]\)表示，当\(a=i\)时，最大的不能打败所有牌的\(b\)是\(maxb[i]\)。
在不断枚举的同时用\(n\)张牌中速度等于\(i\)的牌更新\(maxb\)。假设是先更新，后算答案，因为是从大到小枚举，所以当前枚举的卡牌的速度这一属性不能打败所有卡牌，所以如果还有另一属性不能打败所有卡牌，那么这张牌就不能打败所有卡牌，假设用卡牌\(j\)来更新数组\(maxb\)，那么\([0, a_j]\)可更新为\(q\)，\([a_j+1, p]\)可更新为\(b_j\)，这里可以用线段树来维护这个数组，但有一个问题：有可能更新的区间的某些位置原来的数比现在更新的值大，这样线段树就很难处理了。但这题有一个规律，就是上面说的：当\(c\)一定时，\(a\)越大，\(b\)越小。那么就可以利用线段树找出需要更新的区间的开始位置在哪里，再进行更新。
时间复杂度：\(O(nlogn)\)

Karen and Neighborhood

题目描述

在数轴上有\(n\)个点（从\(1\)到\(n\)标号），相邻两个点的距离相等。先以此选择这\(n\)，每次选择没选过的，并且与选过的点距离最近的最远的点，如果有多个这样的点，就选编号最小的那个，问第\(k\)个选择的点是哪个。

solution

这题的规律实在是太强了。。。
首先第一个选的肯定是\(1\)，第二个选的肯定是\(n\)。
除去这两个点，我们可以吧剩下的点看成是长度为\(n-2\)的线段，每次选线段中间的点，然后长度减一，并分成两半。

注意到一些规律：
1.每层的数字最多有两种，而且只相差\(1\)。
2.设某层较小的数字为\(l\)，如果\(l\)为奇数，则从左到右选数，如果\(l\)是偶数，则先把\(l+1\)的从左到右选完，再把\(l\)从左到右选完。
如果某一层只有一种数字，或者\(l\)为奇数，那么就很简单了，问题是\(l\)为偶数怎么办，怎么知道\(l+1\)的位置呢？
观察一下，当\(n-2=39 \text ~ 47\)时，第四行的变化：

• 39: 4, 4, 4, 4, 4, 4, 4, 4
• 40: 4, 4, 4, 4, 4, 4, 4, 5
• 41: 4, 4, 4, 5, 4, 4, 4, 5
• 42: 4, 4, 4, 5, 4, 5, 4, 5
• 43: 4, 5, 4, 5, 4, 5, 4, 5
• 44: 4, 5, 4, 5, 4, 5, 5, 5
• 45: 4, 5, 5, 5, 4, 5, 5, 5
• 46: 4, 5, 5, 5, 5, 5, 5, 5
• 47: 5, 5, 5, 5, 5, 5, 5, 5

观察一下\(5\)出现的位置顺序：（从\(0\)开始编号）

• 7:111
• 3:011
• 5:101
• 1:001
• 6:110
• 2:010
• 4:100
• 0:000

这正好是\(7\text ~ 0\)的二进制翻转后对应的数字。
假设\(n-2=44\)，要找的数正好是第四层的第五个数，

• 7:111
• 3:011
• 5:101
• 1:001
• 6:110

也就是说，要在这\(5\)个数里找出第\(5\)小的数，可以用逐位猜数求得：
最高位是\(0\)的只有\(2\)个，所以最高位应该是\(1\)，\(1??\)，删去最高位,找剩下数字里第\(3\)小的数

• 7:11
• 5:01
• 6:10

最高位是\(0\)的只有\(1\)个，所以第二位是\(1\)，\(11?\)，删去最高位，找剩下数字里第\(2\)小的数

• 7:1
• 6:0

最高位是\(0\)的只有\(1\)个，所以第三位是\(1\)，\(111\).
那么怎么知道每一位有多少个\(0\)呢？注意到数字是由从大到小的数二进制翻转得来的，所以最高位\((0, 1)\)各占一半，或者\(1\)比\(0\)多一个，把最高位相同的数以次放在一起，去掉最高位，分开两堆看，依然有这样的规律。
如果要找的数超过了当前层\(l+1\)的个数，那方法是差不多的。
看上去好像问题解决了，但是。。。
有两种边界：\(l=1\)和\(l=2\)
当\(l=1\)时，\(2\)要看成是两个点
当\(l=3\)时，先处理\(3\)，处理后剩下\(1,2\)，就按\(l=1\)时处理。
时间复杂度：\(O(logn)\)