NOI2012 Day1

NOI2012 Day1

随机数生成器

题目描述：给出数列\(X_{n+1}=(aX_n+c)mod m\),求\(X_n mod g\)

solution：
矩阵乘法，但数有可能在运算时爆\(long long\)，可以将一个数拆成两个\(long long\)存储，也可以用大数乘法\((b*c)mod m\)：

LL get_mod(LL b, LL c)
{
	LL ans=0;
	while (b)
	{
		if (b & 1) ans=(ans+c)%m;
		c=c*2%m;
		b>>=1;
	}
	return ans;
}

时间复杂度：\(O(n)\)或\(O(nlogn)\)

骑行川藏

题目描述：给出\(n\)段路，每段路有三个参数\(s_i, k_i, v_i'\)，分别表示这段路的长度，风阻系数以及风速，若某段路用匀速\(v\)通过，则受到的风阻的大小为\(F=k_i(v-v_i')^2\),消耗能量为\(E=k_i(v-v_i')^2s_i\),保证\(\sum_{i=1}^n E \leq E_U\)的前提下，求最短时间。

solution:
虽然在同一段路上的速度可以随时变化，但从微积分的角度分析，这是没必要的，他可以对应一个匀速的方案，所以每一段路应该各自匀速。设第\(i\)段路的速度为\(v_i\),为题转化为：

\[\sum_{i=1}^n k_i(v_i-v_i')^2s_i \leq E_U,求lim \sum_{i-1}^n \frac{s_i}{v_i} \]

运用贪心思想，不等式取等是最好的。

\[\sum_{i=1}^n k_i(v_i-v_i')^2s_i = E_U,求lim \sum_{i-1}^n \frac{s_i}{v_i} \]

把\(v_i\)看成\(n\)个变量，则约束条件为\(g\)，目标函数为\(f\)

\[g(v_1, v_2, \cdots, v_n)=\sum_{i=1}^n k_i(v_i-v_i')^2s_i=E_U \]

\[f(v_1, v_2, \cdots, v_n)=\sum_{i=1}^n \frac{s_i}{v_i} \]

拉格朗日乘数法

\[\frac{s_i}{v_i^2}=\lambda k_is_i \cdot 2(v_i-v_i') \]

\[\frac{1}{\lambda}=2k_iv_i^2(v_i-v_i') \]

二分\(2k_iv_i^2(v_i-v_i')\),因为\(v_i>0\)，所以该函数递增，二分可求出\(v_i\),判断是否满足约束条件，若满足，则求到最优解。

时间复杂度：\(?\)（难以计算， 精度要求高）

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <deque>
#include <queue>
#include <vector>
#include <map>
#include <complex>
using namespace std;

const int maxn=int(1e4)+100;
const double eps=1e-10;

int n;
double E, lambda;
double s[maxn], k[maxn], vf[maxn], v[maxn];
double ans;

void init()
{
	scanf("%d%lf", &n, &E);
	for (int i=1; i<=n; ++i)
		scanf("%lf%lf%lf", &s[i], &k[i], &vf[i]);
}
void calc_v()
{
	for (int i=1; i<=n; ++i)
	{
		double L=0, R=1e4;
		while (L<R)
		{
			double mid=(L+R)/2;
			double tmp=2*k[i]*mid*mid*(mid-vf[i]);
			if (fabs(tmp-lambda)<eps)
			{
				v[i]=mid;
				break;
			}
			if (tmp<lambda) L=mid; else R=mid;
		}
	}
}
bool check()
{
	double tmp=0;
	for (int i=1; i<=n; ++i)
		tmp+=k[i]*(v[i]-vf[i])*(v[i]-vf[i])*s[i];
	return tmp<=E;
}
double calc_ans()
{
	double tmp=0;
	for (int i=1; i<=n; ++i)
		tmp+=s[i]/v[i];
	return tmp;
}
void solve()
{
	double L=0, R=1e5;
	while (L+eps<R)
	{
		lambda=(L+R)/2;
		calc_v();
		if (check()) L=lambda; else R=lambda;
	}
	lambda=L;
	calc_v();
	ans=calc_ans();
}
int main()
{
	freopen("bicycling.in", "r", stdin);
	freopen("bicycling.out", "w", stdout);
	init();
	solve();
	printf("%lf", ans);
	return 0;
}

魔幻棋盘

题目描述：给出一个矩阵与其中的一个格\(P(x, y)\)，支持两种操作：1、询问子矩阵的最大公约数，子矩阵包含\(P\). 2、让子矩阵加上一个整数。

solution：
恶心的处理题。
对于任意的两个数，它们的最大公约数等于它们的差与其中一个数求最大公约数。而且询问一定包含\(P\)，所以可以采用作差的方法。如图：


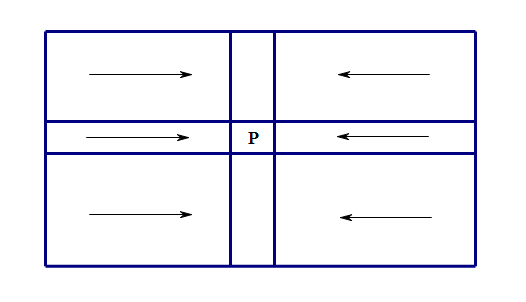
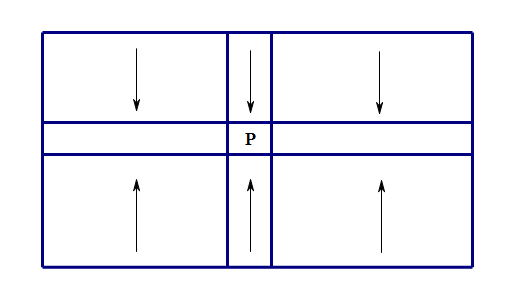
因为询问一定包含\(P\)，所以可以向内（\(P\)），作差，使得每个数与内相关，图中为箭头尾减头，只是相邻格子作差，先做图一，处理好图一后，用结果作差，即图二所示，也只是相邻格子作差。所以图一和图二作差时都要按箭头方向枚举。
将作差后的最后结果用二维线段树优化，询问时直接在二维线段树询问最大公约数，然后再跟\(P\)求一下就可以了。
如果没有修改，这题就算是做完了，但现在有修改，作差法就展现出它的优势了。因为不可能对整段数的最大公约数进行修改，作差法给予了单点修改的可能。
首先对于一个修改，有四个位置是一定要改的。

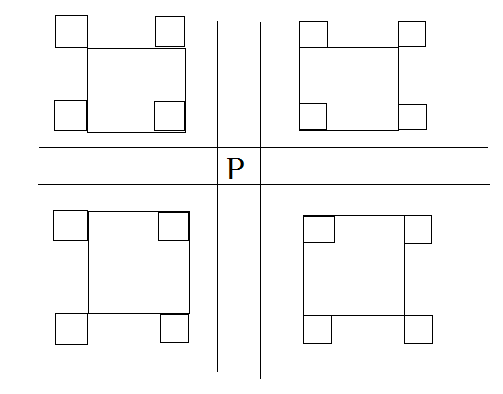
图中表示的是如果整个矩形都在一个象限，那么要修改哪些点，如果跨象限了，那么就要判断四个角的点在哪个象限。矩形覆盖了\(P\)的行或列的，也要对相应位置进行修改。

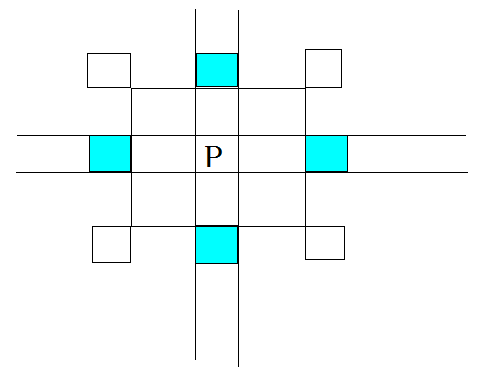
这里的处理比较恶心，自行脑补。