摘要:
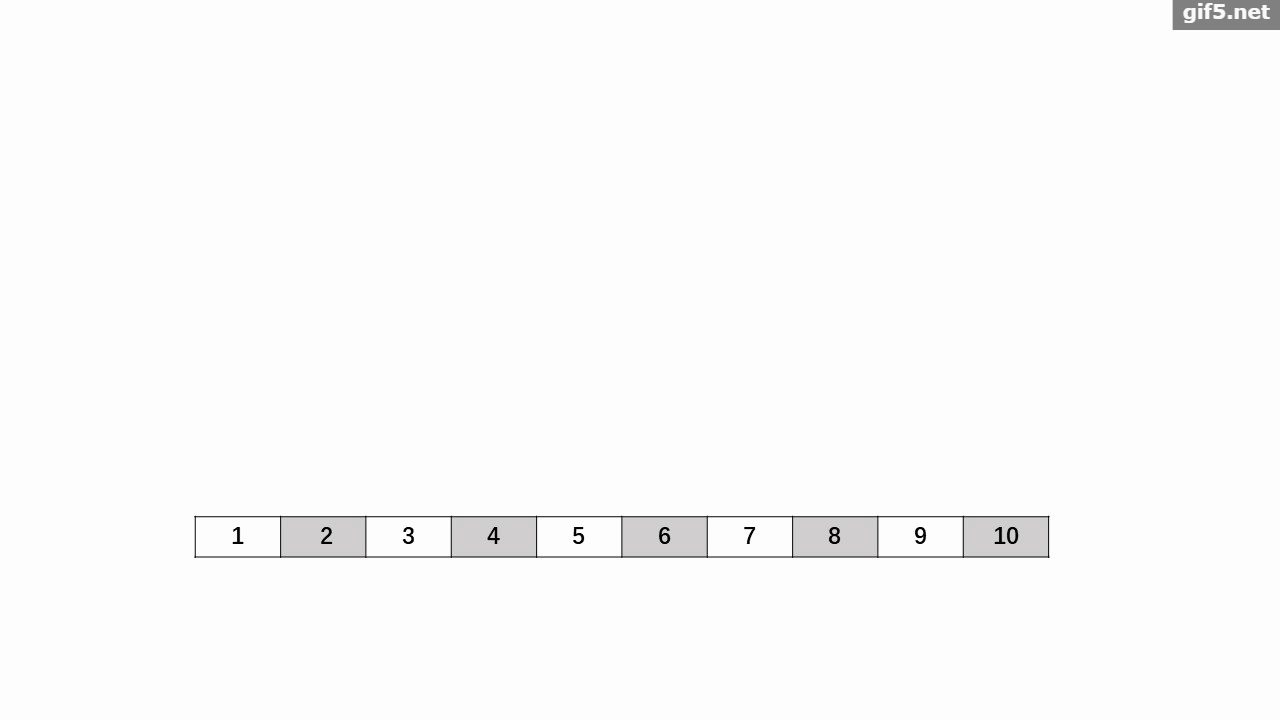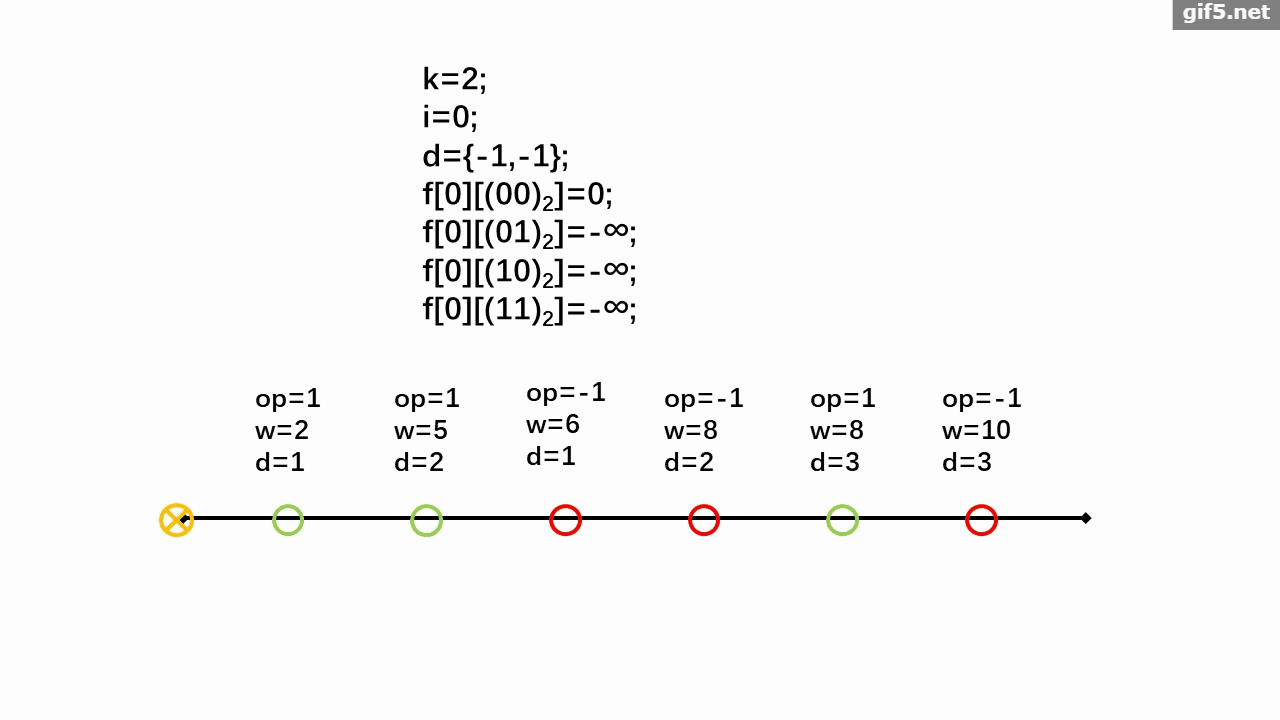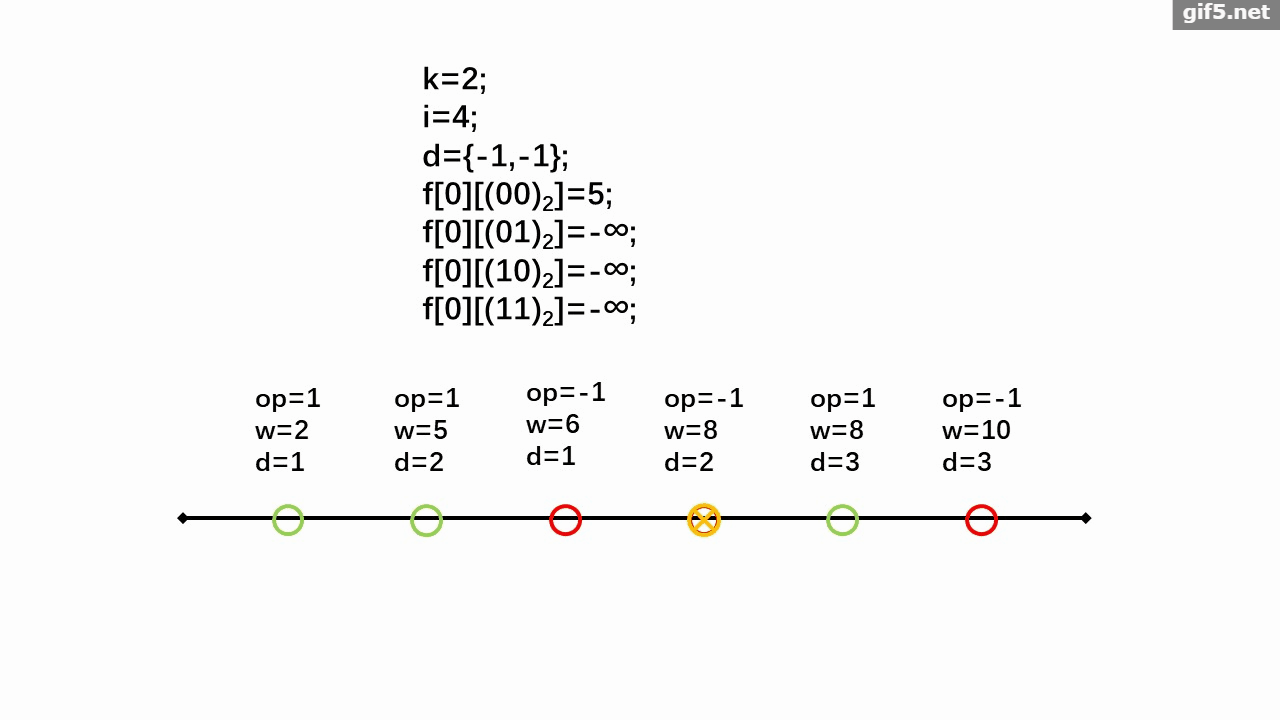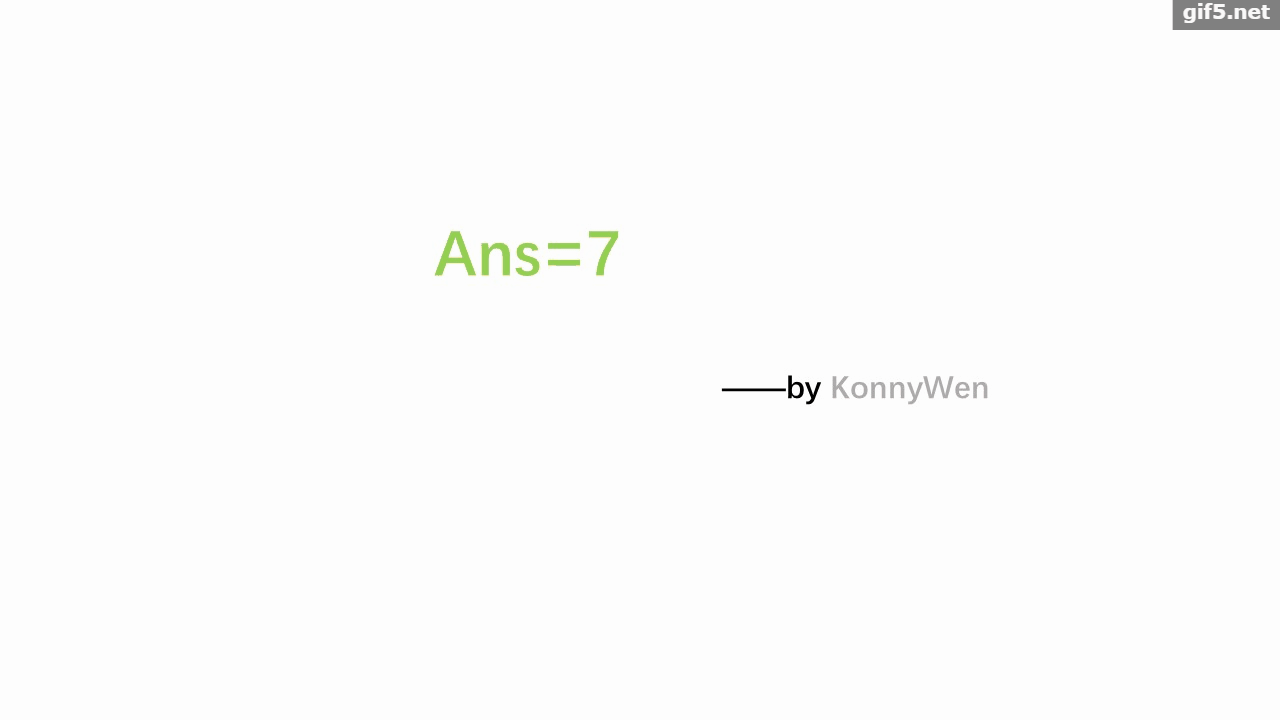 给定 $n$,$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作,每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次(可以不用)。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围:$1\le n\le 10^5$,$1\le m\le 10^9$,$1\le k\le 8$。
阅读全文
给定 $n$,$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作,每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次(可以不用)。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围:$1\le n\le 10^5$,$1\le m\le 10^9$,$1\le k\le 8$。
阅读全文
 给定 $n$,$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作,每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次(可以不用)。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围:$1\le n\le 10^5$,$1\le m\le 10^9$,$1\le k\le 8$。
阅读全文
给定 $n$,$m$ 和 $k$。有一个序列 $a\{m\}$ 初始值为 $0$。有 $n$ 种操作,每种可以使 $[L_i,R_i]$ 区间序列值 $+1$。每个操作最多用 $1$ 次(可以不用)。保证对于每个 $i(1\le i\le n)$ 最多存在 $k$ 个不同的 $j$ 满足 $i\in[L_j,R_j]$。求最后的序列中奇数最多个数。
数据范围:$1\le n\le 10^5$,$1\le m\le 10^9$,$1\le k\le 8$。
阅读全文
posted @ 2020-04-07 17:14
George1123
阅读(263)
评论(0)
推荐(1)

 给定 $n$ 和 $m$ 以及序列 $a\{n\}$。有 $m$ 次询问,每次给定区间 $[l,r]\in[1,n]$,求 $$\sum_{l\le l'\le r'\le r}\min_{i=l'}^{r'}a_i$$
数据范围:$1\le n,m\le 10^5$,$|a_i|\le 10^9$。
给定 $n$ 和 $m$ 以及序列 $a\{n\}$。有 $m$ 次询问,每次给定区间 $[l,r]\in[1,n]$,求 $$\sum_{l\le l'\le r'\le r}\min_{i=l'}^{r'}a_i$$
数据范围:$1\le n,m\le 10^5$,$|a_i|\le 10^9$。
 蒟蒻的 $\texttt{FST}$ 大赛题解。
蒟蒻的 $\texttt{FST}$ 大赛题解。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号