摘要：
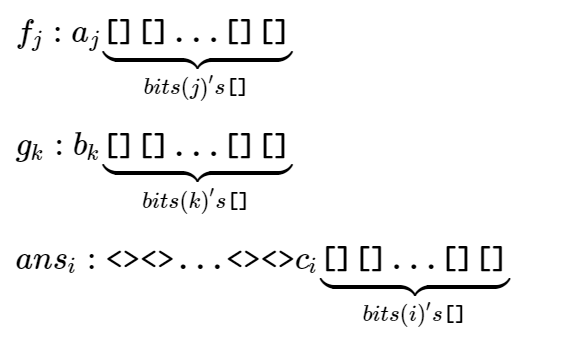给定 $n$ 和序列 $a_0,a_1,\dots,a_{2^n-1}$ 和 $b_0,b_1,\dots,b_{2^n-1}$，求序列 $c_0,c_1,\dots,c_{2^n-1}$ 满足 $$c_i=\left(\sum_{j|k=i,j\&k=0} a_j\cdot b_k\right)\bmod 4$$ 数据范围：$a_i,b_i\in[0,3]$，$0\le n\le 21$。
阅读全文
给定 $n$ 和序列 $a_0,a_1,\dots,a_{2^n-1}$ 和 $b_0,b_1,\dots,b_{2^n-1}$，求序列 $c_0,c_1,\dots,c_{2^n-1}$ 满足 $$c_i=\left(\sum_{j|k=i,j\&k=0} a_j\cdot b_k\right)\bmod 4$$ 数据范围：$a_i,b_i\in[0,3]$，$0\le n\le 21$。
阅读全文
posted @ 2020-04-26 18:40
George1123
阅读(170)
评论(0)
推荐(2)
浙公网安备 33010602011771号