已知两点坐标,计算汽车行驶的方向【转】
转自http://www.cnblogs.com/xuanfeng/archive/2010/04/22/1718074.html
1. 场景:已知汽车行驶过程中的2个GPS坐标点A(n1,e1),B(e),计算它行驶的方向。
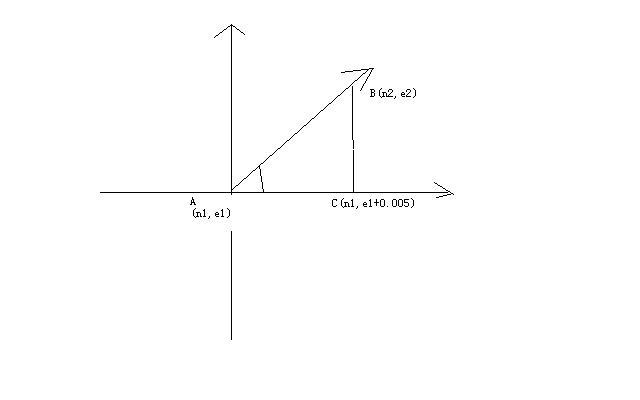
2. 分析:如上图所示,知道了两个点A、B,可以假设一个C点,让三个点构成一个直角三角形。现在可以知道,A,B,C三点的GPS坐标就很容易求出三个角的对边长度a,b,c(参考计算两个GPS坐标的距离)。根据余弦定下CosB=(a2+c2-b2)/
3.C#实现代码。
 计算汽车行驶的方向
计算汽车行驶的方向
/// <summary>
///计算两点GPS坐标的距离
/// </summary>
/// <param name="n1">第一点的纬度坐标</param>
/// <param name="e1">第一点的经度坐标</param>
/// <param name="n2">第二点的纬度坐标</param>
/// <param name="e2">第二点的经度坐标</param>
/// <returns></returns>
public static double Distance(double n1, double e1, double n2, double e2)
{
double jl_jd = 102834.74258026089786013677476285;
double jl_wd = 111712.69150641055729984301412873;
double b = Math.Abs((e1 - e2) * jl_jd);
double a = Math.Abs((n1 - n2) * jl_wd);
return Math.Sqrt((a * a + b * b));
}
/// <summary>
/// 已知汽车行驶的两个GPS点,求汽车行驶的方向
/// </summary>
/// <param name="n1">第一个GPS点纬度</param>
/// <param name="e1">第一个GPS点经度</param>
/// <param name="n2">第二个GPS点纬度</param>
/// <param name="e2">第二个GPS点经度</param>
/// <returns></returns>
public static double GetBusDirection( double n1,double e1, double n2, double e2)
{
double e3 = 0;
double n3 = 0;
e3 = e1 + 0.005;
n3 = n1;
double a = 0;
double b = 0;
double c = 0;
a = Distance(e1, n1, e3, n3);
b = Distance(e3, n3, e2, n2);
c = Distance(e1, n1, e2, n2);
double cosB = 0;
if ((a * c) != 0)
{
cosB = (a * a + c * c - b * b) / (2 * a * c);
}
double B = Math.Acos(cosB) * 180 / Math.PI;
if(n2<n1)
{
B=180+(180-B);
}
return B;
}
///计算两点GPS坐标的距离
/// </summary>
/// <param name="n1">第一点的纬度坐标</param>
/// <param name="e1">第一点的经度坐标</param>
/// <param name="n2">第二点的纬度坐标</param>
/// <param name="e2">第二点的经度坐标</param>
/// <returns></returns>
public static double Distance(double n1, double e1, double n2, double e2)
{
double jl_jd = 102834.74258026089786013677476285;
double jl_wd = 111712.69150641055729984301412873;
double b = Math.Abs((e1 - e2) * jl_jd);
double a = Math.Abs((n1 - n2) * jl_wd);
return Math.Sqrt((a * a + b * b));
}
/// <summary>
/// 已知汽车行驶的两个GPS点,求汽车行驶的方向
/// </summary>
/// <param name="n1">第一个GPS点纬度</param>
/// <param name="e1">第一个GPS点经度</param>
/// <param name="n2">第二个GPS点纬度</param>
/// <param name="e2">第二个GPS点经度</param>
/// <returns></returns>
public static double GetBusDirection( double n1,double e1, double n2, double e2)
{
double e3 = 0;
double n3 = 0;
e3 = e1 + 0.005;
n3 = n1;
double a = 0;
double b = 0;
double c = 0;
a = Distance(e1, n1, e3, n3);
b = Distance(e3, n3, e2, n2);
c = Distance(e1, n1, e2, n2);
double cosB = 0;
if ((a * c) != 0)
{
cosB = (a * a + c * c - b * b) / (2 * a * c);
}
double B = Math.Acos(cosB) * 180 / Math.PI;
if(n2<n1)
{
B=180+(180-B);
}
return B;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号