DS博客作业--07查找
1.本周学习总结(0--2分)
1.思维导图
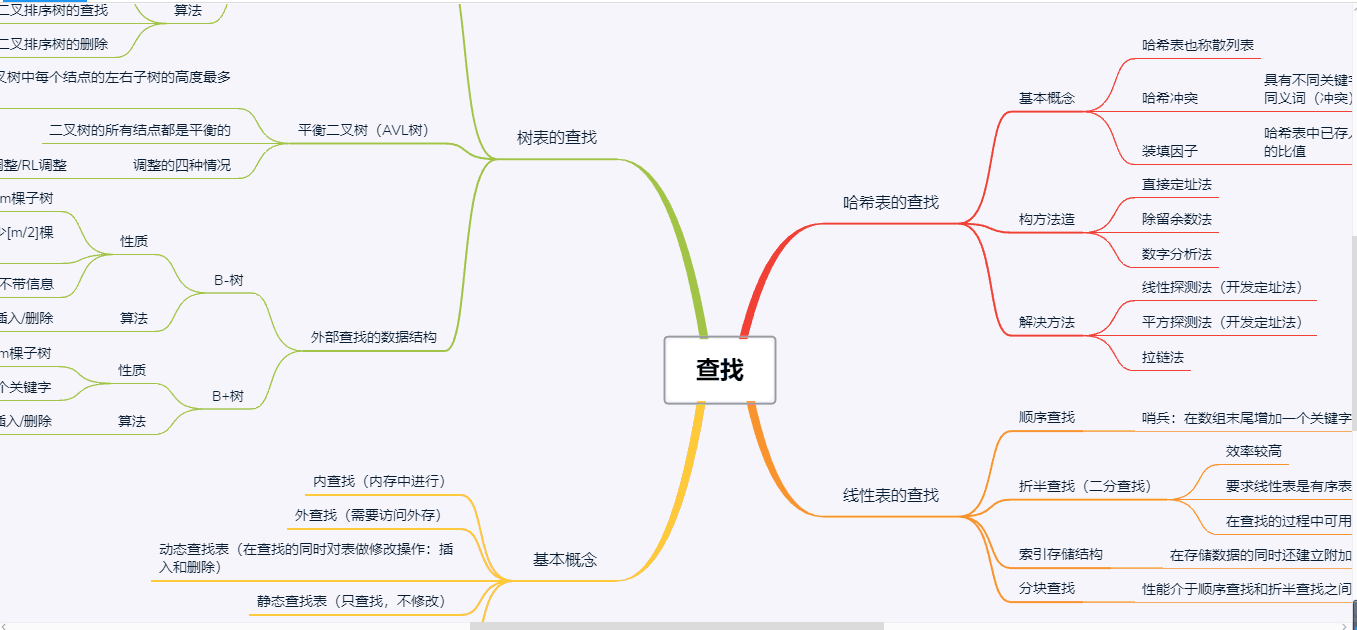
2.谈谈你对查找运算的认识及学习体会。
查找一章所学习的算法方法比较多,刚开始做课堂派时理解了,但现在上完后,各种算法放在一起就会混乱,然后就不懂,就得翻书看看了。还有就是关于它的算法我理解了之后吧,不看书写代码又写不出来。但是我觉得这章画图之类的挺好玩的。不过在画图还是需要仔细小心,会容易出错。
2.PTA实验作业(6分)
本周要求挑3道题目写设计思路、调试过程。设计思路用伪代码描述。题目选做要求:
原则上题目选择越难,代码量越大分值越高。
2.1.题目1:6-1 二叉搜索树的操作集 (30 分)
本题要求实现给定二叉搜索树的5种常用操作。
函数接口定义:
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
函数Insert将X插入二叉搜索树BST并返回结果树的根结点指针;
函数Delete将X从二叉搜索树BST中删除,并返回结果树的根结点指针;如果X不在树中,则打印一行Not Found并返回原树的根结点指针;
函数Find在二叉搜索树BST中找到X,返回该结点的指针;如果找不到则返回空指针;
函数FindMin返回二叉搜索树BST中最小元结点的指针;
函数FindMax返回二叉搜索树BST中最大元结点的指针。
2.1.1设计思路(伪代码)
伪代码尽量文字描述,请用下面markdown符号渲染。如:
定义变量i表示XXXXX
for i=0 to n-1
a[i]执行运算等等。
end for
** 设计思路、伪代码要用```符号渲染 **
BinTree Insert( BinTree BST, ElementType X )
{
if(BST==NULL) //判断树是否空;
{
BST= (BinTree )malloc(sizeof (BinTree)); //若树空,创建一个新结点,且树根为X,左右孩子为空;
}
else if(X<BST->Data) //X小于根结点;
{
//递归,在左子树中找插入位置;
}
else //X大于根结点;
{
//递归,在右子树中找插入位置;
}
return BST; //返回根结点;
}
BinTree Delete( BinTree BST, ElementType X )
{
if(BST==NULL) //空树删除失败,输出Not Found;
{
printf("Not Found\n");
return 0;
}
else
{
if(X==BST->Data ) //找到要删除的结点;
{
BinTree p; //申请新结点;
if(BST->Right ==NULL) //该树只有左孩子,无右孩子;
{
p=BST; //把树赋给p;
BST=BST->Left ; //把树的左孩子赋给树;
free(p); //释放(删除)根结点;
}
else if(BST->Left ==NULL) //该树只有右孩子,无左孩子;
{
//把树赋给p;
//把树的右孩子赋给树;
//释放(删除)根结点;
}
else //该有左右孩子;
{
BinTree r; //申请新结点;
r= FindMax(BST->Left); //调用FindMax()函数,找出左子树中最大结点数,并赋给r;
BST->Data = r->Data; //把树r的根赋给BST;
BST->Left = Delete(BST->Left, r->Data); //调用删除函数Delete();
}
return BST; //返回树结点;
}
else if(X<BST->Data ) //X比树根结点小;
{
BST->Left = Delete(BST->Left ,X); //递归在左子树中删除为X的结点;
}
else
{
//递归在右子树中删除为X的结点;
}
}
}
Position Find( BinTree BST, ElementType X )
{
if(BST==NULL||BST->Data ==X) //树BST空或找到X;返回BST;
{
return BST;
}
if(X<BST->Data ) //X比根结点小;
{
return Find(BST->Left ,X); //在左子树中递归查找;
}
else
{
//在左子树中递归查找;
}
}
Position FindMin( BinTree BST )
{
if(BST!=NULL) //判断树是否空;
{
while(BST->Left !=NULL) //最小结点在根结点的最左下结点;
{
BST=BST->Left ; //把树的左子树赋给树BST;
}
}
return BST; //返回BST;
}
Position FindMax( BinTree BST )
{
if(BST!=NULL) //判断树是否空;
{
while(BST->Right !=NULL) //最大结点在根结点的最右下结点;
{
}
}
return BST; //返回BST;
}
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)



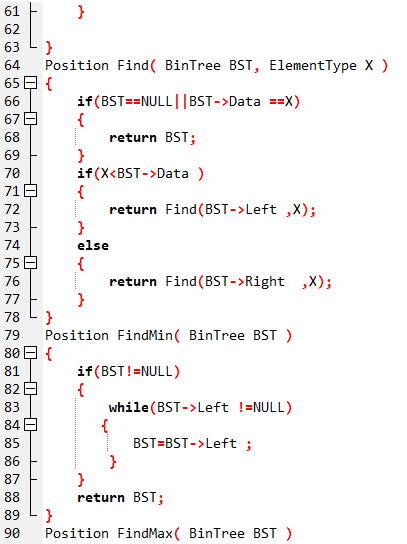

2.1.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:编译错误
- A1:应该把Delete()函数的最后弄成递归口,而不应该直接return.
- Q2:答案错误
- A2:在查找最大最小时的树的变化,比根大在右子树,比根小在左子树。
2.2 题目2:6-2 是否二叉搜索树 (25 分)
函数IsBST须判断给定的T是否二叉搜索树,即满足如下定义的二叉树:
定义:一个二叉搜索树是一棵二叉树,它可以为空。如果不为空,它将满足以下性质:
非空左子树的所有键值小于其根结点的键值。
非空右子树的所有键值大于其根结点的键值。
左、右子树都是二叉搜索树。
如果T是二叉搜索树,则函数返回true,否则返回false。
2.2.1设计思路(伪代码)
int a[100]; 定义一个数组a和i并初值为0;
int i = 0;
bool IsBST()
{
if(树是否空)
{
调用IsBST()函数,用左子树递归;
把树根结点的值赋给数组a;
调用IsBST()函数,用右子树递归;
}
for( 一层循环)
{
if(比较a[j-1]和 a[j]的大小关系)
{
如果a[j-1]大于等于a[j],返回false;
}
}
返回true;
}
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)

2.2.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:编译错误。
- A1:在if判断树是否空里面对左子树和右子树的语法使用的不清晰,增加了没有必要的语句。
2.3 题目3:6-3 二叉搜索树中的最近公共祖先 (25 分)
在一棵树T中两个结点u和v的最近公共祖先(LCA),是树中以u和v为其后代的深度最大的那个结点。现给定某二叉搜索树(BST)中任意两个结点,要求你找出它们的最近公共祖先。
函数接口定义:
int LCA( Tree T, int u, int v );
其中Tree的定义如下:
typedef struct TreeNode *Tree;
struct TreeNode {
int Key;
Tree Left;
Tree Right;
};
函数LCA须返回树T中两个结点u和v的最近公共祖先结点的键值。若u或v不在树中,则应返回ERROR。
2.3.1设计思路(伪代码)
int FindKey( )
{
if(树空)
返回ERROR;
if(T->Key等于u)
{
返回1;
}
if(T->Key大于u)
{
返回FindKey(T->Left, u ) ,在左子树中找;
}
else(T->Key小于u)
{
返回FindKey(T->Right, u ) ,在右子树中找;
}
}
int LCA( )
{
if(树空)
返回ERROR;
if(FindKey( T, u)&&FindKey( T, v)) //调用FindKey( )函数;
{
if(T->Key大于u和T->Key小于v或T->Key大于v&&T->Key小于u)
返回 T->Key;
else if(T->Key等于u或T->Key等于v)
返回 T->Key;
else if(T->Key大于u或T->Key大于v)
返回 LCA( T->Left, u, v ); //调用LCA()函数,用左子树,u,v做参数;
else
return LCA( T->Right, u, v ); //调用LCA()函数,用右子树,u,v做参数;
}
else
{
返回 ERROR;
}
}
2.3.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
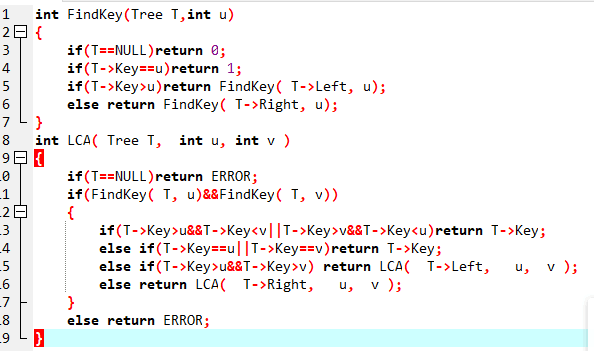
2.3.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:答案错误
- A1:在比较时,各种情况考虑不周全,缺少一种情况运行都是错误的。
- Q2:部分正确
- A2:T-key在和u,v比较时,比较的条件设的不理想,因为情况很多,不够仔细,条件就错误了。
3、阅读代码(-2--2分)
找一份和查找运算相关代码,谈谈你对这个代码认识体会。
考研题种关于查找、二叉搜索树内容。
ACM、PTA天梯赛、leecode面试刷题网站,找查找相关题目阅读分析。
请按照下面内容填写代码阅读内容。请未必认真完成,如果发现应付,没有介绍代码思路、体会等扣分。
3.1 题目:二叉树展开为链
- 介绍代码解决问题
给定一个二叉树,原地将它展开为链表。
例如,给定二叉树
1
/ \
2 5
/ \ \
3 4 6
将其展开为:
1
\
2
\
3
\
4
\
5
\
6
3.2 解题思路
运用后序遍历和递归方法,递归返回值为当前节点的最后一个节点,然后再把返回的最后一个节点指向当前的右节点,当前的右节点指向左节点,置空左节点即可。 需特别注意没有处理空root的情况,所以进入函数时需要if(!root) return; recursive(root);
3.3 代码截图
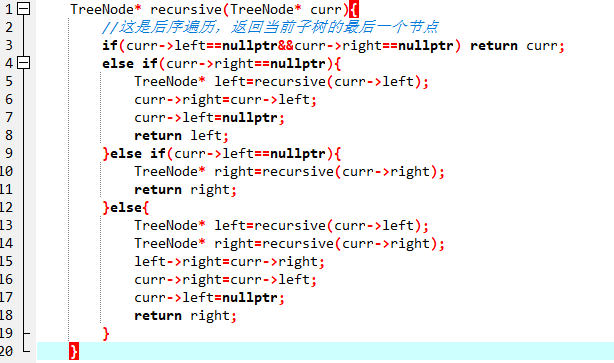
3.4 学习体会
NULL在C和C++中不等价,在C中习惯将NULL定义为void *指针值0,也可以定义为整型常数0。但在C++中,NULL被明确定义为整型常数0.如果C++还是使用使用void *的隐形式类型转换,则可能会带来语义二义性问题。nullptr初始化对象,能避免0指针的二义性问题。注意不能将nullptr赋给整型。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号