数三角形

题面

给定一个$n*m$的网格，请计算三点都在格点上的三角形共有多少个。下图为$4*4$的网格上的一个三角形。

 

 

 

 

 

 

 

 

 

 

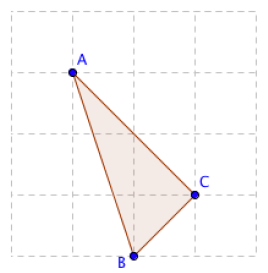
注意：三角形的三点不能共线。

思路

三角形总数=随便在点阵上选3个点的方案数-共线方案数

总方案数

设t为总点数，为$(n+1)*(m+1)$，看看图就知道了。

随便选3个点的方案数$\frac{t!}{(t-3)!3!}=\frac{(t-2)\ast(t-1)\ast t}6$

横竖不合法方案

设$calc(x)=\frac{x!}{(x-3)!3!}=\frac{(x-2)\ast(x-1)\ast x}6$

横行为$calc(m+1)*(n+1)$

竖列为$calc(m+1)*(n+1)$

斜线不合法方案

斜线整点(除端点)公式为$gcd(x_1-x_2,y_1-y_2)-1$

前提是$x_1>x_2,y_1>y_2,两点为端点$

然后就是考虑优化了

1. 显然在点阵中相同斜线可以不用计算，平移即可
2. 对称斜线乘2即可，也就是说只用考虑单向的斜线

 

 

 

 

 

 

 

 

 

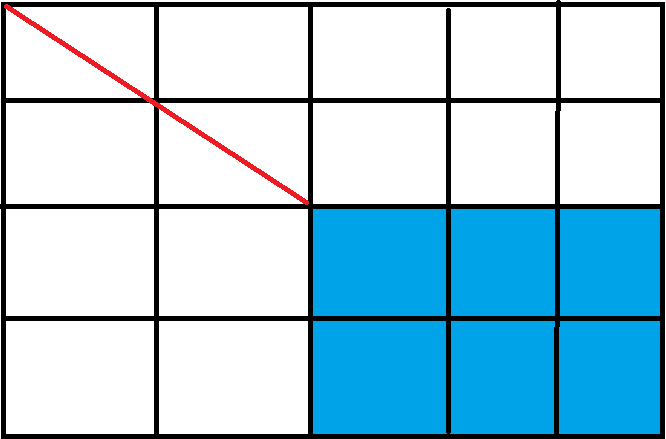
如图斜线，蓝色部分的点都是该斜线下面那个端点(2,2)可以移到的(边缘也可以)，如果不是则上面的端点(0,0)会超出点阵，所以每个端点的平移方案有$(n-i+1)*(m-j+1)$。

则可枚举右下端点坐标。

把所有的$(n-i+1)*(m-j+1)*2*(gcd(i,j)-1)$相加即可。

代码

#include<bits/stdc++.h>
using namespace std;
long long n,m;
long long calc(long long x){return x*(x-1)*(x-2)/6;}
int main()
{
    scanf("%lld%lld",&n,&m);
    long long t=(n+1)*(m+1);
    long long tot=t*(t-1)*(t-2)/6-calc(n+1)*(m+1)-calc(m+1)*(n+1);
    for (int i=1;i<=n;i++)
     for (int j=1;j<=m;j++)
      tot-=(n-i+1)*(m-j+1)*2*(__gcd(i,j)-1);
    cout<<tot<<endl;
    return 0;
}