缺一分治 & CF1425B Blue and Red of Our Faculty! 笔记

这是一种 01 背包，但是每次强制第 \(i\) 个物体不选，然后询问背包，暴力做是 \(O(n^2V)\) 的。

考虑分治，当递归到区间 \([l,r]\) 时，不将 \([l,r]\) 放入背包，递归时就是 \([l,\mathrm{mid}]\) 放入背包然后递归 \((\mathrm{mid},r]\)，反过来同理，当递归到叶子节点时结束，分治树的层数是 \(O(\log n)\) 层，每层每个物品只会放入 / 移出背包 \(O(1)\) 次，因此时间复杂度 \(O(nV\log n)\)。

题解

首先要看清题，这个图是若干个包含 \(1\) 的环构成的。

考虑遍历完后，树上的环有哪些情况。

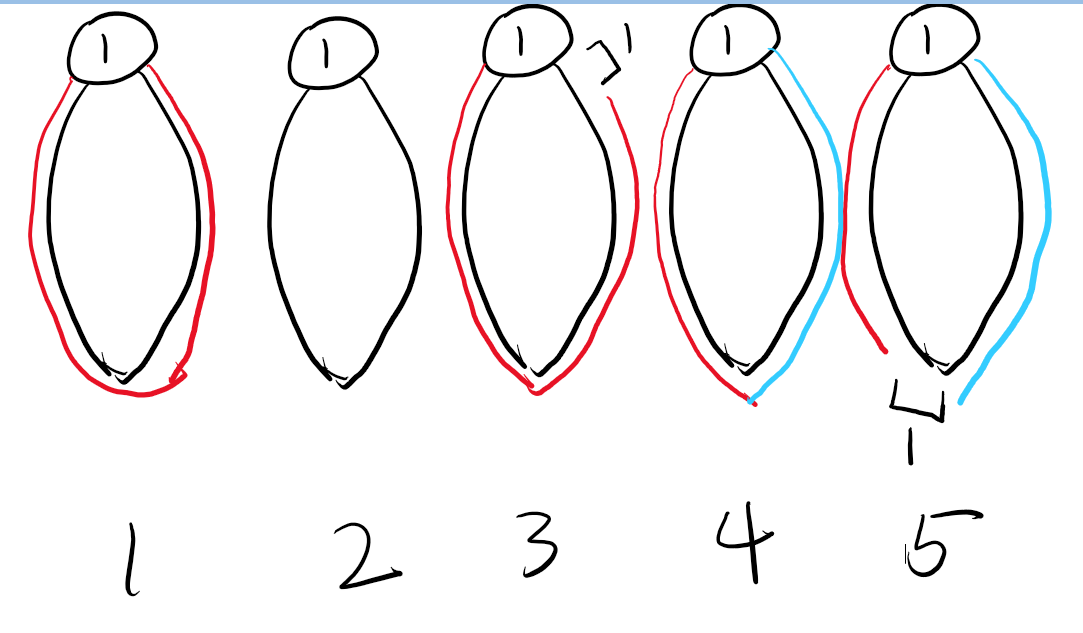
不难发现：

• 环 \(3,4,5\) 作为终止状态，三种环总共只会在一个方案中出现至多一次。
• 环 \(3\) 与环 \(5\) 的这个接口长度必然是 \(1\)，不然还能走。
• 环 \(3\) 出现说明其他所有环都是环 \(1\)，即不存在环 \(2\)。
• 若环 \(3,4,5\) 均不出现，则环 \(2\) 不出现。

可以发现，只有环 \(1,2,3\) 的情况只要随便 DP 一下就好了。先考虑以环 \(4,5\) 为终止状态的部分，由于我们不关心到底有几条红边和蓝边，于是套路地状态只记录边数差值即可，即设 \(f_{i,j}\) 表示考虑前 \(i\) 个环均为环 \(1,2\)，边数差为 \(j\) 的方案数，转移很简单，环 \(1\) 红边 / 环 \(1\) 蓝边 / 不选三种，\(a_i\) 为环长。

\[f_{i,j}\gets f_{i-1,j-a_i}+f_{i-1,j+a_i}+f_{i-1,j} \]

其中第一维其实可以直接滚掉。考虑确定环 \(4,5\) 是哪个环，那么就变成了缺一分治模板。

当我们递归到 \(l=r\) 时，这个位置就是 \(4,5\) 对应的环，我们枚举蓝边的个数 \(x\)，即可求出红边的个数 \(a_l-x\)（环 \(4\)），于是答案就是 \(2\times f_{l,a_i-x-x}\)。环 \(5\) 同理，但是要注意不要和环 \(3\) 重复了。

接着考虑只有环 \(1,2,3\) 的情况，设 \(f_{i,j,0/1}\) 表示前 \(i\) 个环红蓝边差距为 \(j\)，有多少个环 \(3\)，其他环都是环 \(1\) 的方案数。

\[f_{i,j,k}\gets f_{i-1,j-a_i,k}+f_{i-1,j+a_i,k} \]

\[f_{i,j,1}\gets f_{i-1,j-(a_i-1),0}+f_{i-1,j+(a_i-1),0} \]

由于这里没有讨论接入方式（显然环 \(3\) 有两种接入方式），因此最终答案要 \(f_{n,0,1}\times 2\)。

时间复杂度 \(O(m^2\log m)\)，空间复杂度 \(O(m^2)\)。