hdu 1693 Eat the Trees
Eat the Trees
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2052 Accepted Submission(s): 998
Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
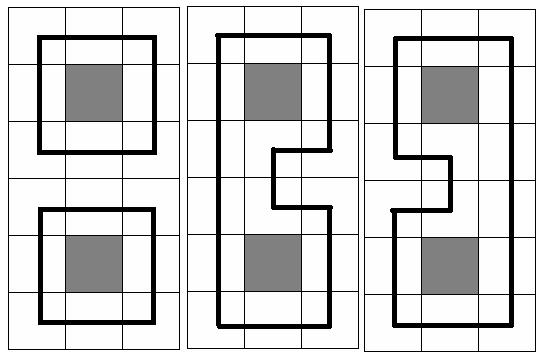
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.
Sample Input
2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1
Sample Output
Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.
Source
2008 “Sunline Cup” National Invitational Contest
Recommend
wangye
参考:http://hi.baidu.com/fqq11679/item/dc4948e3edb9963c87d9ded9

如上图,我们用F[i,j,k]表示轮廓线在i行j列出外凸,轮廓线状态为k的方案数。
这里k是一个c+1位二进制数,1表示轮廓线第i个单元有插头,0表示没有。
那么转移就考虑两种,第一种是换行,这个就要把k先右移一位,然后把k
的前两位转移成凸起,更新F[i+1,1,k']。
第二种就是直接右推一格,这个就是直接在k中找出凹角对应的两位数,转换
得到新状态k'然后更新F[i,j+1,k']。
至于k如何转k'只需考虑凹角的几种情况:
1.凹角为11(横竖都有插头):新状态k'的这两位均为0,因为两个度用完了。
2.凹角为01(只有横边有插头):新状态k'可以是01或者10。
3.凹角为10(只有竖边有插头):同上。
4.凹角为00(都没插头):要么11,要么00。(00的条件是此格为障碍)
这样Dp一下,最后的答案就是F[r][c][0]。
1 //15MS 4844K 1649 B C++ 2 /* 3 4 第一题插头DP. 5 6 题意: 7 给出一个图,1表示有树,0 表示没有,没有树的不能通过 8 求多条回路把树吃完的方法数 9 10 插头DP: 11 dp[i][j][k]表示第i行j列轮廓线状态为k的方案数 12 13 1.凹角为11(横竖都有插头):新状态k'的这两位均为0,因为两个度用完了。 14 2.凹角为01(只有横边有插头):新状态k'可以是01或者10。 15 3.凹角为10(只有竖边有插头):同上。 16 4.凹角为00(都没插头):要么11,要么00。(00的条件是此格为障碍) 17 18 这样Dp一下,最后的答案就是dp[n][m][0]。 19 20 */ 21 #include<stdio.h> 22 #include<string.h> 23 __int64 dp[12][12][1<<12]; 24 int g[12][12]; 25 int main(void) 26 { 27 int t,n,m,k=1; 28 scanf("%d",&t); 29 while(t--) 30 { 31 scanf("%d%d",&n,&m); 32 for(int i=1;i<=n;i++) 33 for(int j=1;j<=m;j++) 34 scanf("%d",&g[i][j]); 35 memset(dp,0,sizeof(dp)); 36 dp[0][m][0]=1; 37 for(int i=1;i<=n;i++){ //枚举列 38 for(int j=0;j<(1<<m);j++) //*行间状态转移 39 dp[i][0][j<<1]=dp[i-1][m][j]; 40 for(int j=1;j<=m;j++){ //枚举行 41 int p=(1<<j); //第j个轮廓段(上) 42 int q=(1<<(j-1)); //第j-1个轮廓段(左) 43 for(int k=0;k<(1<<(m+1));k++){ //枚举全部状态 44 if(g[i][j]){ //有树 45 if(!(k&p) && !(k&q)) //没相交00 46 dp[i][j][k]=dp[i][j-1][k+p+q]; 47 else if((k&p) && (k&q)) //两相交11 48 dp[i][j][k]=dp[i][j-1][k-p-q]; 49 else{ //一相交 01 or 10 50 dp[i][j][k]+=dp[i][j-1][k]; 51 dp[i][j][k]+=dp[i][j-1][k^p^q]; 52 } 53 }else{ //没树 54 if(!(k&p) && !(k&q)) 55 dp[i][j][k]=dp[i][j-1][k]; 56 else dp[i][j][k]=0; 57 } 58 //printf("dp[%d][%d][%d]=%d\n",i,j,k,dp[i][j][k]); 59 } 60 } 61 } 62 printf("Case %d: There are %I64d ways to eat the trees.\n",k++,dp[n][m][0]); 63 } 64 return 0; 65 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号