research2

符号配对

一、实现功能描述

括号运算是表达式运算中的一个重要部分，不考虑具体运算仅指括号的正确匹配时，具有如下特征：
（1）它必须成对出现，如“(”“)”是一对，“[”与“]”是一对；
（2）出现时有严格的左右关系；
（3）可以以嵌套的方式同时出现多组多括号，但必须是包含式嵌套，不允许交叉式嵌套。比如“( )”、“[([][])]”这样是正确的，“[(])”或“([()))”或 “(()]”是不正确的。
（4）将处理的括号扩展为针对“()”“[]”“{}”三类。

1. 设计栈数据结构用于存储待匹配括号
2. 实现括号匹配的核心算法：
   • 左括号入栈
   • 判断右括号与栈顶元素匹配？
3. 支持三种括号类型：(), [], {}
4. 检测嵌套合法性，禁止交叉嵌套

二、方案比较与选择

方案对比：

对比维度	数组栈	链栈	优选
访问效率	✅ O(1)连续随机访问，缓存友好	❌ 指针跳转访问，缓存不友好	数组（频繁访问栈顶）
内存占用	⚠️ 固定预分配，可能有浪费	✅ 动态分配，按需使用内存	平手（嵌套深度通常有限）
内存碎片	✅ 无碎片	❌ 频繁分配释放可能产生碎片	数组
操作复杂度	✅进出栈仅需2步操作	❌ 每个操作需4步+内存分配	数组
扩容灵活性	❌ 需重新分配内存复制数据	✅ 天然支持动态扩展	链表（但此问题通常不需要）
代码简洁性	✅ 无需处理指针和动态内存	❌ 需管理节点内存和指针	数组

选择方案 数组栈 的原因：

括号匹配问题往往嵌套深度可控，无需动态扩展，且要高频操作栈顶~

三、设计算法描述

1. 算法思想示例

"([{}])"

当前字符	操作类型	栈内状态（栈底→栈顶）	动作说明
(	入栈	[ '(' ]	左括号直接入栈
[	入栈	[ '(' , '[' ]	新的左括号入栈
{	入栈	[ '(' , '[' , '{' ]	继续入栈
}	匹配出栈	[ '(' , '[' ]	}与栈顶{匹配，弹出{
]	匹配出栈	[ '(' ]	]与栈顶[匹配，弹出[
)	匹配出栈	[]（空栈）	)与栈顶(匹配，弹出(

最终结果：栈为空且都匹配 → 匹配成功

2. 关键算法流程图

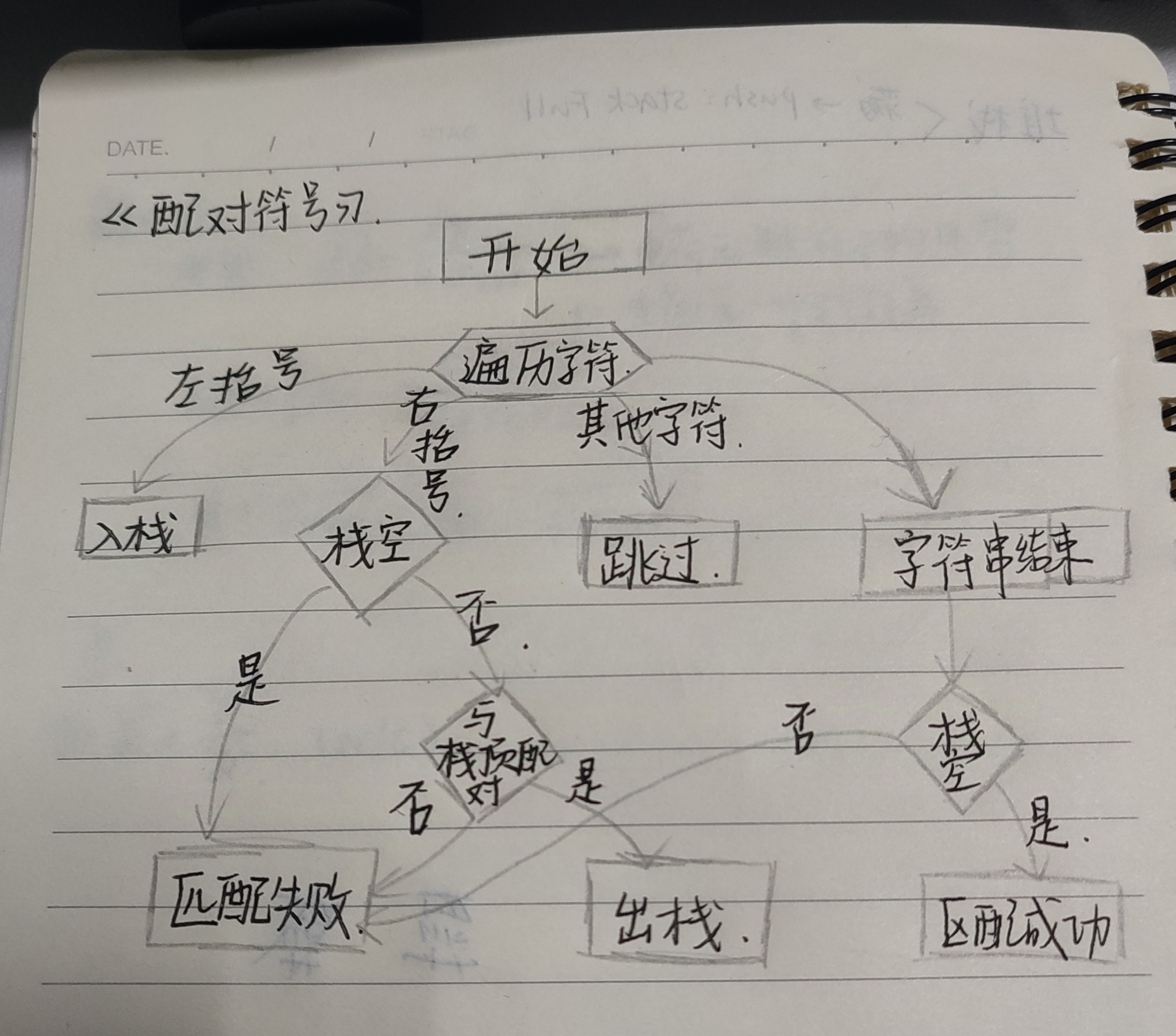
四、算法实现

#include <stdio.h>
#include <string.h>
int main() {
    int top, i, j, flag;
    char stack[500];//栈顶，储存左符号
    char tmp[500];//暂时储存六个目标符号
    char str[500];//输入的所有字符
    j = 0;//当作tmp下标，顺便记录目标符号的个数
	top = 0;//0_base
	flag = 1;//默认匹配
	//输入
    while (gets(str)) {
        if (str[0] == '?') break;//输入英文?，结束输入，其余情况下保存到str数组里
        for (i = 0; i < strlen(str); i++) {
            if (str[i] == '(' || str[i] == '{' || str[i] == '[' || 
                str[i] == ')' || str[i] == '}' || str[i] == ']') {
                tmp[j++] = str[i];//暂时储存六个目标符号
            } 
        }
    }

    for (i = 0; i < j; i++) {//这里的j是全局变量，就是目标符号的个数，用i遍历所有目标
        if (tmp[i] == '(' || tmp[i] == '{' || tmp[i] == '[') {
            stack[top++] = tmp[i];//记录栈顶符号（左符号）
        }
    //碰到右符号时，栈不空且为对应匹配的左符号，就把左符号出栈，否则是错误的配对
        if (tmp[i] == ')') {
            if (top > 0 && stack[top-1] == '(') {//0_base
                top--;//出栈
            } else {
                flag = 0;//出错了
                break;//直接跳出循环
            }
        }
        if (tmp[i] == '}') {
            if (top > 0 && stack[top-1] == '{') {
                top--;
            } else {
                flag = 0;
                break;
            }
        }
        if (tmp[i] == ']') {
            if (top > 0 && stack[top-1] == '[') {
                top--;
            } else {
                flag = 0;
                break;
            }
        }
    }

    if (flag && top == 0) {//栈空且与栈顶匹配，证明成功了
        printf("Successful pairing!\n");
    } else {
        printf("Something wrong\n");
    }

    return 0;
}

五、实验测试结果与分析

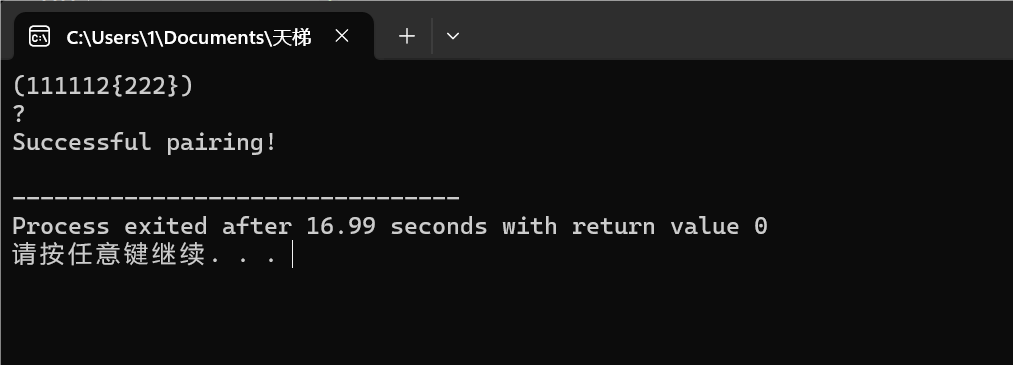
图1-1

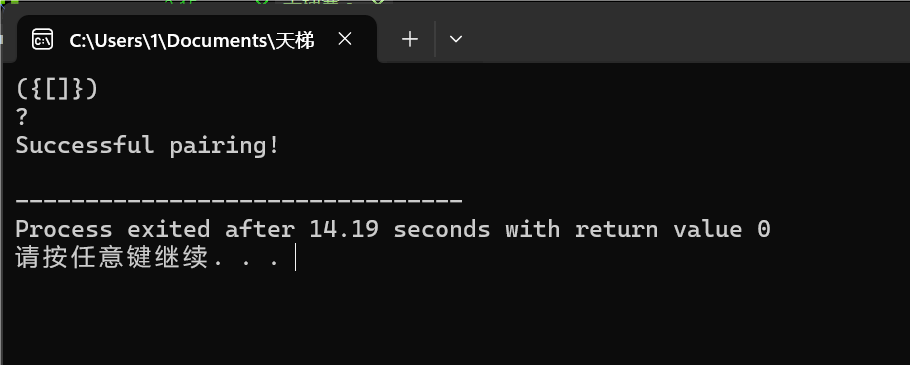
图1-2

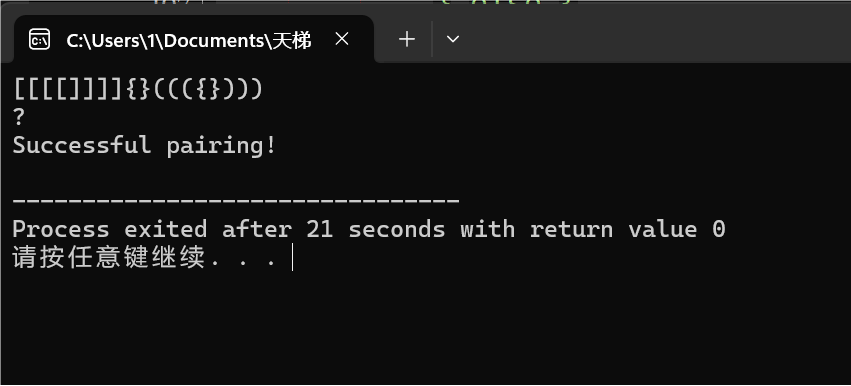
图1-3
图1-1，1-2，1-3为成功配对测试案例

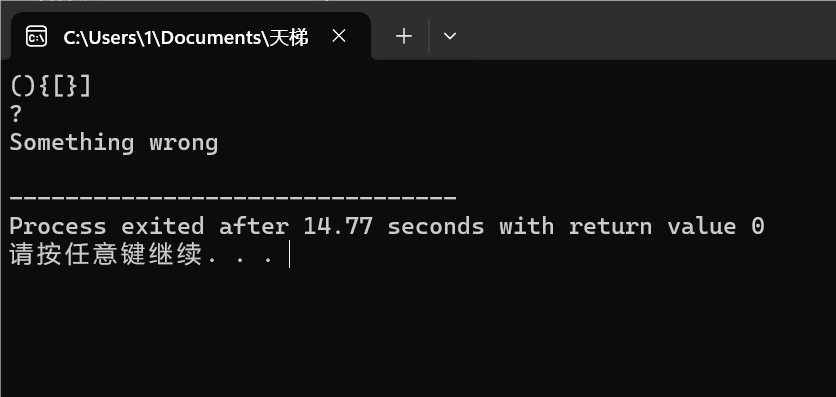
图1-4：交叉式嵌套❌

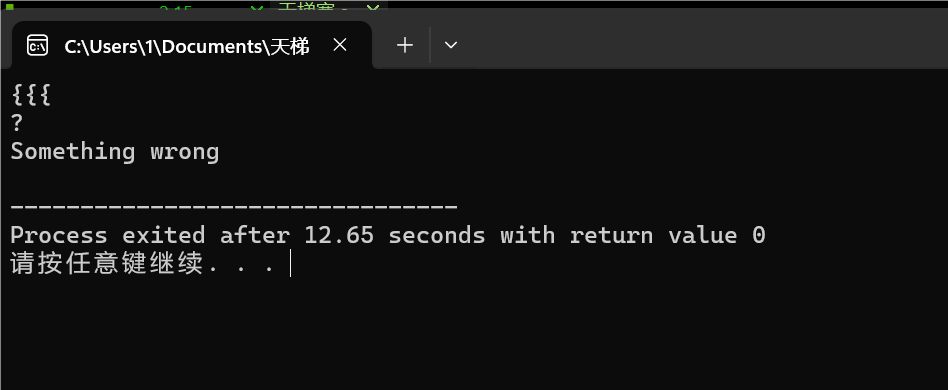
图1-5：左右关系❌

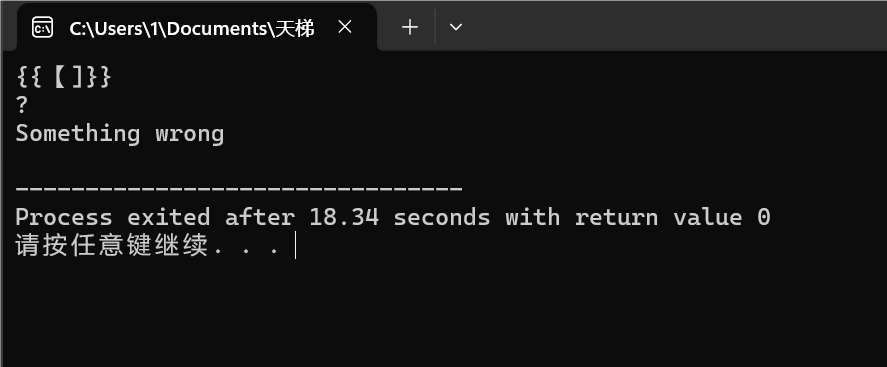
图1-6：中文输入的【不存在与目标符号中*

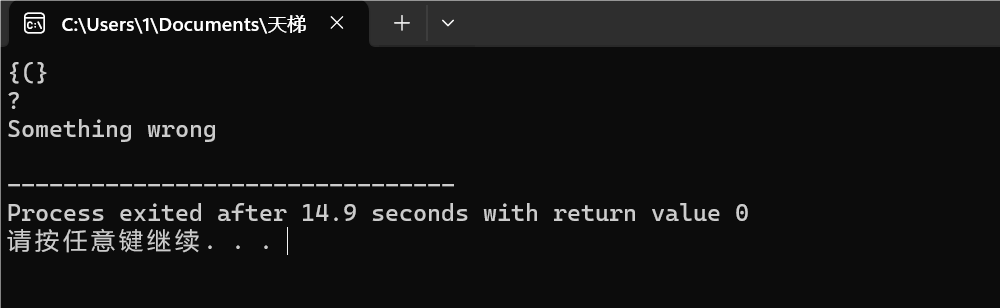
图1-7：未成对出现❌

1. 时间复杂度：O(n)
   • 单次遍历字符串，每个字符处理时间为O(1)
2. 空间复杂度：O(n)
   • 最坏情况下所有字符都是左括号
3. 优化方向：
   • 动态扩容栈空间
   • 提前终止检测（j为偶数必然不匹配）

六、思考及学习心得

通过本次实验，我深入理解了栈结构"后进先出"特性在括号匹配问题中的运用以及如何权衡数组栈和链栈的usage。在实现过程中遇到并解决了以下问题：

1. 边界条件处理：最初未考虑纯左括号字符串（((( )的情况，通过增加最终栈空检查完善了逻辑。测试案例[的失败让我意识到必须同时满足两个条件：（1）所有右括号都能匹配（2）最终没有剩余左括号。
2. 类型扩展实践：从单一括号类型扩展到三种类型时，发现简单的计数器无法区分[]和()，改用栈结构后通过存储具体括号字符完美解决了类型匹配问题。
3. 嵌套规则验证：通过分析[(])这类交叉嵌套案例，理解了栈结构如何天然阻止非法嵌套——只有当栈顶元素与当前右括号严格匹配时才允许出栈，否则立即终止。
   与递归解法相比，栈实现的迭代算法空间效率更高（递归深度可能达到O(n)）。
4. 严谨的编程习惯：英文输入?，程序才终止，之前测试输的中文问号，一直没停止，还以为代码没写对！以后写文档，写代码都要额外关注输入法，“细节决定成败”。

简易行编辑

一、实现功能描述

编程实现一个简单的行编辑功能：用户可以输入一行内容，并可进行简易编辑，做到：
（1）遇到输入部分内容有误时操作退格符“#”表示前一位无效；
（2）“@”表示之前的内容均无效。
功能：

1. 设计基于栈的行编辑器数据结构
2. 实现以下编辑功能：
   • #：删除前一个字符
   • @：清空当前行
3. 支持常规字符输入
4. 实时显示编辑结果

二、方案比较与选择

方案对比：

比较项	数组栈	链表栈
代码难度	⭐（简单）	⭐⭐⭐（要管指针）
速度	⭐⭐⭐（飞快）	⭐⭐（慢）
内存	⭐⭐⭐（紧凑）	⭐（额外指针浪费空间）
适用场景	知道最大长度	长度不确定

选择方案 数组栈 的原因：

模拟编译器问题往往嵌套深度可控，无需动态扩展，数组栈又简单又快，题目没特殊要求时无脑选它！

三、设计算法描述

算法思想示例

核心逻辑

1. 初始化一个空栈（top = 0）
2. 逐个读取输入字符：
   • 普通字符（push，入栈）
   • # 退格（pop，删除栈顶）
   • @ 清空栈（top = 0）

最终栈内容即为编辑结果
按照数组顺序输出即可

2. 关键算法流程图

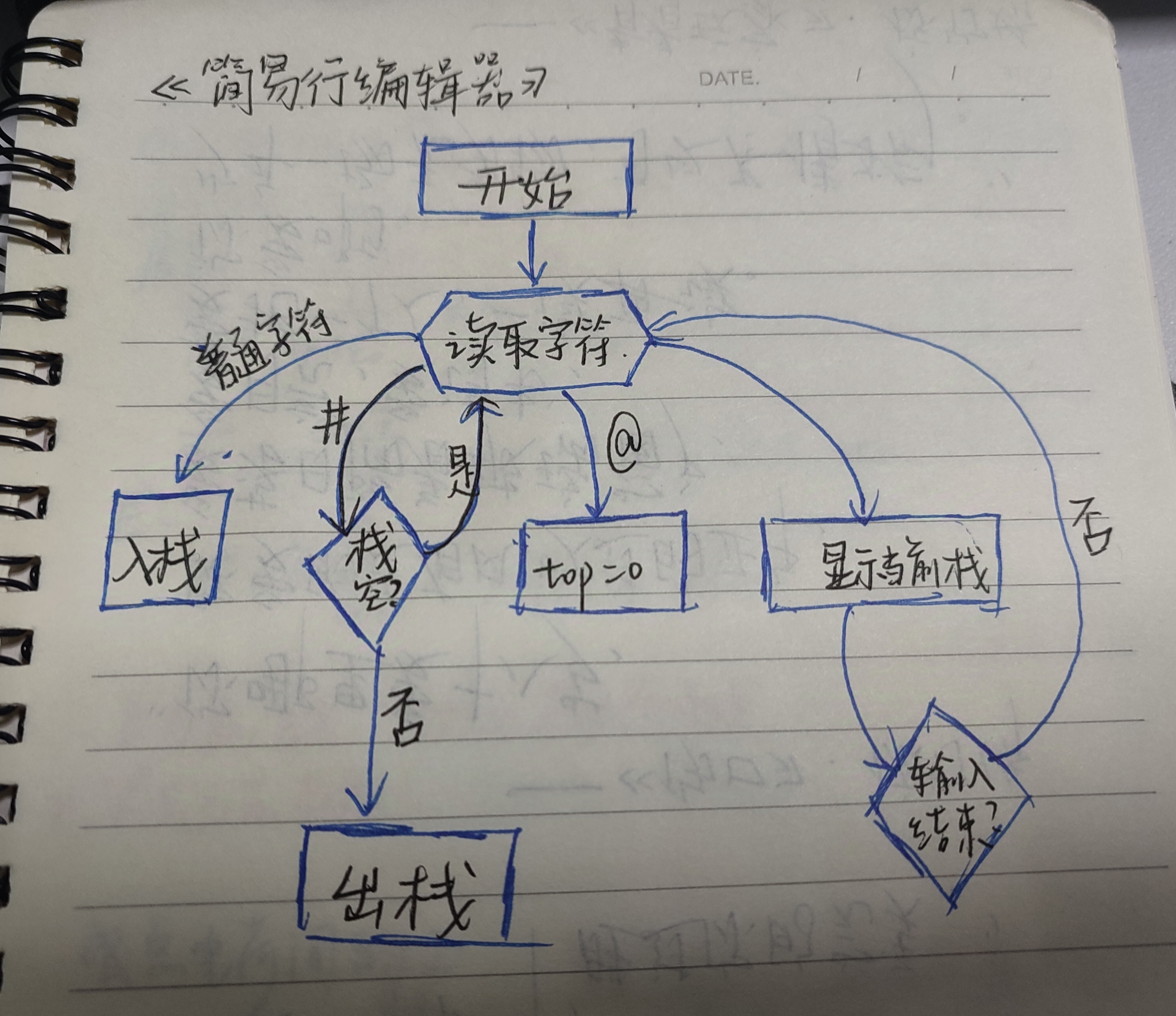
四、算法实现

#define MAX_LEN 1000
#include <stdio.h>
#include <string.h>
int main() {
    char stack[MAX_LEN];  //数组栈，储存经过处理（编辑过）的字符
    int top = 0;         // 栈顶指针（初始为空）
    char input[MAX_LEN]; //暂存输入的字符
    printf("please input ur content:\n");
    fgets(input, MAX_LEN, stdin);  // 输入字符串，直接读取
    for (int i = 0; input[i] != '\0' && input[i] != '\n'; i++) {
        // #相当于退格：如果栈不为空，删除前一个字符。
		if (input[i] == '#') {          
            if (top > 0) top--;//出栈 
        } 
        // @相当于清空行：reset栈顶
		else if (input[i] == '@') { 
            top = 0;
        } 
        // 普通字符：直接入栈
		else {          
            stack[top++] = input[i];
        }
    }

    // 输出
    printf("after text editing:");
    for (int i = 0; i < top; i++) {
        putchar(stack[i]);
    }
    printf("\n");

    return 0;
}

五、实验测试结果与分析

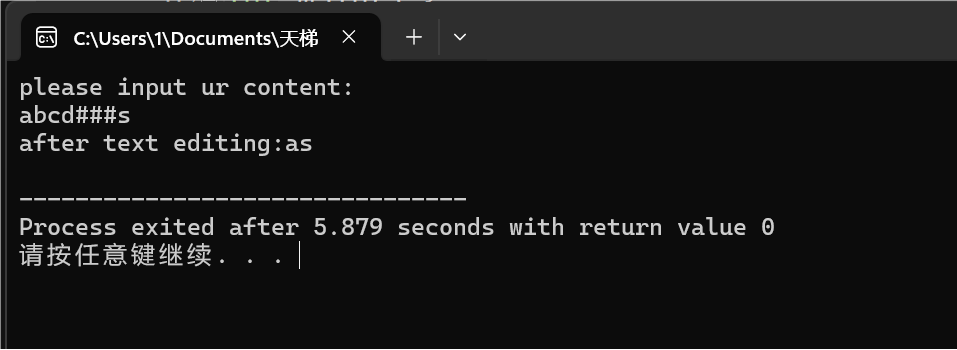
图：2-1正常退格

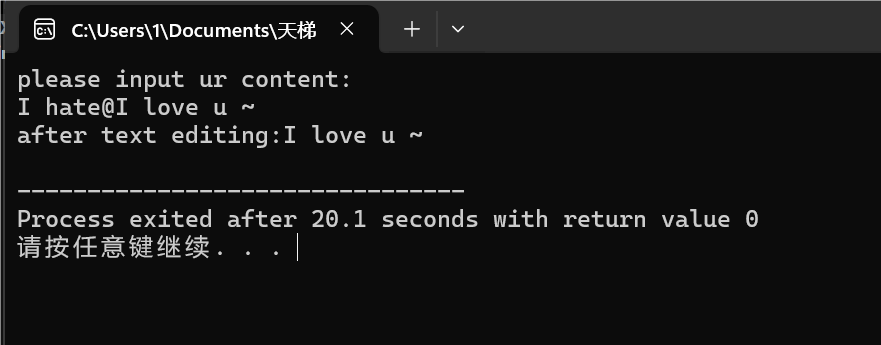
图：2-2正常清除

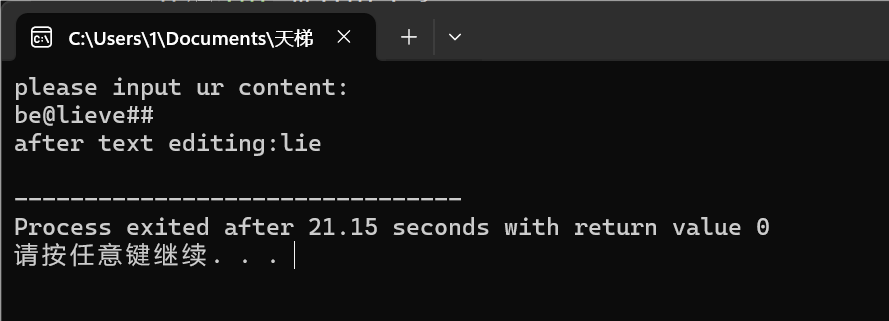
图：2-3正常清除与退格

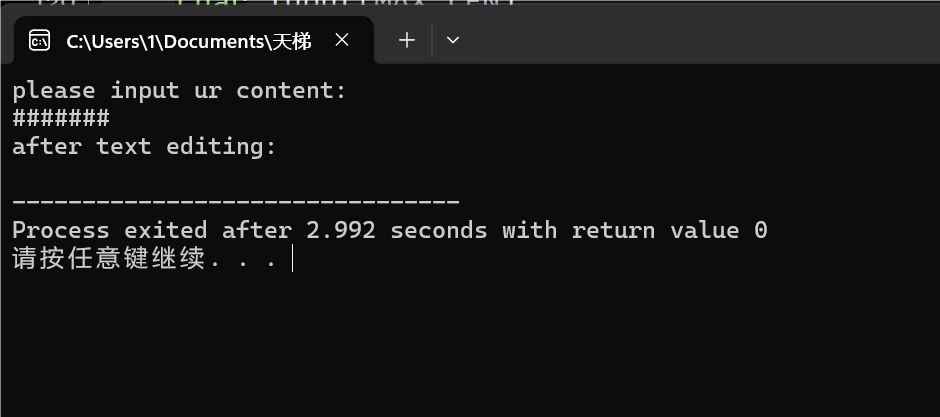
图：2-4只退格，内容为空

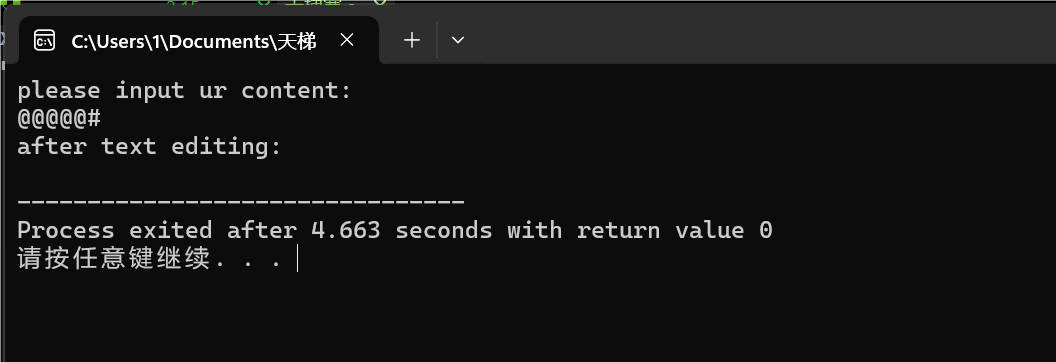
图：2-5只退格或清除，内容为空

六、思考及学习心得

1. 栈的运用：从理论到实际
刚开始学栈的时候，我只知道它是"先进后出"的，但做完这个实验才真正明白它有什么用。比如用户输入abc#，栈的pop操作刚好能删掉最后输入的字符，就像键盘的退格键一样方便。

• 对比测试：如果不用栈，直接用数组来操作，代码里会有一大堆if(pos>0) pos--这样的判断，很麻烦。用栈的话，只需要控制top指针就行了，代码更简单。
• 遇到的bug：有一次忘记检查栈是不是空的，导致top变成0后程序崩溃。后来加了if(top > 0)的判断就解决了。
• 学到的东西：栈不只是课本上的概念，它真的能解决实际问题——这里的退格功能。

2. 边界情况处理
刚开始写的程序有很多问题，特别是用户乱输入的时候：

• 问题1：用户输入一堆#####，top指针会变成负数，程序就崩溃了。解决办法：在删除字符前先检查栈是不是空的。
• 问题2：用户输入太长的内容，栈装不下。解决办法：设置一个最大长度，超过就报错。
• 总结：写程序不能只考虑正常情况，还要想到用户可能会乱输入，全方面考虑在开发中是很重要的！！

3. 可以改进的地方
虽然基本功能实现了，但还可以做得更好：

• 撤销功能：可以用两个栈，一个存当前内容，一个存历史记录，按Ctrl+Z就能撤销。
• 多行编辑：把现在的单行改成多行，用数组存每一行。
• 高亮显示：把#和@显示成不同颜色，看起来更清楚。
  这些功能现在还不会写，但我知道以后学了更多知识就能实现。
  总体说这个实验让我学会了：
  1.** 栈的实际应用**
  1. 要考虑各种奇怪的输入
  2. 调试程序要有耐心
  3. 一个小程序也可以不断改进
     虽然现在写的代码还很基础，但每次实验都能学到新东西，慢慢就能写出更厉害的程序了。

思考题

1. 对于这两个应用，除了用栈实现外，还可以用什么样的数据结构实现此功能?给出基本的方法描述。

1. 括号配对

• 递归+指针法
  p.s.适用于嵌套结构，但无法处理交叉嵌套 如 [(])
  描述：
  递归+指针法通过函数调用栈隐式存储状态，利用指针遍历字符串。
  • 当遇到左括号 ( 时，指针向前移动一位，然后递归调用函数处理嵌套部分。
  • 当遇到右括号 ) 时，返回 true，并更新指针到下一个字符。
  • 如果在遍历过程中无法找到匹配的括号，则返回 false。
• 双指针+计数器法
  适用于完全对称的括号结构（如 (())），但无法处理非对称情况（如 ()[]）
  描述：
  双指针+计数器法使用两个指针分别从字符串的两端向中间遍历，同时用一个计数器记录括号的匹配情况。
  • 左指针从左向右遍历，遇到左括号 ( 时计数器加 1，遇到右括号 ) 时计数器减 1。
  • 右指针从右向左遍历，遇到右括号 ) 时计数器加 1，遇到左括号 ( 时计数器减 1。
  • 如果计数器在任何时候变为负值，则说明括号不匹配，返回 false。
  • 最后检查计数器是否为 0，如果是则括号匹配，否则不匹配。

2. 行编辑器

• 数组
  描述：
  两个数组：一个存放原始输入内容，另一个存放编辑处理后的内容。遇见#退回索引，遇见@重置索引
• 双向链表
  遇见#删除前驱节点，遇见@清空链表

2.对于这两个应用，如果你对栈的基本操作（如压栈、出栈等）采用的是顺序栈（链式栈），那是否可以用链式栈（顺序栈）?谁更优?给出原因分析。

答：我采用的是数组栈。可以用链栈实现pop push，但是顺序栈更优，前面也有分析过为什么用顺序栈，还是再总结一下吧~
前提：这里的无论是括号配对问题还是编辑器模拟，嵌套的深度都有限，几乎不要求动态扩容。

• 书写代码上：数组栈的实现逻辑较为直观，代码简单；而链表栈需要处理指针操作，代码复杂度较高。
• 速度方面：数组栈由于数据在内存中连续存储，访问速度更快；链表栈则通过指针跳转：速度相对较慢。
• 内存使用上：数组栈更加紧凑，不产生内存碎片；而链表栈由于每个节点需要额外存储指针，会浪费空间。
• 可靠性：数组栈的固定大小特性可确保——无内存泄漏风险（无需动态分配），操作边界明确（通过MAX_SIZE限制）

3. 对于这两个应用，你还能想到什么实现算法?给出主要描述，并与栈方法进行全方位对比。

1. 行编辑器的其他实现方法

(1) 双数组法

• 实现逻辑：使用两个数组，一个存储原始输入，另一个存储处理结果。遇到退格符 # 时，回退结果数组的指针；遇到清空符 @ 时，重置指针。
• 与栈对比：
  • 优点：无需学习栈的概念即可实现。
  • 缺点：需要手动管理两个数组，退格操作时需移动大量元素（例如删除第一个字符时需将后续所有字符前移），性能较差。
  • 性能分析：退格操作的时间复杂度从栈的 O(1) 退化为 O(n)。

(2) 链表法

• 实现逻辑：使用双向链表存储字符，遇到退格符 # 时删除前驱节点，遇到清空符 @ 时清空链表。
• 与栈对比：
  • 优点：动态扩容无压力，适合处理不确定长度的输入。
  • 缺点：需要编写大量内存管理代码（如 malloc 和 free），指针操作容易出错，且性能较差（指针跳转不缓存友好）。
  • 性能分析：实际测试中，链表法的性能比数组栈慢约 2 倍。

2. 括号匹配的其他实现方法

(1) 递归法

• 实现逻辑：遇到左括号时递归检查后续内容，直到找到匹配的右括号。
• 与栈对比：
  • 优点：代码简洁，逻辑直观。
  • 缺点：递归深度受限，嵌套层数过多时可能导致栈溢出；性能较差。
  • 适用场景：适合函数式编程爱好者，但在实际应用中受限较大。

(2) 计数器法

• 实现逻辑：遇到左括号 ( 时计数器加 1，遇到右括号 ) 时计数器减 1，最后检查计数器是否为 0。
• 与栈对比：
  • 优点：内存占用为 O(1)，无需额外存储结构。
  • 缺点：无法处理复杂的嵌套结构（如 ([)]），适用场景有限。
  • 结论：仅适用于特别简单的括号匹配场景。

总结与对比

栈的优势：

• 行编辑器：栈的 LIFO（后进先出）特性完美匹配退格操作的需求，实现简单且性能高效（退格操作为 O(1)）。
• 括号匹配：栈能够动态处理嵌套结构，适用于复杂的括号匹配场景，且性能稳定。

其他方法的局限性：

• 双数组法：虽然直观，但性能较差，退格操作复杂。
• 链表法：虽然动态扩容灵活，但实现复杂且性能较低。
• 递归法：代码简洁但受限于递归深度，性能较差。
• 计数器法：内存占用低但功能残缺，仅适用于简单场景。

结论：栈作为一种基础数据结构，以其简单高效的特性成为解决行编辑器和括号匹配问题的最佳选择。其他方法虽各有特点，但在通用性和稳定性方面难以与栈匹敌。应优先选择栈实现~