20162323周楠 2017-2018-1 《程序设计与数据结构》第十周学习总结

目录预览

0.教材学习内容总结
1.教材学习中的问题和解决过程
2.代码调试中的问题和解决过程
3.代码托管
4.结对及互评
5.其他（感悟、思考等，可选）
6.学习进度条

0.教材学习内容总结

19.1 无向图

允许树中的每个结点与多个其他结点相连接，并且不分父结点与子结点，则得到的就是图
图由结点及结点间的连接组成，图中，结点成为顶点，结点间的连接为边
无向图中，表示边的的顶点对是无序的
堆的三个基本操作：向堆中添加一个新元素、找到最大值和删除最大值
无向图：表示边的顶点对是无序的图
如果图中的两个顶点之间有边连接，则称它们是邻接的
邻居：邻接点
自循环（悬挂）：图中自己连接到自己的边

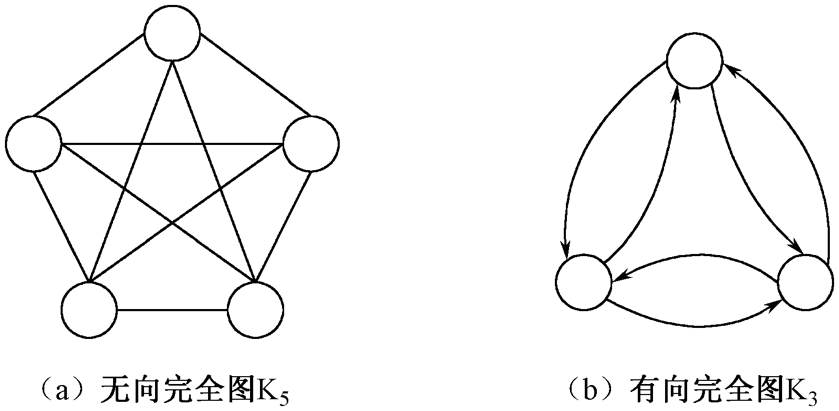
一、完全图

如果无向图中连接顶点的边数达到最大，则图为完全图
路径是图中连接两个顶点的边的序列
如果无向图中任意两个顶点间都有路径，则无向图称为连通的
第一个顶点和最后一个顶点相同且边不重复的路径称为环

19.2 有向图

有向图中，边是顶点的有序对
有向图中的路径是连接图中两个顶点的有向边的序列
拓扑序
有向图的特性
1.任何顶点到根都没有连接
2.到达每个非根元素的连接都只有一个
3.从根到每个顶点都有路径

19.3 带权图

带权图：图中每条边上都有对应的权值的图，也叫网络
有向带权图与无向带权图

19.4 常用的图算法

一、遍历

使用数组实现的图的广度优先遍历的迭代算法

图的深度优先遍历与广度优先遍历的主要差异在于用栈代替队列来管理遍历过程

二、测试连通性

当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所含的顶点数时，图是连通的

三、最小生成树

生成树是包含图中所有顶点及图中部分（可能不是全部）边的一棵树
最小生成树是其所含边的权值之和小于等于图的任意其他其他生成树的边的权值之和的生成树

四、判定最短路径

最短路径是在带权图中找到最短路径

19.5 图的实现策略

一、邻接表

二、邻接矩阵

1.教材学习中的问题和解决过程

- 问题：如何判断有向图里的相同的环？ - 解答：首先去掉开始或者结尾的节点编号，使得每个节点只出现一次；每个环找编号最小的点作为起点，前后两个节点（如果有）选择小的作为第二个节点，这样每个环就得到一致的编号了

2.代码调试中的问题和解决过程

- 问题：![](http://images2017.cnblogs.com/blog/1062821/201710/1062821-20171022170952365-2062662492.png)

3.代码托管

[代码托管](https://git.oschina.net/GiggleZN)

4.结对及互评

### 点评模板： - 博客中值得学习的或问题： - 会有自己的笔记 ### 本周结对学习情况 - [20162322朱娅霖](http://www.cnblogs.com/zyl905487045/) - 结对学习内容 - 一起做实验

5.其他（感悟、思考等，可选）

本周学习收获来自于实验和老师的课堂讲解学习。实验的内容很丰富，在夯实基础的同时，也加深我们对知识的理解和掌握。课堂讲解其实对我个人的帮助也是非常大的. ***

6.学习进度条

| | 代码行数（新增/累积）| 博客量（新增/累积）|学习时间（新增/累积）|重要成长| | -------- | :----------------:|:----------------:|:---------------: |:-----:| | 目标 | 5000行 | 30篇 | 400小时 | | | 第一周 |0行 | 6/6 | 20/20 | | | 第二周 | 258/258 | 5/11 | 17/37 | | | 第三周 | 687/945 | 9/20 | 17/54 | | | 第四周 | 798/1743 | 23/43 | 15/69 | | | 第五周 | 362/2105 | 12/55 | 15/69 | |

posted on 2017-11-12 15:56 GiggleKV 阅读(500) 评论(0) 收藏举报

刷新页面返回顶部