学习总结-快速傅里叶变换(FastFourierTransform)
\(update\ on\ 2020.9.11:\)增加了“实战演练”(放题解的地方)
\(update\ on\ 2021.7.31:\)增加了分治法
(〇)前言
快速傅里叶变换(Fast Fourier Transform, FFT),是快速计算序列的离散傅里叶变换(DFT)或其逆变换的方法。FFT会通过把DFT矩阵分解为稀疏(大多为零)因子之积来快速计算此类变换。因此,它能够将计算DFT的复杂度从只用DFT定义计算需要的复杂度\(\Theta(N^2)\),降低到\(\Theta(N\log N)\),其中\(N\)为数据大小。
快速傅里叶变换广泛的应用于工程、科学和数学领域。这里的基本思想在1965年才得到普及,但早在1805年就已推导出来。1994年美国数学家吉尔伯特·斯特朗把FFT描述为“我们一生中最重要的数值算法”,它还被IEEE科学与工程计算期刊列入20世纪十大算法。
不要管上面那段话。作为OIer,我们的关注点应该只有两个:
-
离散傅里叶变换(DFT)是什么
-
时间复杂度\(\Theta(N^2)\to\Theta(N\log N)\)
现在就由小编带领大家快速入门FFT。
前置知识:实数的运算(逃
(一)从多项式到卷积
1.1多项式的系数表示法与点值表示法
多项式(Polynomial)是代数学中的基础概念,是由称为未知数的变量和称为系数的常数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。
多项式是整式的一种。未知数只有一个的多项式称为一元多项式。下文讨论的多项式指一元多项式。
给出一个多项式:
不难发现,当\(a_0,a_1,...,a_{N-1}\)确定了以后,多项式\(A(x)\)也就确定了。因此,我们可以用\((a_0,a_1,...,a_{N-1})\)来表示一个多项式。这就是多项式的系数表示法。
将\(N\)个互不相同的\(x\),分别为\((x_0,x_1,...,x_{N-1})\)(称为插值节点),带入到多项式\(A(x)\)中,就可以得到\(N\)组值,分别为\((A(x_0),A(x_1),...,A(x_{N-1}))\),或者表示为\((y_0,y_1,...,y_{N-1})\)。这样一来,多项式也随之确定。这就是多项式的点值表示法。
理解点值表示法可以参考\(N\)元一次方程组。把\(N\)个\(x\)不同的取值带进去,就得到了\(N\)个\(N\)元一次方程。分别为:
\(\begin{bmatrix}x_0^0a_0,&x_0^1a_1,&...,&x_0^{N-2}a_{N-2},&x_0^{N-1}a_{N-1}\\x_1^0a_0&x_1^1a_1,&...,&x_1^{N-2}a_{N-2},&x_1^{N-1}a_{N-1}\\\vdots&\vdots&\vdots&\vdots&\vdots\\x_{N-1}^0a_{0}&x_{N-1}^1a_1&...,&x_{N-1}^{N-2}a_{N-2}&x_{N-1}^{N-1}a_{N-1}\end{bmatrix}=\begin{bmatrix}y_0\\y_1\\\vdots\\y_{N-1}\end{bmatrix}\)
于是\(a_0,a_1,...,a_{N-1}\)都唯一确定了,即多项式也唯一确定了。解出上述方程就能求得系数表示法下的多项式了。
在这里有一个重要的结论:系数表示法和点值表示法是可以相互转化的。
1.2多项式乘法与卷积
现在有两个多项式\(A(x)=\sum\limits_{i=0}^{N-1}a_ix^i,B(x)=\sum\limits_{i=0}^{M-1}b_ix^i\)
如果我们把上述两个多项式乘起来,那么我们就会得到一个\(N+M-2\)次多项式。设这个多项式为\(C(x)\)
那么,
解释一下:由于\(C(x)\)是一个\(N+M-2\)次多项式,那么他的所有项的次数就为\(0,1,2...N+M-4,N+M-3,N+M-2\)。因此我们只需要枚举每一项的次数,算出该项的系数就行了。
举个例子:
\(c_5x^5=a_0x^0b_5x^5+a_1x^1b_4x^4+...+a_5x^5b_0x^0=(a_0b_5+a_1b_4+...+a_5b_0)x^5\)
以上就是多项式乘法。实际上就是将两个多项式的项两两相乘,简记为\(C=A*B\)。
接下来就是乘法的本质——卷积。
设\(c_k\)为\(C\)的第\(k\)项的系数。\(a_k,b_k\)同理。
由多项式乘法可以得到:
形如\(c_k=\sum\limits_{i\oplus j=k}a_ib_j\)的式子称为卷积,其中\(\oplus\)是某种运算。多项式乘法实际上就是加法卷积。
卷积还可以写作函数的形式,就像\(C=A*B\)。
介绍另一种卷积:狄利克雷卷积(在我的学习总结-莫比乌斯反演中有描述)
狄利克雷卷积是乘法卷积(\(d|N\)实际上就是\(i\times j=N,i=d,j=\dfrac{N}{d}\))
1.3求解多项式乘法
求多项式\(C=A*B\)。
方法很简单,直接按照定义计算就行了。给出代码:
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
c[i+j] += a[i]*b[j];
就是上面这个入门难度的东西啦。时间复杂度:\(\Theta(N^2)\)
然而,讲这么简单的东西干什么。是因为——这个东东可以用FFT优化到\(\Theta(N\log N)\)!没错,一开始我听说这个东西的时候也很震惊:这玩意儿还能优化?
欲后事如何,且听下回分解。
(二)复数的引入
写本章时学校突然断电,然后gg
2.1奇妙的分治
珂学家们经过研究发现,当用点值表示多项式的时候,有一些好用的性质:
对于一组插值节点\((x_0, x_1, x_2,...,x_{N-1}),\)
多项式\(A\)的值为\((A(x_0),A(x_1),A(x_2),...,A(x_{N-1}))\)
多项式\(B\)的值为\((B(x_0),B(x_1),B(x_2),...,B(x_{N-1}))\)
多项式\(C=A*B\)的值为\((C(x_0),C(x_1),C(x_2),...,C(x_{N-1}))\)
那么,有\(C(x_0)=A(x_0)\times B(x_0),C(x_1)=A(x_1)\times B(x_1),...,C(x_{N-1})=A(x_{N-1})\times B(x_{N-1}))\)
也就是说,在点值表示法下,我们可以\(\Theta(N)\)求出两个多项式的乘积。
然而,多项式一般是用系数表示法表示的。问题就转化为了:如何快速将多项式从系数表示法转化为点值表示法,在求得乘积后,如何快速将点值表示法转化为系数表示法。
我们知道,系数表示法转点值表示法要通过插入\(N\)个不同的插值节点。而每次插值的时间复杂度是\(\Theta(N)\),总时间复杂度就是\(\Theta(N^2)\),我们貌似又回到了起点。
此时,珂学家又提出了一个算法:分治。即将一个多项式\(A\)按照项的奇偶性分为两个子问题求解。于是就有了(假设多项式的项数\(N\)为\(2^k\)):
\(A(x)=(a_0x^0+a_2x^2+a_4x^4+...+a_{N-2}x^{N-2})+(a_1x^1+a_3x^3+a_5x^5+...+a_{N-1}x^{N-1})\)
\(=(a_0x^0+a_2x^2+a_4x^4+...+a_{N-2}x^{N-2})+x(a_1x^0+a_3x^2+a_5x^4+...+a_{N-1}x^{N-2})\)
设:
可以得到:
这时候,
拆开看一看:
如果直接这样计算的话,需要计算4次多项式乘法。
时间复杂度为 \(T(N)=\Theta(N)+4T(\frac{N}{2})\),大概是 \(\Theta(N^2)\)。
然而还可以继续化简:
乍一看貌似更复杂了,事实上不难发现,计算这个式子只需要三次多项式乘法。
时间复杂度为 \(T(N)=\Theta(N)+3T(\frac{N}{2})\),大约是 \(\Theta(N^{1.47})\),十分优秀。
2.2为什么要引入复数
当我们在算\(x\)的时候,用到了\(x^2\)的插值结果。如果\(x^2\)也是插值节点,是否可以直接调用?
我们可以想象一下我们需要怎样的插值节点:
- 如果\(x\)存在,那么\(x^2\)也存在。
- 插值节点的个数要等于\(N\)
可以从复平面内找到这\(N\)个特殊的插值节点。
以上是引入复数的原因。
2.3复数的基本认识
(1)复数
复数,为实数的延伸,它使任一多项式方程都有根。
复数当中有个“虚数单位”\(i\),它是\(-1\)的一个平方根,即\(i^2=-1\)。任一复数都可表达为\(a+bi\),其中\(a\)及\(b\)皆为实数,分别称为复数之“实部”和“虚部”。
每个复数都对应了平面上的一个向量\((a,b)\),这个平面叫做复平面,它是由水平的实轴与垂直的虚轴建立起来的复数的几何表示。
故每一个复数唯一对应了一个复平面上的向量,每一个复平面上的向量也唯一对应了一个复数。其中\(0\)既被认为是实数,也被认为是虚数。
复数\(z\)的模长\(|z|\)定义为\(z\)在复平面到原点的距离,\(|z|=\sqrt{a^2+b^2}\)。幅角\(\theta\)为实轴的正半轴正方向(逆时针)旋转到\(z\)的有向角度。
由于虚数无法比较大小。复数之间的大小关系只存在等于与不等于两种关系,两个复数相等当且仅当实部虚部对应相等。对于虚部为\(0\)的复数之间是可以比较大小的,相当于实数之间的比较。
复数之间的运算满足结合律,交换律和分配律。由此定义复数之间的运算法则:
复数运算的加法满足平行四边形法则,乘法满足幅角相加,模长相乘。
对于一个复数\(z=a+bi\),它的共轭复数是\(z'=a-bi\),\(z'\)称为\(z\)的复共轭。
共轭复数有一些性质:
\(z\cdot z'=a^2+b^2\)
\(|z|=|z'|\)
复数类的代码实现(仅供参考):
struct Complex{
double r, i;
Complex() {}
Complex(double r, double i): r(r), i(i) {}
inline Complex operator +(const Complex& x) const {
return Complex(r + x.r, i + x.i);
}
inline Complex operator -(const Complex& x) const {
return Complex(r - x.r, i - x.i);
}
inline Complex operator *(const Complex& x) const {
return Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline void operator *=(const Complex& x) {
*this = Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline Complex conj(){
return Complex(r, -i);
}
};
(2)单位根
下图是复数中的单位圆。
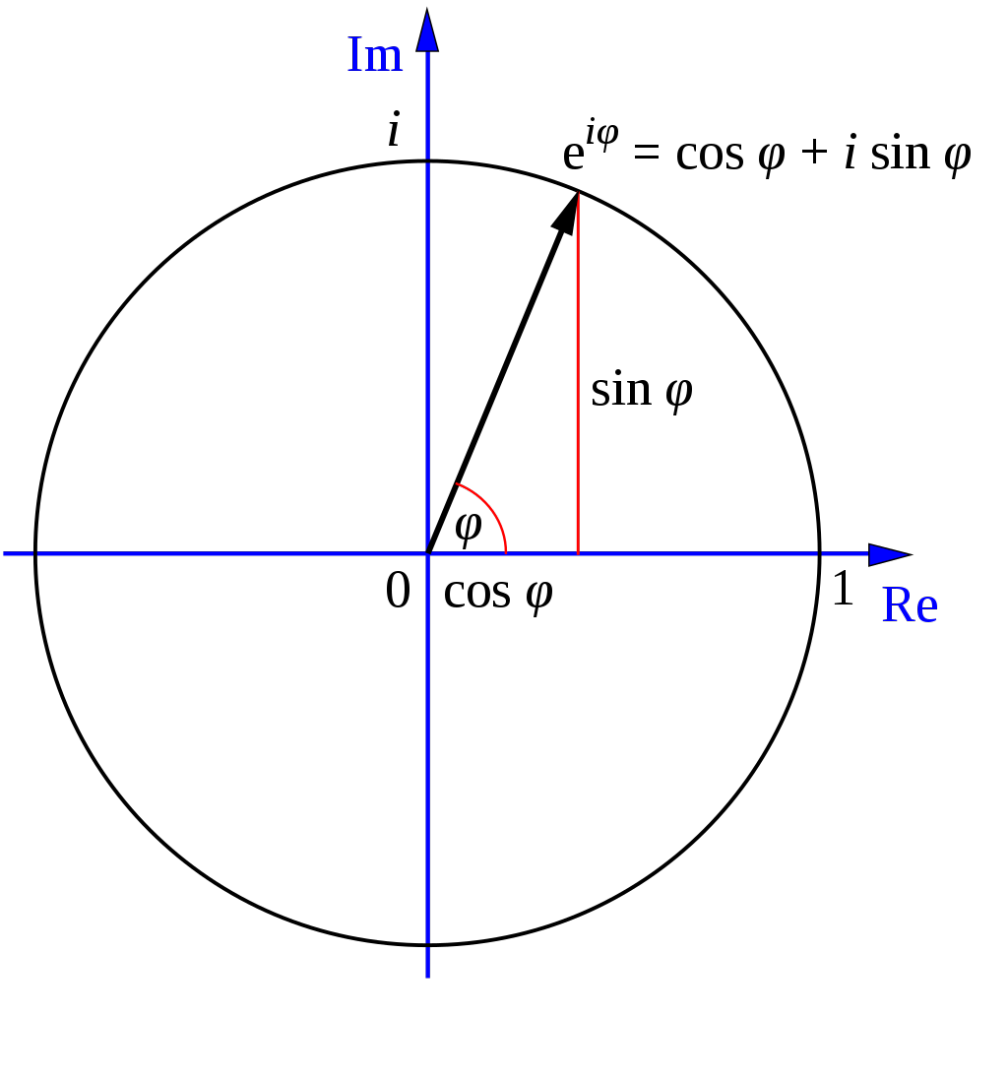
根据欧拉幅角公式,\(e^{i\varphi}=\cos\varphi+i\sin\varphi\)
我们发现单位圆上的复数(设幅角为\(\varphi\))可以表示为\(e^{i\varphi}\)。
将单位圆等分成\(N\)个部分(以单位圆与实轴正半轴的交点一个等分点),以原点为起点,圆的这\(N\)个\(N\)等分点为终点,作出\(N\)个向量。这\(N\)个向量就是复数的单位根啦。
其中幅角为正且最小的向量称之为\(N\)次单位向量,记为\(\omega_n^1\)。
以此类推,\(N\)个向量分别为\(\omega_n^1,\omega_n^2,\omega_n^3,...,\omega_n^n\),它们可以用复数之间的乘法得来\(\omega_n^k=\omega_n^{k-1}\cdot\omega_n^1(2\leq k\leq n)\)
显然\(\omega_n^0=\omega_n^n=1\)
\(\omega_n^k\)也可以写作\(e^{i\cdot \frac{2k\pi}{n}}\)
所以\(\omega_n^k=\cos(\dfrac{2k\pi}{n})+i\sin(\dfrac{2k\pi}{n})\)
\(\omega_n^k\)有两个重要的性质:
- 性质1:折半引理
由几何意义可以知道,这两者表示的向量终点是一样的。
同样可以用三角恒等变换证明。
- 性质2:消去引理
由几何意义可以知道,两者表示的向量模长相等,方向相反。
也可以用三角恒等变换证明。
这里给出求\(\omega_n^k\)的代码实现:
omega[i] = Complex(cos(2.0*PI/N*i), sin(2.0*PI/N*i));
(三)快速傅里叶变换(Fast Fourier Transform)
3.1离散傅里叶变换(Discrete Fourier Transform)
(1)理论分析
步入正题。如何使用复数加速插值。
相信经过上一张的讨论,大家心里都已经清楚2.1中提到的这\(N\)个特殊的复数是什么了。这\(N\)个复数正是复数的单位根。
不难发现,复数的\(N\)个单位根恰好满足了我们“理想”中插值节点的所有条件。温习一下:
- 如果\(x\)存在,那么\(x^2\)也存在。
- 插值节点的个数要等于\(N\)
接下来我们要将这\(N\)个单位根带入2.1中推导出的公式。公式如下:
分为两种情况:
设\(0\leq k<\dfrac{n}{2}\),则大于等于\(\dfrac{n}{2}\)的数可以表示为\(k+\dfrac{n}{2}\)
- 对于\(0\leq k<\dfrac{n}{2}\)的部分
\(A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^{k}A_2(\omega_n^{2k})\)
由折半引理得:\(\omega_n^{2k}=\omega_\frac{n}{2}^k\)
\(\therefore A(\omega_n^k)=A_1(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_2(\omega_\frac{n}{2}^k)\)
- 对于\(\dfrac{n}{2}\leq k+\dfrac{n}{2}<n\)的部分
\(A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_{n}^{2k+n})+\omega_{n}^{k+\frac{n}{2}}A_2(\omega_n^{2k+n})\)
由消去引理得:\(\omega_n^{2k+n}=\omega_n^{2k},\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)
由折半引理得:\(\omega_n^{2k}=\omega_\frac{n}{2}^{k}\)
\(\therefore A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_\frac{n}{2}^{k})-\omega_n^kA_2(\omega_\frac{n}{2}^k)\)
把上述两个式子合起来:
依照上面那条式子,我们就能以\(\Theta(N)\)的时间复杂度带入每一个根\(\omega_n^k\),然后转化为子问题\(A_1,A_2\)求解。\(A_1,A_2\)的规模都是原问题的一半,因此,时间复杂度为:
\(T(n)=2T(\dfrac{N}{2})+\Theta(N)=\Theta(N\log_2 N)\)
以上是离散傅里叶变换的理论,可以快速将系数表示法转化为点值表示法。
(2)程序实现
上述操作可以通过递归实现。下面给出C++代码:
代码中的部分细节:
\(\operatorname{Complex}\)是自己封装的复数类(用\(\operatorname{STL}\)也可以,不过比较慢)
\(\operatorname{omega}\)是预处理出来的\(\omega\)值,\(\operatorname{omega}[k]\)存的是\(\omega_n^k\)的值。
由于在递归的过程中\(n\)会改变,设\(n\)改变后变为\(len\),那么根据折半引理,\(\omega_{len}^k=\omega_{n}^{\frac{n}{len}k}\)
代码应该还是比较清晰的。
void transform(Complex *a, const int& len, const Complex* omega, const int& N){
if(len == 1) return ;
int mid = len>>1;
for(int i=0; i<len; i++) save[i] = a[i];
Complex *al = a, *ar = a + mid;
for(int i=0; i<len/2; i++) al[i] = save[i<<1], ar[i] = save[i<<1|1];
transform(al, len>>1, omega, N), transform(ar, len>>1, omega, N);
for(int i=0; i<len/2; i++){
save[i] = al[i] + ar[i]*omega[N/len*i];
save[i+len/2] = al[i] - ar[i]*omega[N/len*i];
}
for(int i=0; i<len; i++) a[i] = save[i];
}
以上。
3.2离散傅里叶反变换(Inverse Discrete Fourier Transform)
(1)理论分析
有了DFT(离散傅里叶变换)还不够,我们还需要将点值表示法转化为系数表示法。这时候,我们就需要用到IDFT(离散傅里叶反变换)。
也就是我们要从\((A(x_0),A(x_1),A(x_2),...,A(x_{n-1}))\)推导出系数\((a_0,a_1,a_2,...,a_{n-1})\)
进入莫比乌斯反演模式
先将\((a_0,a_1,a_2,...,a_{n-1})\)做DFT,得到\((b_0,b_1,b_2,...,b_{n-1})\)
写成多项式形式:\(B(x)=\sum\limits_{i=0}^{n-1}b_ix^i\),有:
将\(x=\omega_n^{-k}\)带入\(B(x)\),得到一组点值\((c_0,c_1,c_2, ...,c_{n-1})\)
就得到了这样的式子:
然后将两式合并:
\(c_k=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}a_j\cdot(\omega_n^i)^j\cdot(\omega_i^{-k})^i\)
\(=\sum\limits_{j=0}^{n-1}a_j\sum\limits_{i=0}^{n-1}(\omega_n^{-k})^i\cdot(\omega_n^{i})^j\)
\(=\sum\limits_{j=0}^{n-1}a_j\sum\limits_{i=0}^{n-1}\omega_n^{ij-ki}\)
\(=\sum\limits_{j=0}^{n-1}a_j\sum\limits_{i=0}^{n-1}(\omega_n^{i})^{j-k}\)
设\(\delta =j-k,S(j,k)=\sum\limits_{i=0}^{n-1}(\omega_n^i)^\delta=\sum\limits_{i=0}^{n-1}(\omega_n^\delta)^i\)
-
当\(\omega_n^\delta=1\)时,\(\delta=0,j=k,S(j,k)=n\)
-
当\(\omega_n^\delta\not=1\)时,根据等比数列求和公式,\(S(j,k)=\dfrac{\omega_n^0[(\omega_n^\delta)^{n}-1]}{\omega_n^\delta-1}=\dfrac{1\times[(\omega_n^n)^{\delta}-1]}{\omega_n^\delta-1}=\dfrac{1-1}{\omega_n^\delta-1}=0\)
\(\therefore c_k=\sum\limits_{j=0}^{n-1}a_j\cdot n\cdot[j=k]=a_k\cdot n\)
神奇的事情发生了...我们得到了一个十分简洁美丽的公式:
其中\(c_k\)是插值节点\(\omega_n^{-k}\)代入到\(B(x)\)后得到的值。
以上就是IDFT的理论。
简单地说,DFT就是用\(\omega_n^k\)插值系数表达得到点值表达,IDFT就是用\(\omega_n^{-k}\)插值系数表达得到点值表达。
(2)代码实现
与DFT的实现除了插值变为了\(\omega_n^{-k}\)以外完全相同(当然得到的结果还要除以\(n\))。
给出调用的代码:
\(\operatorname{omegaInverse}\)数组指的是\(\omega_n^{-k}\),直接用共轭复数的求法就可以求出。(详细见2.2(1))
void idft(Complex *a, const int& N){
transform(a, N, omegaInverse, N);
for(int i=0; i<N; i++) a[i]/=N;
}
以上。
3.3FFT加速多项式乘法
所谓FFT,其实就是将DFT和IDFT合起来。下面是加速多项式乘法的流程:
- 使用DFT,将\(A(x),B(x)\)转为点值表示。复杂度\(\Theta(N\log N)\)
- 在点值表示下将两个多项式相乘,得到\(C(x)\)的点值表示。复杂度\(\Theta(N)\)
- 使用IDFT,将\(C(x)\)转为系数表示。复杂度\(\Theta(N\log N)\)
FFT总之间复杂度\(\Theta(N\log N)\),而且常数较大。
下面是递归FFT的代码实现(上文大部分已经解释过了):
网上大部分题解的递归FFT都无法通过模板多项式乘法
因为已经预处理出了\(\omega_n^k\)和\(\omega_n^{-k}\),下面的程序常数较小,实测可以通过。
#include<bits/stdc++.h>
using namespace std;
const double PI = 3.1415926535;
const int maxn = 4e6 + 5;
inline double read(){
int w = 0, f = 1; char ch = getchar();
while(ch < '0' or ch > '9') {if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' and ch <= '9') w = w*10 + ch - '0', ch = getchar();
return (double)w*f;
}
struct Complex{
double r, i;
Complex() {}
Complex(double r, double i): r(r), i(i) {}
inline Complex operator +(const Complex& x) const {
return Complex(r + x.r, i + x.i);
}
inline Complex operator -(const Complex& x) const {
return Complex(r - x.r, i - x.i);
}
inline Complex operator *(const Complex& x) const {
return Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline void operator *=(const Complex& x) {
*this = Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline Complex conj(){
return Complex(r, -i);
}
}A[maxn], B[maxn], C[maxn];
struct FastFourierTransform{
Complex omega[maxn], omegaInverse[maxn], save[maxn];
void init(const int& N){
for(int i=0; i<N; i++){
omega[i] = Complex(cos(2.0*PI/N*i), sin(2.0*PI/N*i));
omegaInverse[i] = omega[i].conj();
}
}
void transform(Complex *a, const int& len, const Complex* omega, const int& N){
if(len == 1) return ;
int mid = len>>1;
for(int i=0; i<len; i++) save[i] = a[i];
Complex *al = a, *ar = a + mid;
for(int i=0; i<len/2; i++) al[i] = save[i<<1], ar[i] = save[i<<1|1];
transform(al, len>>1, omega, N), transform(ar, len>>1, omega, N);
for(int i=0; i<len/2; i++){
save[i] = al[i] + ar[i]*omega[N/len*i];
save[i+len/2] = al[i] - ar[i]*omega[N/len*i];
}
for(int i=0; i<len; i++) a[i] = save[i];
}
void dft(Complex *a, const int& N){
transform(a, N, omega, N);
}
void idft(Complex *a, const int& N){
transform(a, N, omegaInverse, N);
}
}fft;
int main(){
int N, M;
N = read(), M = read();
for(int i=0; i<=N; i++) A[i].r = read();
for(int j=0; j<=M; j++) B[j].r = read();
int limit = 1;
while(limit <= N+M) limit <<= 1;
fft.init(limit);
fft.dft(A, limit); fft.dft(B, limit);
for(int i=0; i<limit; i++) C[i] = A[i]*B[i];
fft.idft(C, limit);
for(int i=0; i<=N+M; i++) printf("%d ", (int)(C[i].r/limit + 0.5));
return 0;
}
以上。其实到这里已经可以了但我们要追求极致的效率。
3.4精细FFT
为什么叫精细FFT呢因为它很精细呀。为了追求极致的效率,我们选择对上文的递归实现FFT进行卡常优化。
(1)蝴蝶操作
操作的名称由来是因为这个操作很像蝴蝶飞舞(可以想象这个操作是多么的秀)。
观察下图,显示了递归的过程。将序号转为二进制。
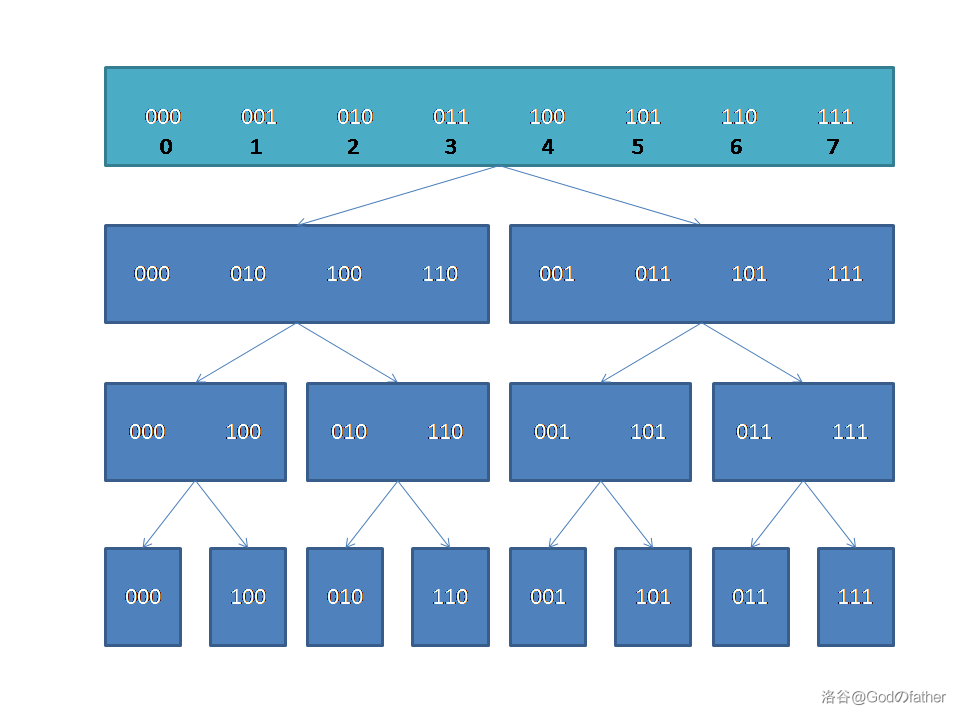
不难发现,递归最底层的数所在的位置恰好是值的二进制翻转。
比如说,\(6\)的二进制是\(110\),而它在递归底层的位置是\(3\),二进制是\(011\),恰好是\(6\)的二进制的翻转。
据此,我们可以将最底层的所有值的位置确定,然后逐层向上合并,这样能够大大减小常数。这就是蝴蝶操作。
问题来了,如何求某个数的二进制翻转。
用类似于数位DP的方式,设\(\operatorname{reserve(x)}\)表示\(x\)的二进制翻转。
- 当\(x\)的二进制最后一位为\(1\)时,
reserve[x]=reserve[x>>1]>>1|(N>>1);
- 当\(x\)的二进制最后一位为\(0\)时,
reserve[x]=reserve[x>>1]>>1;
合起来就是:
reserve[x] = (reserve[x>>1]>>1)|((x&1)?N>>1:0);
解释一下,如果我们要翻转一个\(x\)位的二进制数,就要把最后一位拿出来,把剩下的\(x-1\)位翻转,再把拿出来的最后一位放到第一位。如下:
@****1
拿走1,变成 @****
翻转,变成 ****@
把1放回,变成 1****@
代码上面已经有了。
(2)三步变两步
观察复数的乘法:
\((a+bi)^2=a^2+2abi-b^2\)
设多项式\(P(x)=A(x)+iB(x)\)
那么\(P(x)^2=(A(x)^2+iB(x)^2)=A(x)^2-B(x)^2+2A(x)B(x)i\)
我们发现,多项式\(C=A*B\)的两倍恰好就是\(P(x)^2\)的虚部!
因此我们只需要把\(A(x)\)当做\(P(x)\)的实部,\(B(x)\)当做\(P(x)\)的虚部,然后求\(P(x)^2\),就能将\(C(x)\)求出啦。
这样就只做了一次DFT,一次IDFT,由三步变为了两步。
奉上本人最精细的FFT:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e6 + 5;
inline double read(){
int w = 0, f = 1; char ch = getchar();
while(ch < '0' or ch > '9') {if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' and ch <= '9') w = w*10 + ch - '0', ch = getchar();
return (double)w*f;
}
double PI = 3.1415926535;
struct Complex{
double r, i;
Complex() {}
Complex(double r, double i) : r(r), i(i) {}
inline void real(const double& x) {r = x;}
inline double real() {return r;}
inline Complex operator + (const Complex& rhs) const {
return Complex(r + rhs.r, i + rhs.i);
}
inline Complex operator - (const Complex& rhs) const {
return Complex(r - rhs.r, i - rhs.i);
}
inline Complex operator * (const Complex& rhs) const {
return Complex(r*rhs.r - i*rhs.i, r*rhs.i + i*rhs.r);
}
inline void operator /= (const double &x) {
r /= x, i /= x;
}
inline void operator *= (const Complex& rhs) {
*this = Complex(r*rhs.r - i*rhs.i, r*rhs.i + i*rhs.r);
}
inline void operator += (const Complex& rhs) {
r += rhs.r, i += rhs.i;
}
inline Complex conj() {
return Complex(r, -i);
}
};
struct FastFourierTransform{
Complex omega[maxn], omegaInverse[maxn]; int reserve[maxn];
void init(const int& N){
for(int i=0; i<N; i++){
omega[i] = Complex(cos(2*PI/N*i), sin(2*PI/N*i));
omegaInverse[i] = omega[i].conj();
reserve[i] = (reserve[i>>1]>>1)|((i&1)?N>>1:0);
}
}
void transform(Complex *a, const int& N, const Complex* omega){
for(int i=0; i<N; i++) if(reserve[i] > i) swap(a[reserve[i]], a[i]);
for(int l=2; l<=N; l<<=1){
int m = l/2;
for(int j = 0; j < N; j += l){
for(int i=0; i<m; i++) {
Complex t = omega[N/l*i] * a[j+m+i];
a[j+m+i] = a[j + i] - t;
a[j + i] = a[j + i] + t;
}
}
}
}
void dft(Complex *a, const int& N){
transform(a, N, omega);
}
void idft(Complex *a, const int& N){
transform(a, N, omegaInverse);
}
}fft;
Complex F[maxn];
int main(){
int N, M;
N = read(), M = read();
for(int i=0; i<=N; i++) F[i].r = read();
for(int j=0; j<=M; j++) F[j].i = read();
int limit = 1;
while(limit <= N+M) limit <<= 1;
fft.init(limit);
fft.dft(F, limit);
for(int i=0; i<limit; i++) F[i] = F[i]*F[i];
fft.idft(F, limit);
for(int i=0; i<=N+M; i++) printf("%d ", (int)(F[i].i/limit/2 + 0.5));
return 0;
}
以上。全剧终。
(四)实战演练
经过了社会的毒打我发现了解FFT和使用FFT是两回事,于是便有了这一章...
1.1[ZJOI2014]力
题目是求\(E_i\)的值:
\(F_j=\sum\limits_{i=1}^{j-1}\dfrac{q_i\times q_j}{(i-j)^2}-\sum\limits_{i=j+1}^{n}\dfrac{q_i\times q_j}{(i-j)^2},E_i=\dfrac{F_i}{q_i}\)
第一眼看上去:这跟FFT有什么关系?——哦,原来要化简。
那就化简吧:
\(E_j=\dfrac{F_j}{q_j}=\sum\limits_{i=1}^{j-1}\dfrac{q_i}{(j-i)^2}-\sum\limits_{i=1}^{n-j}\dfrac{q_{i+j}}{i^2}\)
观察前面的式子\(\sum\limits_{i=1}^{j-1}\dfrac{q_i}{(j-i)^2}\),如果设\(f(i)=q_i,g(i)=\dfrac{1}{i^2}\),那么就变成了:
\(\sum\limits_{i=1}^{j-1}f(i)g(j-i)\),写好看一点:
为了不影响结果,我们要令\(g(0)=0,f(j)=0\)。
上面的式子其实已经变成了卷积的形式。FFT的作用是求多项式乘法,多项式乘法事实上就是卷积。
也就是说,上面那个东西可以用FFT算出来(与多项式乘法无异)。
但是后面还有一个式子:\(\sum\limits_{i=1}^{n-j}\dfrac{q_{i+j}}{i^2}\)
,让它顺眼一点:
同样为了保证不影响结果,我们要令\(f(j)=0,g(0)=0\)。
这个式子就有点神奇了,因为它没有\(i+j=k\)的形式(不是卷积的形式)。
然而这是有套路的。虽然\(i+j+i\not=n-j\),但是我们发现\(i+j-i=j\)。所以我们要想办法让\(i+j+i\to i+j-i\)。
两种方法:
-
令\(g'(n-i)=g(i)\),原式\(=\sum\limits_{i=0}^{n-j}f(i+j)g'(n-i)=\sum\limits_{i=0}^{n+j}f(i+j)g'(n-i)\)
-
令\(f'(n-i-j)=f(i+j)\),原式\(=\sum\limits_{i=0}^{n-j}f'(n-i-j)g(i)\)
其实就是将一个数组翻转,将差变为和。以上两种方法任君选择。
方法一需要注意的是,为了不影响结果,要保证\(\sum\limits_{i=n-j+1}^{n+j}f(i+j)g'(n-i)=0\)
最后,分别用FFT算出和式的结果后,作差即可。
两种方法在细节处理上略有差别。
附上代码(两种方法的代码都有):
(方法一)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 5;
const double PI = acos(-1);
struct Complex{
double r, i;
Complex () {}
Complex (double r, double i): r(r), i(i) {}
inline Complex operator +(const Complex& x) const{
return Complex(r + x.r, i + x.i);
}
inline Complex operator -(const Complex& x) const{
return Complex(r - x.r, i - x.i);
}
inline Complex operator *(const Complex& x) const{
return Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline void operator +=(const Complex& x){
*this = Complex(r + x.r, i + x.i);
}
inline void operator *=(const Complex& x){
*this = Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline Complex conj(){
return Complex(r, -i);
}
};
struct FastFourierTransform{
Complex omega[maxn], omegaInverse[maxn]; int reserve[maxn];
void init(const int& N){
for(int i=0; i<N; i++){
omega[i] = Complex(cos(2*PI/N*i), sin(2*PI/N*i));
omegaInverse[i] = omega[i].conj();
reserve[i] = (reserve[i>>1]>>1)|((i&1)?N>>1:0);
}
}
void transform(Complex *a, const int& N, const Complex* omega){
for(int i=0; i<N; i++) if(i > reserve[i]) swap(a[i], a[reserve[i]]);
for(int l=2; l<=N; l<<=1){
int m = l>>1;
for(Complex *p=a; p != a+N; p += l)
for(int i=0; i<m; i++){
Complex t = p[i+m]*omega[N/l*i];
p[i+m] = p[i] - t;
p[i] = p[i] + t;
}
}
}
void dft(Complex *a, const int& N){
transform(a, N, omega);
}
void idft(Complex *a, const int& N){
transform(a, N, omegaInverse);
}
}fft;
Complex q[maxn], g1[maxn], g2[maxn];
int main(){
int N;
scanf("%d", &N);
for(int i=1; i<=N; i++) scanf("%lf", &q[i].r);
for(int i=1; i<=N; i++) g1[i].r = 1.0/(double)i/i, g2[N-i].r = g1[i].r;
int limit = 1;
while(limit <= N<<1) limit <<= 1;
fft.init(limit);
fft.dft(g1, limit);
fft.dft(g2, limit);
fft.dft(q, limit);
for(int i=0; i<limit; i++) g1[i] = q[i]*g1[i];
for(int i=0; i<limit; i++) g2[i] = q[i]*g2[i];
fft.idft(g1, limit);
fft.idft(g2, limit);
for(int i=1; i<=N; i++){
printf("%.3lf\n", (g1[i].r - g2[N+i].r)/(double)limit);
}
return 0;
}
(方法二)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 5;
const double PI = acos(-1);
struct Complex{
double r, i;
Complex () {}
Complex (double r, double i): r(r), i(i) {}
inline Complex operator +(const Complex& x) const{
return Complex(r + x.r, i + x.i);
}
inline Complex operator -(const Complex& x) const{
return Complex(r - x.r, i - x.i);
}
inline Complex operator *(const Complex& x) const{
return Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline void operator +=(const Complex& x){
*this = Complex(r + x.r, i + x.i);
}
inline void operator *=(const Complex& x){
*this = Complex(r*x.r - i*x.i, r*x.i + i*x.r);
}
inline Complex conj(){
return Complex(r, -i);
}
};
struct FastFourierTransform{
Complex omega[maxn], omegaInverse[maxn]; int reserve[maxn];
void init(const int& N){
for(int i=0; i<N; i++){
omega[i] = Complex(cos(2*PI/N*i), sin(2*PI/N*i));
omegaInverse[i] = omega[i].conj();
reserve[i] = (reserve[i>>1]>>1)|((i&1)?N>>1:0);
}
}
void transform(Complex *a, const int& N, const Complex* omega){
for(int i=0; i<N; i++) if(i > reserve[i]) swap(a[i], a[reserve[i]]);
for(int l=2; l<=N; l<<=1){
int m = l>>1;
for(Complex *p=a; p != a+N; p += l)
for(int i=0; i<m; i++){
Complex t = p[i+m]*omega[N/l*i];
p[i+m] = p[i] - t;
p[i] = p[i] + t;
}
}
}
void dft(Complex *a, const int& N){
transform(a, N, omega);
}
void idft(Complex *a, const int& N){
transform(a, N, omegaInverse);
}
}fft;
Complex q1[maxn], q2[maxn], g[maxn];
int main(){
int N;
scanf("%d", &N);
for(int i=1; i<=N; i++) scanf("%lf", &q1[i].r), q2[N-i].r = q1[i].r;
for(int i=1; i<=N; i++) g[i].r = 1.0/((double)i*i);
int limit = 1;
while(limit <= N<<1) limit <<= 1;
fft.init(limit);
fft.dft(g, limit);
fft.dft(q1, limit);
fft.dft(q2, limit);
for(int i=0; i<limit; i++) q1[i] = q1[i]*g[i];
for(int i=0; i<limit; i++) q2[i] = q2[i]*g[i];
fft.idft(q1, limit);
fft.idft(q2, limit);
for(int i=1; i<=N; i++){
printf("%.3lf\n", (q1[i].r - q2[N-i].r)/(double)limit);
}
return 0;
}
未完待续...
(五)参考文献
上述1.和2.都是很好的文章,可以加深对FFT的理解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号