学习总结-从分块到莫队
(〇)写在前面的话
本文涉及到了分块以及依赖分块的离线算法——莫队。
众所周知,莫队是莫涛大神发明的算法,因此,在写总结之前,先orz莫涛大神。
前置知识(莫队):
-
双指针法(two pointers)*
-
分块*
注:带'*'号的下文会阐述
(一)根号数据结构——分块
1.1分块简介
一般来说,分块是在处理一些区间上的问题时经常用到的数据结构(当然,整数分块另当别论)。
就如本章标题“根号数据结构”,使用分块处理问题通常会带上一个根号。
分块的核心思想是,把整个序列分割成若干段,每一段成为“块”。每次询问或者修改一个区间的时候,就不需要单独的修改区间上的一个点,只需要修改区间涉及的每一个“块”。
块的长度是不固定的,一般取块长为\(\sqrt {N}\)(后文会解释)。
实际上,当块长为\(1\)的时候,其实就是一个点一个点地修改/查询。
1.2分块实现
先引入一个问题:
求一个数据结构,能支持区间/单点修改,区间/单点查询。设修改/查询区间为\([l,r]\)。
首先分类讨论,有以下两种情况:
- \(l\),\(r\)不在同一个块内
显然,\([l, r]\)涉及的块可以分为两种:
-
被\([l,r]\)完全包含(即该块为\([l,r]\)的子集)
-
与\([l,r]\)相交(即该块与\([l,r]\)有交集,但没有包含关系)
对于第一种情况,可以直接修改整个区间,这样做的时间复杂度为\(\Theta(\sqrt N)\)。因为最多只有\(\dfrac{N}{\sqrt N}=\sqrt N\)个块。
对于第二种情况,直接暴力将交集中的每一个点修改。这样做的时间复杂度是\(\Theta(\sqrt N)\),因为每个块最长只有\(\sqrt N\),且最多只有两个块与\([l,r]\)不存在包含关系。
- \(l\),\(r\)在同一个块内
直接暴力修改\([l,r]\)即可。时间复杂度为\(\Theta (\sqrt N)\),因为一个块最长为\(\sqrt N\)。
以上。
如果有\(M\)次修改或者查询操作,总时间复杂度为\(\Theta(M\sqrt N)\)。\(10^5\)以内的数据都能轻松跑过。
代码实现就不用说了,十分简单(在这个方面分块吊打许多数据结构)。
1.3时间复杂度分析
以下解释了为什么通常块长取\(\sqrt N\)。
不妨设块长为\(T\)。那么块的总数量就是\(\Theta (\dfrac{N}{T})\)。
对于各种操作的时间复杂度,上一节已经解释过了,这里不再解释。
区间修改的时间复杂度是\(\Theta (\max \{ \dfrac{N}{T},T\})\)
容易证明,当且仅当\(T=\sqrt N\)时,时间复杂度取得最小值,为\(\Theta(\sqrt N)\)。
注意,块的大小并不总是等于\(\sqrt N\)时,理论时间复杂度最优。具体问题要具体分析块的大小。
以上。
1.4整数分块
不同于序列上的分块。整数分块正如它的名字一样,是对某个整数进行分块。
整数分块的思想也与序列上的分块略有不同。整数分块是将一个整数分为两部分,分别处理两部分的情况(其实就是分类讨论)。
1.5几道经典的分块例题
(1) CF1207F Remainder Problem
思路:考虑对模数分块。设模数为\(P\),分两种情况:
- \(P\leq \sqrt N\)
此时,模\(P\)的结果一定小于\(\sqrt N\)。因此,我们只需要预处理出\(\mod P=y\)的位置的数之和,然后每次\(\Theta(1)\)查询即可。
预处理时间复杂度\(\Theta (N)\)。其中,枚举模数\(P\)时间复杂度\(\Theta(\sqrt N)\),枚举取模结果时间复杂度\(\Theta (\sqrt N)\)。
- \(P>\sqrt N\)
我们不能再通过预处理解决这种情况了。不难发现,如果设\(a_x \mod P = y\),这样的\(a_x\)一定不超过\(\sqrt N\)个。因此,我们只需要暴力对每个\(a_x\)进行查询或者修改即可。
(2)CF785E Anton and Permutation
思路:首先我们注意到,当交换两个数\(a_x, a_y(x<y)\)时,相对位置关系发生变化的只有区间\([x,y]\)。
也就是说,区间\([x,y]\)对该区间以外的区间逆序对个数的贡献是不变的。改变的是区间\([x,y]\)以内的区间的逆序对个数。
再来思考区间\([x,y]\)的逆序对个数是如何改变的。
将\(a_x\)移到\(y\)时,区间\((x,y]\)上,比\(a_x\)大的数都与移动后的\(a_x\)产生了逆序关系。
而区间\((x,y]\)上,比\(a_x\)小的数都与\(a_x\)解除了逆序关系。
所以\(a_x\)的移动所贡献的逆序对个数是:区间\([x,y]\)内,比\(a_x\)大的数的个数减去比\(a_x\)小的数的个数。
\(a_y\)也是同样的道理。
这样一来,我们需要一个数据结构,能够维护一个区间\([x,y]\)内,比\(a_x\)小的数的个数,比\(a_x\)大的数的个数。
考虑分块,用块内排序加上二分查找即可。每次查询时间复杂度:\(\Theta (\sqrt N\log_2 N)\).
(3)CF455D Serega and Fun
思路:区间向滚动实质上是将区间的最后面的一个元素切割下来,然后拼接到区间的最前面。
可以使用\(splay\)来维护这个区间。然而本题只需要将一个元素进行切割与拼接,\(splay\)显得大材小用了。
实际上我们可以考虑将区间直接分块。
首先考虑整块的滚动。整块的滚动十分简单,只要将块尾的元素直接切割下来拼到块头即可。可以用链表或者双端队列维护一个块。
如果一个区间包含了多个块,只需要将一个块的块尾切割,然后拼接到下一个块的块头即可。如果块长为\(T\),那么时间复杂度就是\(\Theta (\dfrac{N}{T})\)。
考虑没有被完全包含的块,暴力区间滚动即可。时间复杂度\(\Theta (T)\)。
当块长为\(\sqrt N\)时,理论时间复杂度最优。
(二)基于分块的离线算法——莫队
2.1 双指针法two pointers
先由这样一个问题引入:
"给定一个数组序列,和若干组询问。每次询问一个区间\([l,r]\)。问:在区间\([l,r]\)中,有多少种不同的数字。"
考虑使用双指针法。
用两个指针\(L,R\),一个指向区间的左端点,另一个指向区间的右端点。对于每次询问\([l,r]\),只需要不断移动\(L,R\)(每次移动一个单位),直到\(L,R\)刚好指向\(l,r\)。
因为每次\(L,R\)只移动一个单位,也就是说,每次最多只有一个新的元素加入到区间\([L, R]\)中。同时,每次最多只有一个元素从区间\([L,R]\)中删除。
我们只需要开一个\(cnt[x]\)数组记录再区间\([L,R]\)中\(x\)出现的次数。
如果在某次指针移动中,\(cnt[x]\)由\(1\)变成了\(0\),那么答案就要减\(1\)(数字的种类减少了\(1\))。
如果在某次指针移动中,\(cnt[x]\)由\(0\)变成了\(1\),那么答案就要加\(1\)(数字的种类增多了\(1\))。
对于每次询问这样做的时间复杂度为\(\Theta(N)\),因为左指针最多移动\(N\)次,右指针同样最多移动\(N\)次。
上述解法过于暴力,与直接统计区间\([l,r]\)的时间复杂度处在同一个量级(那我还不如直接统计)。一下是对双指针算法的优化。
优化
考虑离线处理。
将所有询问离线,然后按照询问的左端点排序。这样保证了左指针一定是向右移动的,且左指针最多移动\(N\)次。
然后再来看右指针的移动情况。右指针对于每个询问仍然最多要移动\(N\)次,当然这是在刻意构造数据的前提下。对于随机数据,右指针对于每个询问需要移动的次数远远小于\(N\)。
总的来看,如果设询问的个数为\(M\),那么时间复杂度就是\(\Theta(MN)\),看上去没怎么优化,实际上对于常数的优化还是蛮大的。
以上。(实际上优化没有这么少,以上章节是为了给莫队算法作铺垫)
2.2莫队算法
——利用分块大幅优化双指针法
相信各位都很好奇,分块如何优化双指针法呢?
还是先上一个问题。
例题1:CF576C Points on Plane
作为例题,简单讲一下题意。
给出平面上\(N\)个点的坐标\((x,y)\),求出这\(N\)个点的一个排列,使得所有相邻两点之间的曼哈顿距离之和小于等于\(2.5\times 10^9\)。
说人话:你要按照某种顺序走遍所有的点(这个顺序是\(N\)个点的某种排列),每次从一个点走到另一个点,花费的时间是两点之间的曼哈顿距离(即\(|x_1-x_2|+|y_1-y_2|\)),最后你走完所有点的总时间要小于等于\(2.5\times 10^9\)。求你走过点的顺序(不能重复走某一个点)。
举个例子,排列\(4,2,1,3\)就是从\(4\)号点走到\(2\)号点,再从\(2\)号点走到\(1\)号点,再从\(1\)号点走到\(3\)号点。
注意数据范围\(0\leq x_i,y_i,N\leq 10^6\)
以上是题意。
先别管这跟莫队有什么关系。考虑一下怎么安排顺序。
\(M\)表示横坐标或者纵坐标的最大差值。
方案一:随便走
可能有人已经笑了:这算什么方案。别急,先来分析一下距离。
首先,考虑最坏的情况。对于每个点可能要走\(2M\)个单位长度才能走到。一共有\(N\)个点,所以距离最大是\(2M\times N=2\times 10^{12}\)
(如果把\((x,y)\)当做区间\([l,r]\),这不就是双指针法按照顺序移动指针的复杂度吗)
方案二:将所有点按照\(x\)的大小排序
曼哈顿距离可分解为\(x\)轴方向的距离加上\(y\)轴方向的距离。
分析\(x\)轴方向上移动的距离:因为已经排好序了,所以在\(x\)轴方向上最多移动\(M\)个单位长度。
再来分析\(y\)轴方向上移动的距离:对于每个点,在纵方向上都有可能移动\(M\)个单位长度。因此在\(y\)轴方向上移动的最大距离为\(MN\)个单位长度。给一张图:

总距离为\(M + MN=10^6 +10^{12}\)不错,优化了上百万
(这不就是优化1将所有询问按照左端点排序然后离线处理的复杂度吗)
方案三:对\(x\)分块(分块大法好)
整个横坐标分为\(\sqrt M\)块,也就是分为\(1000\)块,每一块的长度为\(1000\),每一块最多有\(\sqrt N\)个横坐标不同的点。
每次移动按照块的顺序移动,也就是说,只能先将第一块的点都遍历了以后,才能去遍历第二块的点。
在每个块内,按照\(y\)的大小升序排列。
分析一下最大距离(每一块内):
\(x\)轴方向上:每次最大移动\(\sqrt M\)个单位长度,最多移动\(\sqrt N\)次。距离为\(\sqrt {MN}=10^6\)
\(y\)轴方向上:在每个块内最多移动\(M\)个单位长度。距离为\(M=10^6\)
总距离为\(\sqrt{MN}+M = 2\times 10^6\)
以上是每个块内最大的距离。再来算总距离。
\(x\)轴方向上,块与块之间最多移动\(\sqrt M\)个单位长度。
\(y\)轴方向上,块与块之间最多移动\(M\)(从上一个块最大的\(y\)移动到当前块最小的\(y\))。
块的数量为\(\sqrt M\),因此,总距离为\(\sqrt M\times (\sqrt{MN}+M+\sqrt M + M)=3\times 10^9 + 10^6\)
总距离得到了极大的优化,但还是超过了\(2.5\times 10^9\)
(将以上优化加入双指针法其实就是莫队了。下面的方案相当于莫队的优化。)
方案四:“玄学?”奇偶性排序
观察方案三,很容易发现,每次从上一个块的最大的\(y\)转移到当前块的最小的\(y\)实际上耗费很大的距离。
这让我们不禁想到,如果我们能从上一个块的最大的\(y\)转移到当前块最大的\(y\),那该多好。
其实,这很容易实现。只需要按照块的奇偶性确定\(y\)的排序方式即可。
比如说,第一块是奇数块,因此我们让第一块内的点按照\(y\)的升序排列。第二块是偶数块,因此我们让第二块内的点按照\(y\)的降序排列。以此类推。
这样一来,相邻两块之间的排序方式就不同,使得前一块最大的\(y\)能够对接上后一块最大的\(y\)。

不难证明,总距离就能稳定的消去一个\(M\),达到\(\sqrt M\times (\sqrt{MN}+\sqrt M +M)=2\times 10^9 + 10^6\)。终于在本题要求的范围以内了。
(上述优化其实就是对莫队普通排序的优化,网上很多题解都没有解释为什么莫队算法按照奇偶性排序能够起到很大的优化作用)
以上是例题讲解。
看完了例题,相信大家都已经对莫队算法有了自己的想法。下面是莫队算法的总结。
-
将询问按照左端点分块,每个块内按照右端点的大小排序(对应方案三)。
-
依次处理每个块内的询问,每次将指针\(L,R\)移动到询问区间\(l,r\)的位置。
优化: 排序时,按照块的奇偶性确定右端点是升序还是降序(对应方案四)。
代码实现:
sort(q+1, q+Q+1, cmp);//对询问的区间进行排序,分块
int l=1, r=0;//双指针
for(int i=1; i<=Q; i++){
int ql = q[i].l, qr = q[i].r;
while(l < ql) erase(a[l++]);//移动左端点
while(l > ql) insert(a[--l]);
while(r < qr) insert(a[++r]);//移动右端点
while(r > qr) erase(a[r--]);
ans[q[i].id] = now;//now是当前区间的答案
}
莫队主要是解决一些序列上的统计问题(诸如问有多少种不同的数字之类的)。
以上。
2.3时间复杂度分析
参考上一节方案三的分析过程:
设块长为\(T\),序列长度为\(N\)。
在一个块内:左端点的移动总距离最多为\(T^2\),右端点移动的总距离最多为\(N\)。
块与块之间的转移:左端点移动的次数最多为\(T\),右端点移动的次数最多为\(N\),转移的次数为\(\dfrac{N}{T}\)。
由于按照奇偶性排序,总复杂度可以消掉一个\(N\)。
总复杂度为\(\Theta(\dfrac{N}{T}(T^2 + T + N))=\Theta (NT+N+\dfrac{N^2}{T})\)
当且仅当\(T=\sqrt N\)时,理论时间复杂度最小,为\(\Theta(N\sqrt N)\)。
以上。
2.4几道经典的莫队例题
(1)CF86D Powerful array
板子题。
(2)CF617E XOR and Favorite Number
思路:根据套路,将区间异或转化为两点的异或。
设\(S_x=a_1\oplus a_2\oplus...\oplus a_{x-1}\oplus a_x\)
那么,\(a_l\oplus a_{l+1}\oplus ... \oplus a_{r-1}\oplus a_r=S_{l-1}\oplus S_r\)
问题就转化为了,在一段区间\([l-1, r]\)中,有多少对\(S_l,S_r\)满足\(S_l\oplus S_r=k\)。
根据异或的运算法则,上述等式可以变形为:\(S_l\oplus k=S_r\)。因此,开一个\(cnt\)数组统计当前区间的\(S_l\oplus k\),然后就是莫队的模板了。
2.5树上的莫队
既然莫队是序列上的算法,那么就有人将莫队搬到树上。
其实,大部分树上的问题都有一个固定的套路:即将树上的节点转化为连续的序列(区间),然后再套序列上的算法。
树上的节点转化为序列的常用方法是\(dfs\)序。由于莫队算法的特殊性(莫队算法的区间是要连续移动的,中途不能是跨越式地移动),决定了其不能像树链剖分那样使用\(dfs\)序转化。
常用的方法是使用欧拉序。所谓欧拉序,就是在深度优先遍历整棵树时,每个节点在第一次遍历时记录一次,在离开时再记录一次。
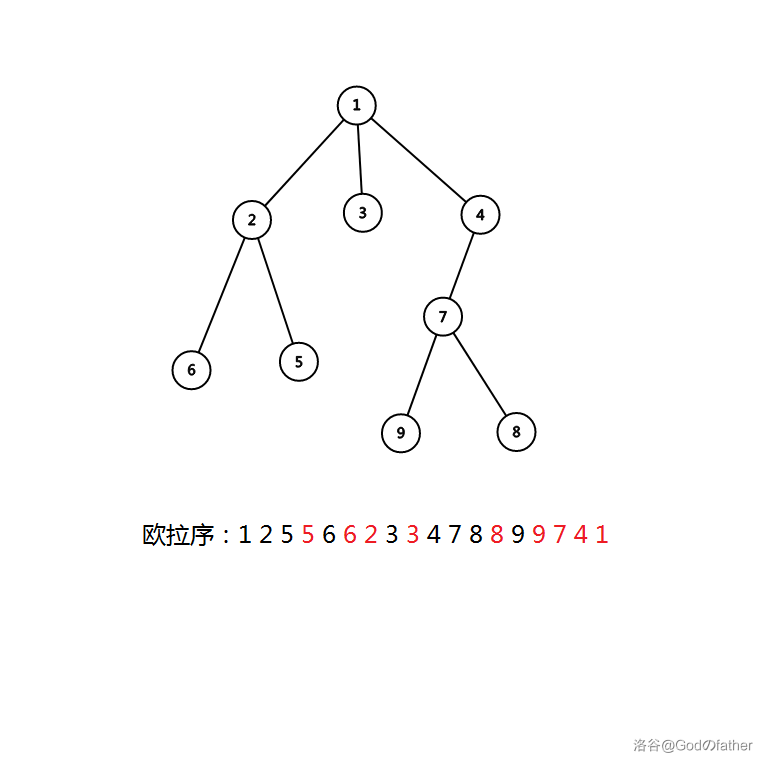
设树上路径的两个端点分别为\(x,y\)(\(x\)的深度小于\(y\)),设\(x\)在欧拉序列第一次出现的位置为\(\operatorname{first}(x)\),第二次出现的位置为\(\operatorname{second}(x)\)。
根据结合欧拉序的性质,容易发现对于树上两点间的路径可以分为两类:
- \(x\)是\(y\)的祖先(即\(x=\operatorname{lca}(x,y)\))
路径上的节点就是欧拉序上\(\operatorname{first}(x)\)到\(\operatorname{second}(y)\)之间所有只出现过一次的节点。
- \(x\)不是\(y\)的祖先(即\(\operatorname{lca}(x,y)\)在\(x,y\)的路径上)
这个路径可以分为两个部分。
第一个部分是从\(x\to \operatorname{lca}(x,y)\)。这一部分包含的节点可以用1中的结论求出。
第二个部分是从\(\operatorname{lca}(x,y)\to y\)。这一部分包含的节点同样可以用1中的节点求出。
将上面两个部分合二为一,就变为了从\(\operatorname{second}(x)\)到\(\operatorname{first}(y)\)上只出现过一次的节点,再加上\(\operatorname{lca}(x,y)\)即可。
以上为树上的路径转化为序列上的区间的方法。
如此,树上问题就被我们搬到区间上了,只需要每次移动指针,对于出现第二次的节点执行删除操作,对于第一次出现的节点执行加入操作即可。
一道例题:CF852I Dating
同样是树上莫队的模板。附上代码(不要在意\(longlong\)):
#include<bits/stdc++.h>
using namespace std;
const long long maxn = 1e5 + 5;
inline long long read(){
long long x=0ll,f=1ll;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') f=-1ll;ch=getchar();}
while (isdigit(ch)){x=x*10ll+ch-48ll;ch=getchar();}
return x*f;
}
long long head[maxn], Next[maxn<<1], ver[maxn<<1], tot;
void add(long long x, long long y){
ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}
long long sex[maxn], num[maxn], N, Q;
long long f[maxn], son[maxn], siz[maxn], d[maxn], id[maxn], top[maxn], cnt;
pair<int, int> a[maxn];
struct node{
long long l, r, id, lca;
}q[maxn];
long long belong[maxn<<1], first[maxn], last[maxn], dfn, seq[maxn<<1], ans[maxn], now;
long long times[2][maxn], vis[maxn];
void dfs1(long long x, long long fa, long long deep){//树链剖分求lca
f[x] = fa, siz[x] = 1, seq[++dfn] = x, first[x] = dfn, d[x] = deep;
for(long long i=head[x]; i; i=Next[i]){
long long y = ver[i];
if(y == fa) continue;
dfs1(y, x, deep + 1);
siz[x] += siz[y];
if(siz[y] > siz[son[x]] or son[x] == 0) son[x] = y;
}
seq[++dfn] = x, last[x] = dfn;
}
void dfs2(long long x, long long TOP){
top[x] = TOP;
if(!son[x]) return ;
dfs2(son[x], TOP);
for(long long i=head[x]; i; i=Next[i]){
long long y = ver[i];
if(y == f[x] or y == son[x]) continue;
dfs2(y, y);
}
}
long long lca(long long x, long long y){
while(top[x] != top[y]){
if(d[top[x]] < d[top[y]]) swap(x, y);
x = f[top[x]];
}
if(d[x] > d[y]) swap(x, y);
return x;
}
bool cmp(node x, node y){
if(belong[x.l] == belong[y.l]){
if(belong[x.l]&1) return x.r < y.r;
else return x.r > y.r;
}
return belong[x.l] < belong[y.l];
}
void update(long long x){
if(vis[x]) now -= times[sex[x]^1][num[x]], times[sex[x]][num[x]] --;//第二次出现的节点删除
else now += times[sex[x]^1][num[x]], times[sex[x]][num[x]] ++;//第一次出现的节点加入
vis[x] ^= 1;//记录当前节点是否是第一次出现
}
int main(){
N = read();
for(long long i=1; i<=N; i++) sex[i] = read();
for(long long i=1; i<=N; i++) num[i] = read(), a[i] = make_pair(num[i], i);
sort(a+1, a+N+1);
long long rk = 0;
for(long long i=1; i<=N; i++){
if(a[i].first != a[i-1].first or i == 1) rk ++;
num[a[i].second] = rk;
}
for(long long i=1; i<N; i++){
long long x, y;
x = read(), y = read();
add(x, y); add(y, x);
}
dfs1(1, 0, 1);//树链剖分求lca
dfs2(1, 1);
long long len = sqrt(dfn), bnum = ceil((double)dfn/len);
for(long long i=1; i<=bnum; i++){
for(long long j=len*(i-1) + 1; j<=min(len*i, dfn); j++)
belong[j] = i;
}
Q = read();
for(long long i=1; i<=Q; i++){
long long x, y;
x = read(), y = read();
if(first[x] > first[y]) swap(x, y);
long long LCA = lca(x, y);
if(x == LCA){
q[i].l = first[x], q[i].r = first[y];
}
else{
q[i].l = last[x], q[i].r = first[y];
q[i].lca = LCA;
}
q[i].id = i;
}
sort(q+1, q+Q+1, cmp);
long long l = 1, r = 0;//以下是莫队模板
for(long long i=1; i<=Q; i++){
long long ql = q[i].l, qr = q[i].r;
while(l > ql) update(seq[--l]);
while(l < ql) update(seq[l++]);
while(r < qr) update(seq[++r]);
while(r > qr) update(seq[r--]);
if(q[i].lca) update(q[i].lca);//对于第二种情况要加上lca
ans[q[i].id] = now;
if(q[i].lca) update(q[i].lca);
}
for(long long i=1; i<=Q; i++) printf("%lld\n", ans[i]);
return 0;
}
以上。
2.6带修改的莫队
莫队作为一个离线算法,自然不支持在线修改。莫队的修改也是离线做的。
带修改的莫队实际上可以看成多了一维的莫队。由于每次修改后整个序列都会被改变,因此我们要记录每个询问前被修改的次数。
如果我们还是按照普通莫队那样排序的话,每个块内的修改次数并不是连续的。这样就产生了一个问题:上一个询问是修改了\(10\)次的序列中,下一个询问却只是在修改了\(5\)次的序列中,我们就需要把\(10\)次修改还原为\(5\)次修改。
容易看出,上述做法就像在无序的情况下的双指针法,做了很多无用功。所以,我们也要将修改次数\(k\)按照升序排列。
做法就是在左端点的每一块内,将右端点分块,再在右端点的块内将\(k\)升序排列。
这个排序方式同样可以使用奇偶性排序优化。
总而言之,带修改的莫队仅仅是比一般的莫队多了一维,修改一下排序方式,再加一个指针即可(可以看作三维莫队)。
三维莫队时间复杂度分析
网上很多博客都有提到三维莫队分块的大小为\(N^{\frac{2}{3}}\)时理论复杂度最优,却没有具体分析。以下分析忽略常数。
设分块大小为\(T\),序列长度为\(N\),修改次数为\(M\)。
时间复杂度主要在三个指针的移动上面。
左指针移动的复杂度为\(\Theta (NT)\)
在同一块左指针内,右指针移动的复杂度为\(\Theta(T^2+N)\)
右指针移动的总时间复杂度为\(\Theta(NT+\dfrac{N^2}{T})\)
在同一块左指针内,在同一块右指针内,k指针的移动复杂度为\(\Theta(M)\)
在同一块左指针内,k指针移动的复杂度为\(\Theta (\min \{ MT,\dfrac{MN}{T}\})\)
k指针移动的总复杂度为\(\Theta(\min\{MN,\dfrac{N^2M}{T^2}\})=\Theta (\dfrac{N^2M}{T^2})\)
当\(T=\sqrt[3] {NM}\),上述三个函数取得最小值。时间复杂度为\(\Theta(\sqrt[3]{N^4M})\)
以上。
一道例题:CF940F Machine Learning
板子题。直接上代码。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 15;
int N, Q, a[maxn], askM, changeM, belong[maxn], cnt[maxn<<1], st[maxn], ans[maxn], b[maxn<<1], tot;
struct node{
int l, r, id, k;
}ask[maxn];
struct NODE{
int x, y;
}change[maxn];
bool cmp(node x, node y){
if(belong[x.l] == belong[y.l]){
if(belong[x.r] == belong[y.r]){
if(belong[x.r]&1) return x.k < y.k;
else return x.k > y.k;
}
if(belong[x.l]&1) return belong[x.r] < belong[y.r];
return belong[x.r] > belong[y.r];
}
return belong[x.l] < belong[y.l];
}
void del(int x){
st[cnt[x]] --;
cnt[x] --;
st[cnt[x]] ++;
}
void ins(int x){
st[cnt[x]] --;
cnt[x] ++;
st[cnt[x]] ++;
}
int main(){
scanf("%d%d", &N, &Q);
for(int i=1; i<=N; i++) scanf("%d", &a[i]), b[++tot] = a[i];
for(int i=1; i<=Q; i++){
int opt, l, r, x, y;
scanf("%d", &opt);
if(opt == 1){
scanf("%d%d", &l, &r); askM ++;
ask[askM].l = l, ask[askM].r = r, ask[askM].id = askM, ask[askM].k = changeM;
}
else{
scanf("%d%d", &x, &y); changeM ++;
change[changeM].x = x, change[changeM].y = y, b[++tot] = y;
}
}
sort(b+1, b+tot+1);
tot = unique(b+1, b+tot+1) - b;
for(int i=1; i<=N; i++) a[i] = lower_bound(b+1, b+tot+1, a[i]) - b;
for(int i=1; i<=changeM; i++) change[i].y = lower_bound(b+1, b+tot+1, change[i].y) - b;
int len = pow(N, (double)2.0/3.0), bnum = ceil((double)N/len);
for(int i=1; i<=bnum; i++)
for(int j=(i-1)*len + 1; j<=min(i*len, N); j++) belong[j] = i;
sort(ask+1, ask + askM + 1, cmp);
int l = 1, r = 0, time = 0;
for(int i=1; i<=askM; i++){
int ql = ask[i].l, qr = ask[i].r, qt = ask[i].k;
while(l > ql) ins(a[--l]);
while(l < ql) del(a[l++]);
while(r < qr) ins(a[++r]);
while(r > qr) del(a[r--]);
while(time < qt){
time ++;
if(l <= change[time].x and change[time].x <= r) del(a[change[time].x]), ins(change[time].y);
swap(a[change[time].x], change[time].y);
}
while(time > qt){
if(l <= change[time].x and change[time].x <= r) del(a[change[time].x]), ins(change[time].y);
swap(a[change[time].x], change[time].y);
time --;
}
int now = 0;
while(st[now+1]) now ++;
ans[ask[i].id] = now+1;
}
for(int i=1; i<=askM; i++) printf("%d\n", ans[i]);
return 0;
}
附:奇偶性排序优化的效果

以上。
(三)后记
没什么好说的。写这么长一篇文章真的挺累。
祝:有所收获。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号