[网络流24题]P1251 餐巾计划

最大流好题！构造，思维
https://www.luogu.com.cn/problem/P1251

这个建模真的是很好的构造，凹了半天

Tutorial

不难想到把点拆成早上：输出干净毛巾，晚上：输出脏毛巾
一开始有一个很符合直觉的想法，大概建成这个样子

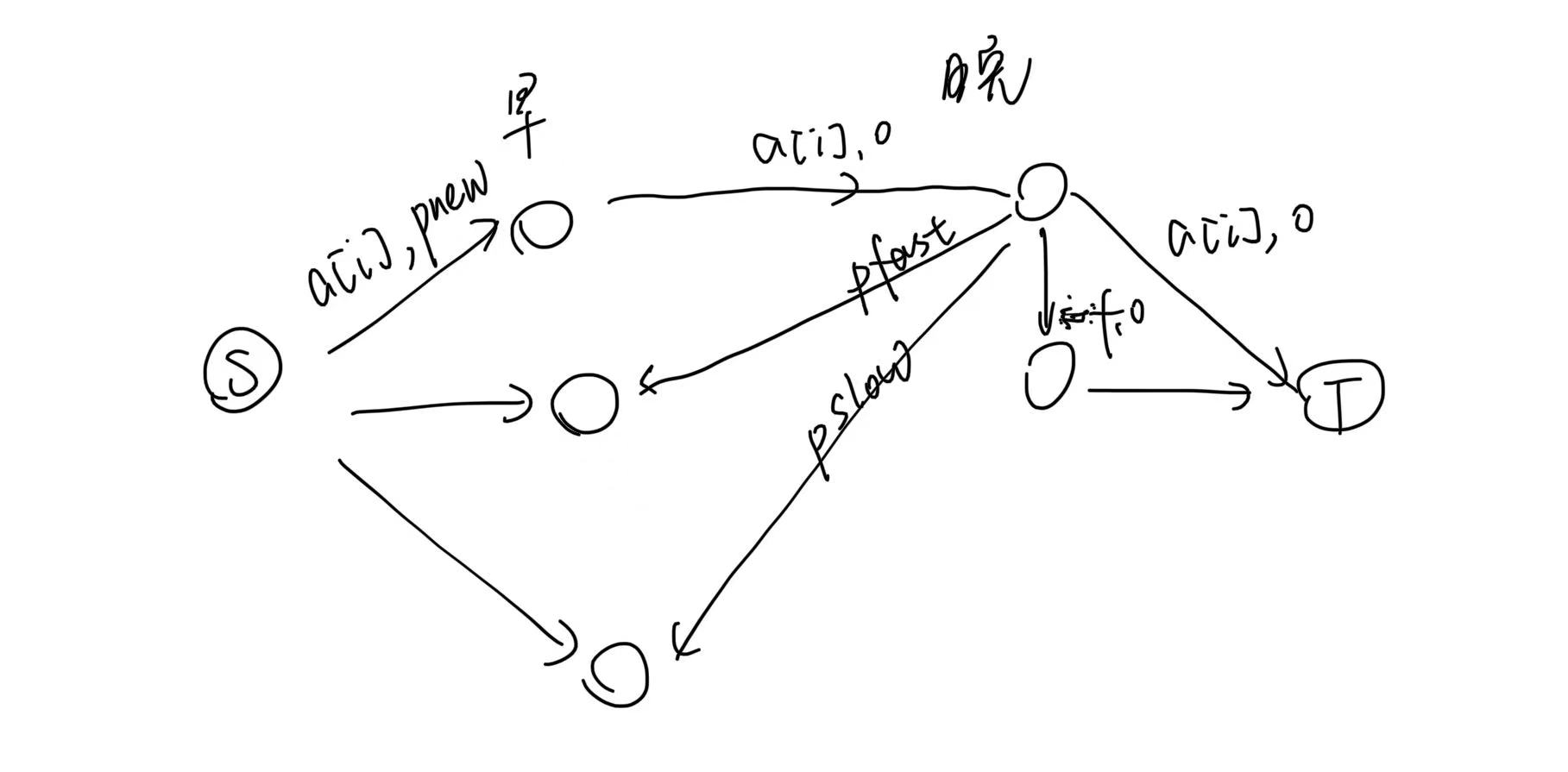
不难发现这样有一个问题，这样每条毛巾的最短路长度都是直接购买，这显然是没有限制住题目条件。然后不妨考虑考虑让只有第一个点买毛巾，反正是要让一些点不需要走那条长度为pnew的路，期间画出了这样的东西orz

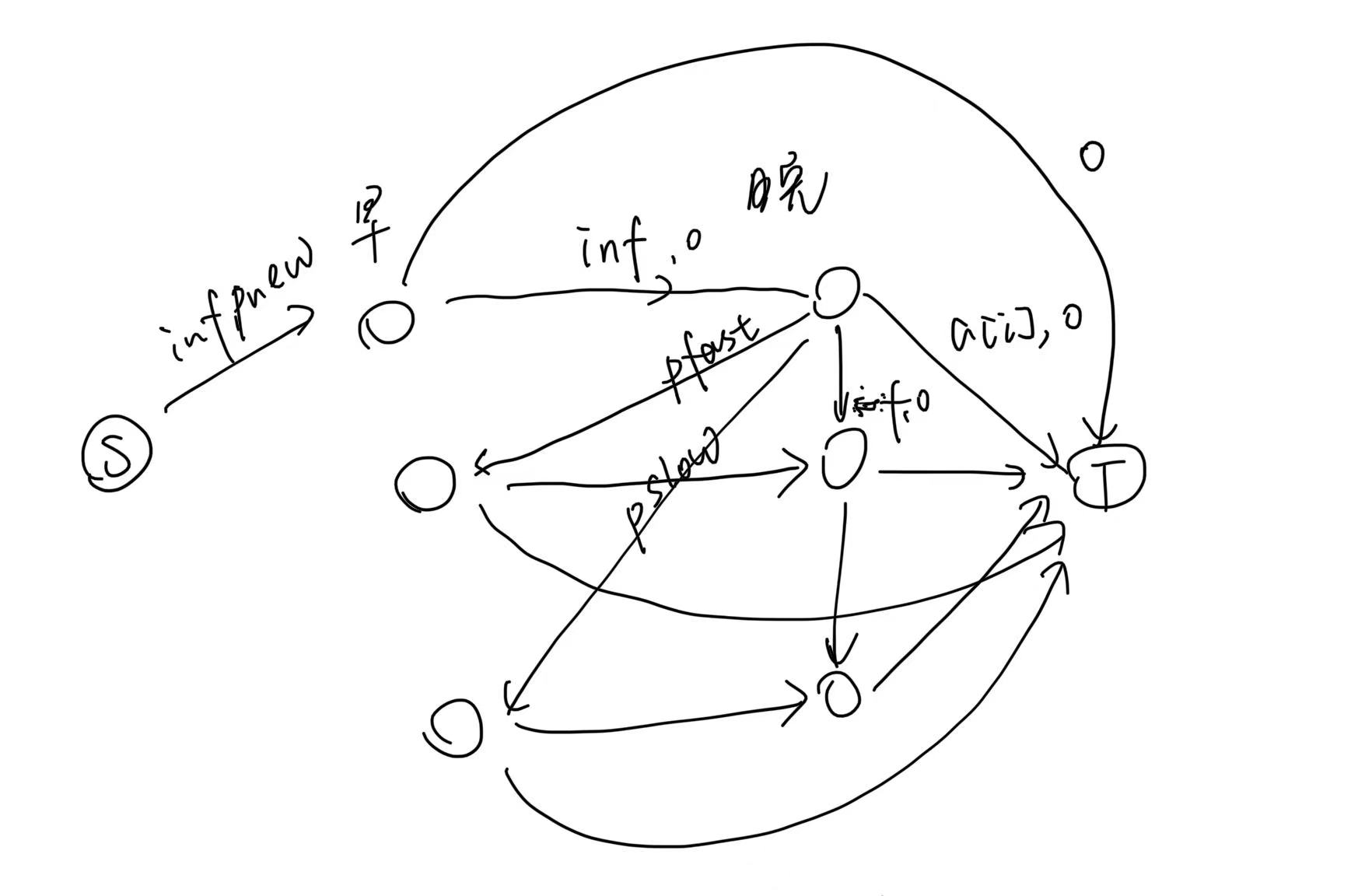
然后想到，既然每个晚上会自然得到当天用过的 \(a[i]\) 个脏毛巾，那么不妨直接让 \(S\) 连晚上的点，这样距离就是 \(0\) 了。晚上的脏毛巾来源有 白天用的（\(S\)连过来），前面的白天用了没洗的，去向可以不洗去下一天晚上，或者花费 \(pfast/pslow\) 送到相应的白天的点。
对于白天的点，\(a[i]\) 连汇点表示每天开始要有足够的干净毛巾，最大流保证一定流满。来源有买的(从源点买)，洗的
综上所以只需要连下面6种边

addflow(S, id(i, 0), inf, pnew);//买毛巾
addflow(S, id(i, 1), a[i], 0);//当天产生的脏毛巾
addflow(id(i, 0), T, a[i], 0);//当天使用的干净毛巾
if (i + dfast <= n) addflow(id(i, 1), id(i + dfast, 0), inf, pfast);//快洗
if (i + dslow <= n) addflow(id(i, 1), id(i + dslow, 0), inf, pslow);//慢洗
if (i < n) {
    addflow(id(i, 1), id(i + 1, 1), inf, 0);//不洗，堆到下一天处理
}

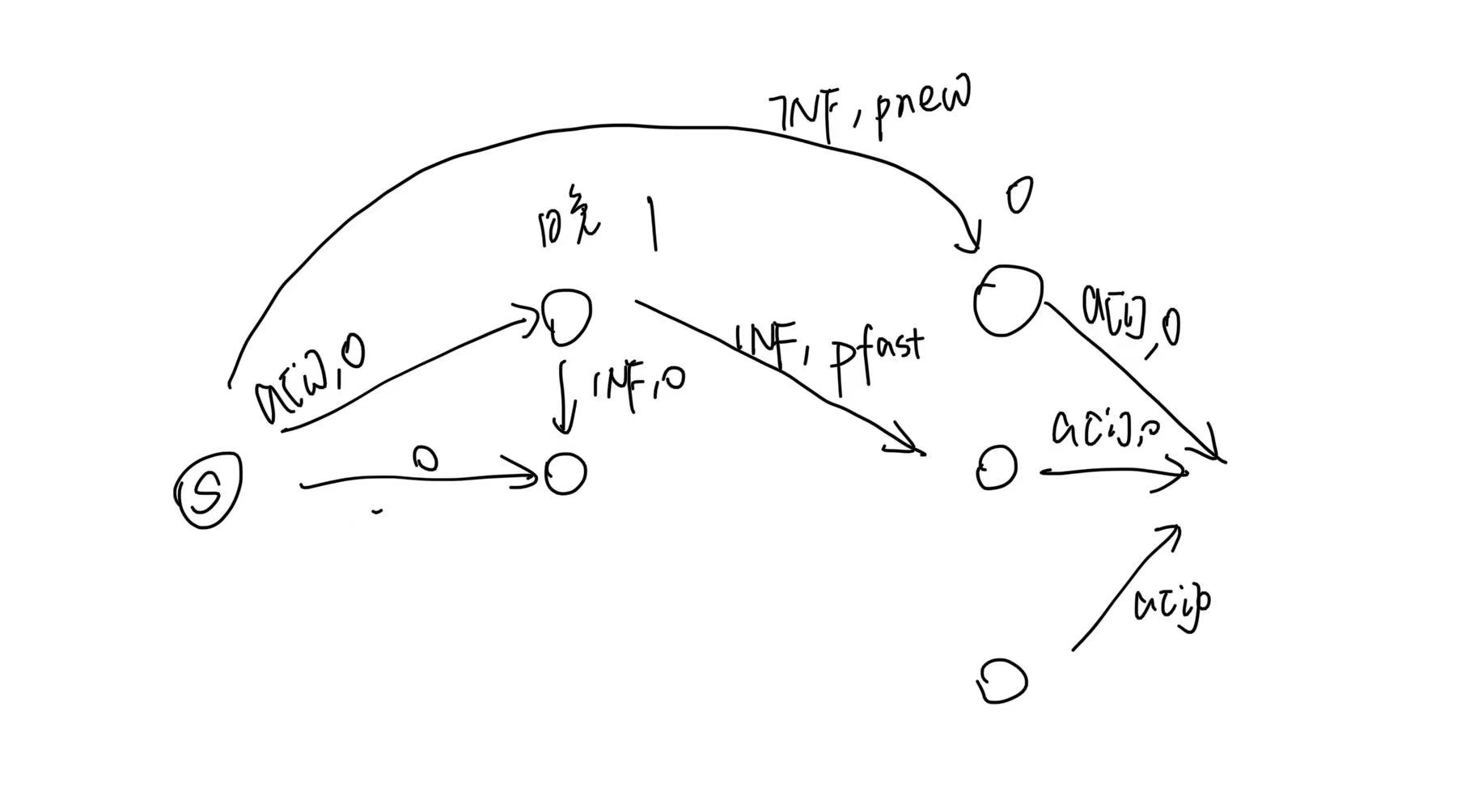
此处有一细节，因为毛巾可以堆着不洗，所以所有洗衣服，堆衣服的边容量都应该为 \(INF\)，不能忽略前面点的影响

点击查看代码

#include <bits/stdc++.h>
#define endl '\n'
#define IOS                  \
    ios::sync_with_stdio(0); \
    cin.tie(0);              \
    cout.tie(0)
#define P pair<int, int>
typedef long long ll;
using namespace std;

const int maxn = 2 * 2000 + 5;
const ll inf = 1e18;
const int INF = 0x3f3f3f3f;
int n, cnt_edge = 1, S, T;
int a1[maxn], a2[maxn], head[maxn];
ll dis[maxn];
bool vis[maxn];
struct edge {
    int to, nxt;
    ll flow, cost;
} e[(maxn * maxn) << 2];
inline void add(int u, int v, ll w, ll c) {
    e[++cnt_edge].nxt = head[u];
    head[u] = cnt_edge;
    e[cnt_edge].to = v;
    e[cnt_edge].flow = w;
    e[cnt_edge].cost = c;
}
/*u,v,flow,cost*/
inline void addflow(int u, int v, ll w, ll c) {
    add(u, v, w, c);
    add(v, u, 0, -c);
}
inline bool spfa(int on) {
    memset(vis, 0, sizeof(vis));
    if (on == 1)
        for (int i = 0; i <= T; i++) dis[i] = inf;
    else
        for (int i = 0; i <= T; i++) dis[i] = -inf;

    queue<int> q;
    q.push(S);
    dis[S] = 0;
    vis[S] = 1;
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        vis[x] = 0;
        for (int i = head[x]; i; i = e[i].nxt) {
            int y = e[i].to;
            // cout << "->" << y << endl;
            if ((on == 1 && e[i].flow && dis[y] > dis[x] + e[i].cost) ||
                (on == -1 && e[i].flow && dis[y] < dis[x] + e[i].cost)) {
                dis[y] = dis[x] + e[i].cost;
                if (!vis[y]) q.push(y), vis[y] = 1;
            }
        }
    }
    // cout << dis[T] << endl;
    if (on == 1)
        return dis[T] != inf;
    else
        return dis[T] != -inf;
}
ll dfs(int x, ll lim) {
    vis[x] = 1;
    if (x == T || lim <= 0) return lim;
    ll res = lim;
    for (int i = head[x]; i; i = e[i].nxt) {
        int y = e[i].to;
        if (dis[y] != dis[x] + e[i].cost || e[i].flow <= 0 || vis[y]) continue;
        ll tmp = dfs(y, min(res, e[i].flow));
        res -= tmp;
        e[i].flow -= tmp;
        e[i ^ 1].flow += tmp;
        if (res <= 0) break;
    }
    return lim - res;
}
/*on == 1时为最小费用，on == -1为最大费用*/
inline ll Dinic(int on) {
    ll res = 0, cost = 0;
    while (spfa(on)) {
        ll flow = dfs(S, inf);
        res += flow, cost += flow * dis[T];
    }
    return cost;
}
int id(int x, int on) { return n * on + x; }
int a[maxn], pnew, pfast, dfast, pslow, dslow;
int main() {
    cin >> n;
    S = n + n + 1, T = S + 1;
    for (int i = 1; i <= n; i++) cin >> a[i];
    cin >> pnew >> dfast >> pfast >> dslow >> pslow;

    for (int i = 1; i <= n; i++) {
        addflow(S, id(i, 0), inf, pnew);
        addflow(S, id(i, 1), a[i], 0);
        addflow(id(i, 0), T, a[i], 0);
        if (i + dfast <= n) addflow(id(i, 1), id(i + dfast, 0), inf, pfast);
        if (i + dslow <= n) addflow(id(i, 1), id(i + dslow, 0), inf, pslow);
        if (i < n) {
            addflow(id(i, 1), id(i + 1, 1), inf, 0);
        }
    }

    cout << Dinic(1) << endl;
    return 0;
}