[网络流24题]P2765 魔术球问题

拆点好题，边增广边求解
https://www.luogu.com.cn/problem/P2765

题意

给 \(n\) 个柱子，有一些值为 \(1,2,\dots,num\) 的球，要求每个球放在柱子上相邻的球必须和为平方数，问 \(n\) 个柱子最多能放多少球

题解

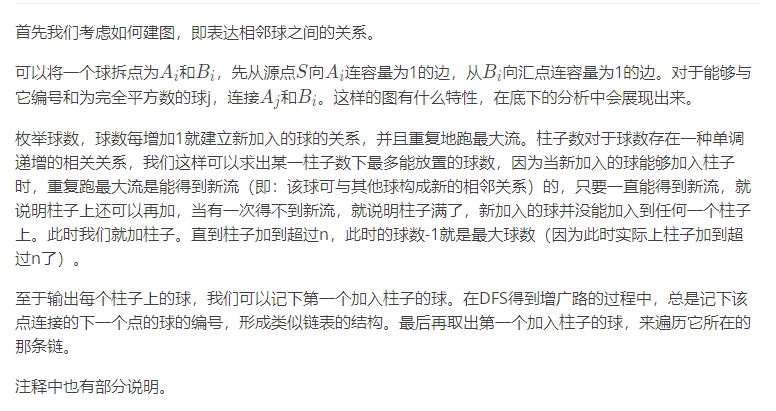
上图来自https://ksmeow.moe/graph_flow_24prob_sol/

而我的理解是一个球左边最多和一个球相连，右边最多和一个球相连，这和匹配问题十分相似。这样就是求一个最大匹配~这也决定了这题的拆点和普通的拆点表示的意义是不太一样的

点击查看代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
const int M = N;
const int INF = 0x3f3f3f3f;

struct edge {
    int v, w, to;
} e[M * 2];
int pre[N << 1], cnt_edge, dep[N << 1];
int S, T, z, head[N << 1], sum;
int n, m, q[N << 1], cur[N << 1];
void add(int u, int v, int w) {
    // cout << u << " " << v << " " << cnt_edge << endl;
    e[cnt_edge] = {v, w, head[u]};
    head[u] = cnt_edge++;
    e[cnt_edge] = {u, 0, head[v]};
    head[v] = cnt_edge++;
}
bool bfs() {
    for (int i = 0; i <= T; i++)
        dep[i] = 0;
    dep[S] = 1;
    int l = 0, r = 1;
    q[r] = S;
    while (l < r) {
        int u = q[++l];
        for (int i = head[u]; i != -1; i = e[i].to) {
            int v = e[i].v;
            if (!dep[v] && e[i].w)
                dep[v] = dep[u] + 1, q[++r] = v;
        }
    }
    return dep[T];
}
int dfs(int u, int mi) {
    int res = 0;
    if (mi == 0 || u == T)
        return mi;
    for (int& i = cur[u]; i != -1; i = e[i].to) {
        int v = e[i].v;
        if (dep[u] + 1 == dep[v] && e[i].w) {
            int minn = dfs(v, min(mi - res, e[i].w));
            e[i].w -= minn;
            e[i ^ 1].w += minn;
            if (minn > 0)
                pre[u / 2] = v / 2;
            res += minn;
            if (res == mi)
                return res;
        }
    }
    if (res == 0)
        dep[u] = 0;
    return res;
}
int dinic() {
    ll res = 0;
    while (bfs()) {
        memcpy(cur, head, sizeof(head));
        //    cout<<res<<endl;
        res += dfs(S, INF);
    }
    return res;
}
bool isssqu(int n) {
    int x = sqrt(n);
    return x * x == n;
}
int id(int x, int y) {
    return 2 * x + y;
}
bool vis[N];
int ans[N];
int main() {
    memset(head, -1, sizeof head);
    S = N - 4, T = S + 1;
    int pillar = 0, now = 0;
    cin >> n;
    while (pillar <= n) {
        now++;
        add(S, id(now, 0), 1);
        add(id(now, 1), T, 1);
        for (int i = sqrt(now) + 1; i * i < (now << 1); i++) {
            add(id(i * i - now, 0), id(now, 1), 1);
        }
        int flow = dinic();
        if (!flow) {
            ans[++pillar] = now;
        }
    }
    cout << now - 1 << endl;
    // for(int i =1;i<=now;i++) cout<<ans[i]<<" \n"[i == now];
    for (int i = 1; i <= n; i++) {
        if (!vis[ans[i]]) {
            for (int u = ans[i]; u != 0 && u != (T >> 1); u = pre[u]) {
                vis[u] = true;
                cout << u << " ";
            }
            cout << endl;
        }
    }
    return 0;
}