论文阅读 | Q-Transformer

0 摘要

  • 适用对象：离线数据集和演示数据支持的多任务策略场景

  • 使用Transformer作为Q-function估计的可扩展的展示

  • 离散化动作空间维度，将每一个动作维度的Q-值表示为独立的token

  • Q-Transformer表现超过了离线RL算法和模仿学习

  • 感觉像是对DT的改进，前者停留在宏观层面

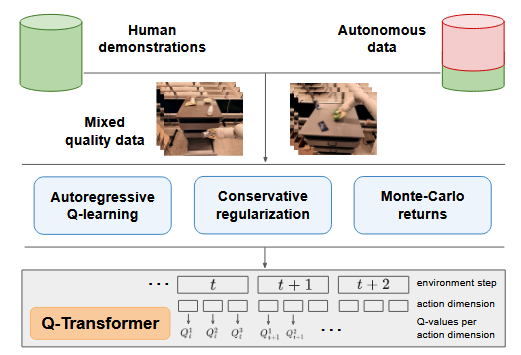
1 Introduction

  • 许多机器人领域高容量模型采用SFT训练，导致模型存在缺陷：(1)机器人系统不能超越人工的熟练水平；(2)机器人系统不能通过采集的经验变得更好，只能依赖高质量的演示。
  • 研究目标：将基于多样的现实数据集学习的大规模机器人学习与吸纳到高容量的基于Transformer模型的策略架构结合起来。
  • high-capacity model只要在基于大规模和多样化的数据集上训练才有意义，专而小的数据集并不需要这样的容量且不会获益。
  • offline RL dataset包括高质量的演示轨迹和模仿学习产生的次优轨迹
  • offline RL:代表CQL
    • 本文目标不是为离线 RL 开发一种新的算法原理，而是设计一个可以与大容量 Transformer 集成的离线 RL 系统，并扩展到现实世界的多任务机器人学习。
    • 使用了CQL的改进版
  • Tranformer-based 架构：
    • 大部分Tranformer-based 架构使用SFT，少部分使用Tranformer for RL和条件模仿学习
    • DT：将条件模仿学习与奖励条件反射扩展为使用序列模型。尽管 DT 融合了 RL 的元素（即奖励函数），但它并没有提供一种机制来改进已演示的行为或重新组合数据集的各个部分以合成更优化的行为，并且确实已知存在理论局限性 [63]。另一方面，这种基于模仿的 recipes 很受欢迎，可能是因为难以将 Transformer 架构与更强大的时间差分方法（例如 Q-learning）集成。
    • Q-Learning DT:提议将 Q-function 与基于 Transformer 的策略结合使用，但 Q-function 本身并没有使用基于Transformer 的架构.(但Q-Transformer重点在于直接训练 Transformer 来表示 Q 值)

3 Background

  • 离线数据集是按照某个未知的策略\(\pi_{\beta}\)产生的轨迹。这对现实世界的robotic learning比较有意义，因为on-policy data采集是非常耗时间的。
  • 应对分布偏移：添加保守惩罚(Conservative Penalty),将数据集之外的任何动作的Q值\(Q(s,a)\)下推，从而确保最大值动作在分布内。
  • 奖励函数设计：按照机器人界常见设置，采用稀疏奖励，设置二进制奖励R\(\in\){0,1}，1代表胜利完成任务，在episode的结尾出现。

4 Q-Transformer

整体架构：

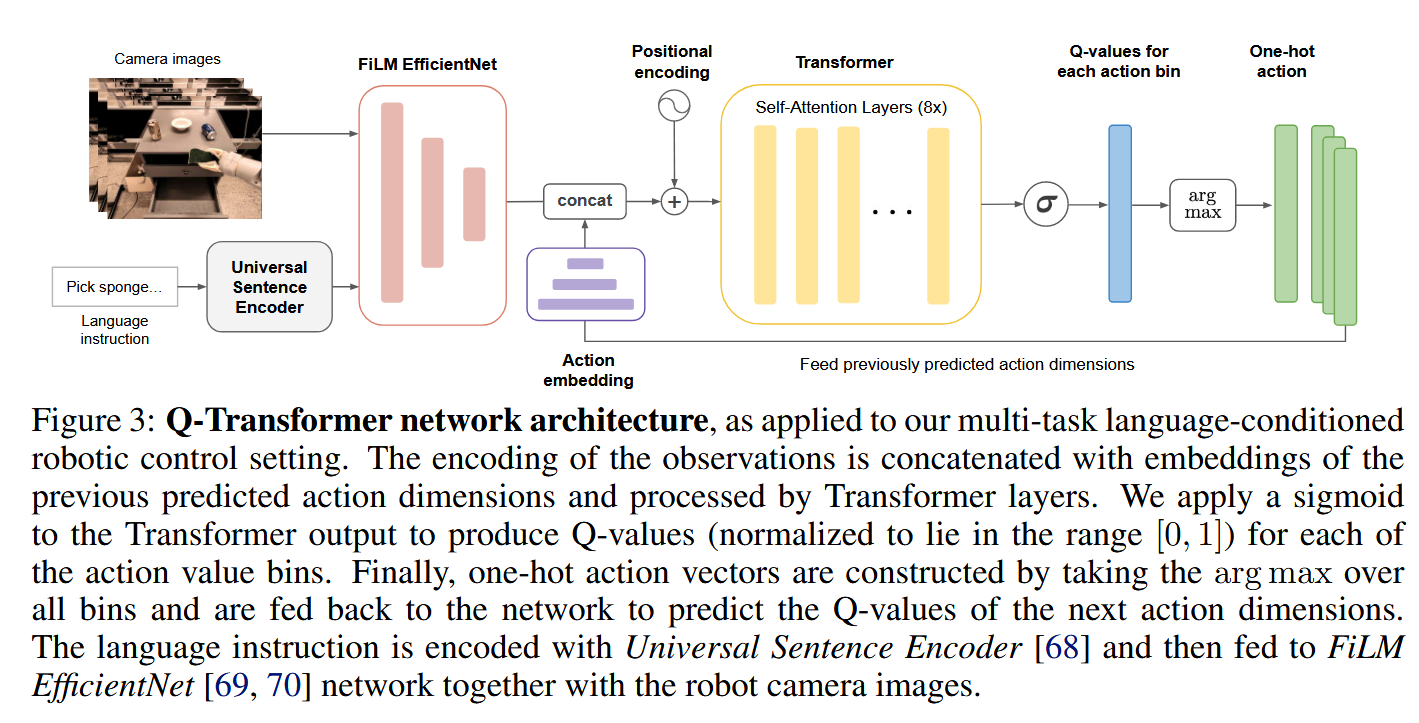
三个部分

4.1 Autoregressive Discrete Q-Learning

  • 使用Transformer with Q-Learning的两个挑战：
    • 要求离散化动作空间
    • 在离散化动作上进行Q值最大化，同时避免维度的干扰
  • 设计核心：将每一个动作维度作为一个独立的时间步
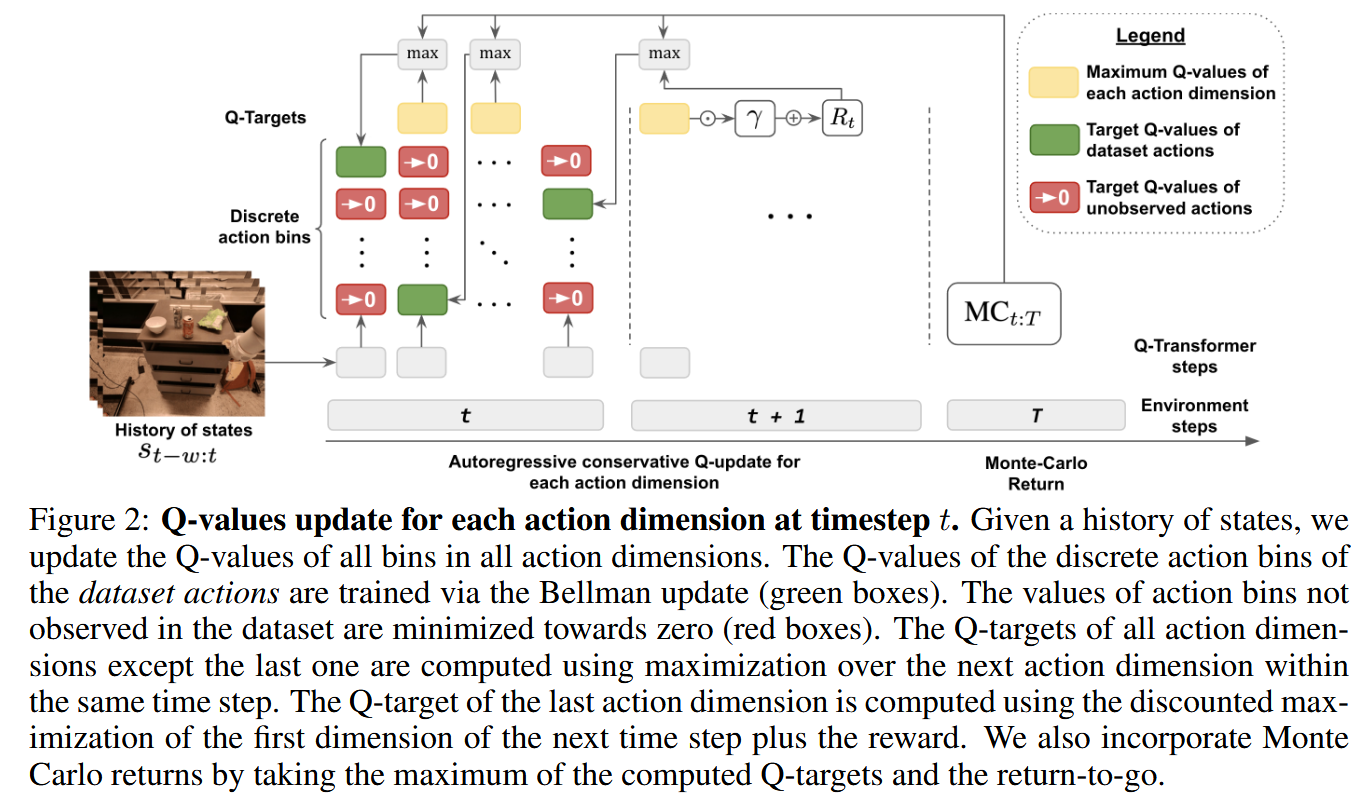
  • 需要注意的是，通过将每个动作维度视为贝尔曼更新的时间步骤，我们并未改变Q学习算法的整体优化特性。对于给定的马尔可夫决策过程（MDP），由于我们在假设未来所有动作维度均已达到最优的前提下对当前动作维度进行最大化操作，贝尔曼最优性原理仍然成立。证明详见附录A和B

4.2 Conservative Q-Learning with Transformers

  • 目标问题：需要解决由于分布偏移导致的过高估计问题，这种情况发生在目标值的Q函数在不同于其训练时所使用的动作上进行查询时
  • CQL： 最小化了分布外动作的 Q 函数，这可能导致 Q 值明显小于在任何轨迹中可以获得的最小可能累积奖励。尤其在稀疏奖励下可能出现不正常选择
  • 改进CQL：与其最小化数据中未出现动作的Q值，不如将这些Q值正则化，使其接近可能获得的最小累积奖励=\(R_{min}T\),在实验环境下为0

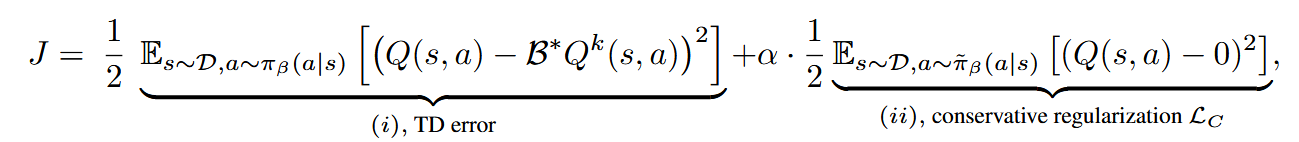
4.3 Improving Learning Efficiency with Monte Carlo and n-step Returns

  • 理论依据：数据集包含好的轨迹和次优的轨迹。使用蒙特卡洛 return to go 估计可以加速Q-Learning提示性能，因为MC沿着好的轨迹估计可以更快的value 传播
  • 使用最优Qvalue的下界-蒙特卡洛估计以加速贝尔曼更新：已知\(Q*(s_t,a_t)\geq MC_{t:T}=\sum^{T}_{j=t}\gamma^{j-t}R(s_j.a_j)\)，因此Bellman update:max(\(MC_{t:T},Q(s_t,a_t)\))
  • 对上面MC加速学习的原因解释：在实践中，首先学习最终时间步 (sT​,aT​) 的Q值，然后在未来的梯度步骤中向后传播。Q值可能需要经过多次梯度更新才能完全传播到 (s1​,a1​)。使用 max(MC,Q) 可以在训练开始时，即在Q值完全传播之前，对 Q(s1​,a1​) 应用有用的梯度。
  • n-step Returns：a little trick，准确率影响极小但训练速度极大提高。选择n-steps over action dimension使得下一个时间步的最后一个维度的final Q value被用作Q-target

5 实验

  • 实验目的：
    -（1） Q-Transformer 能否从演示和次优数据的组合中学习？
    -（2） Q-Transformer 与其他方法相比如何？
    -（3） Q-Transformer 中的具体设计选择有多重要？
    -（4） QTransformer 可以应用于大规模现实世界的机器人作问题吗

5.1 Real-world language-conditioned manipulation evaluation

  • 训练数据集：实验中使用的离线数据是由 13 个机器人组成的车队收集的，由 Brohan 等人 描述的演示数据的子集以及较低质量的自主收集的数据组成。这些演示是通过人工远程作收集的，用于 700 多个不同的任务，每个任务都有单独的语言描述。我们每个任务最多使用 100 个演示，总共约 38000 个演示。所有这些演示都成功完成了各自的任务并获得 1.0 的奖励。数据集的其余部分是通过自主运行机器人来收集的，执行通过行为克隆学习的策略。大约 20,000 个额外的自主收集的失败事件，每个事件的奖励为 0.0，数据集大小约为 58,000 个事件。episode的平均长度为 35 个时间步长。
    Real world manipulation tasks
    任务描述：例如“抽屉拾取和放置”、“打开和关闭抽屉”、“将对象移动到目标附近”
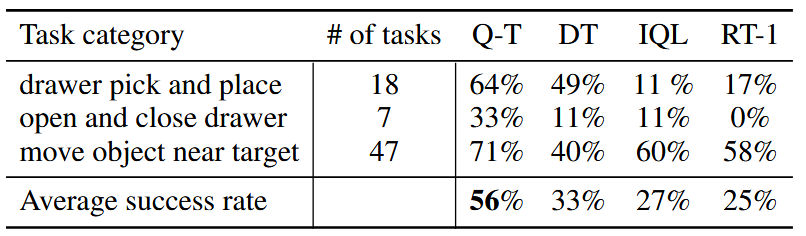
    Real world performance comparison
    这表明 Q-Transformer 可以有效地改进使用自主收集的次优数据的人工演示。

5.2 Benchmarking in simulation

  • 可视化模拟拣选任务

  • train data : 8%-由人类操控的演示数据；92%—演示数据重放并加入噪声

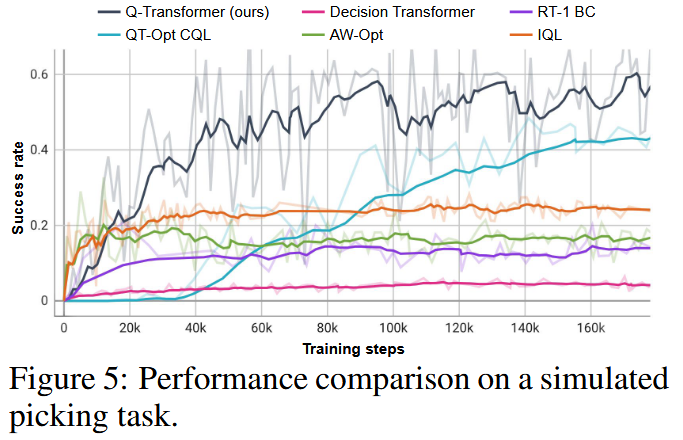
    Q-Transformer 既能够从演示中引导策略，又可以通过 TD 学习传播信息来快速改进。

5.3 消融实验

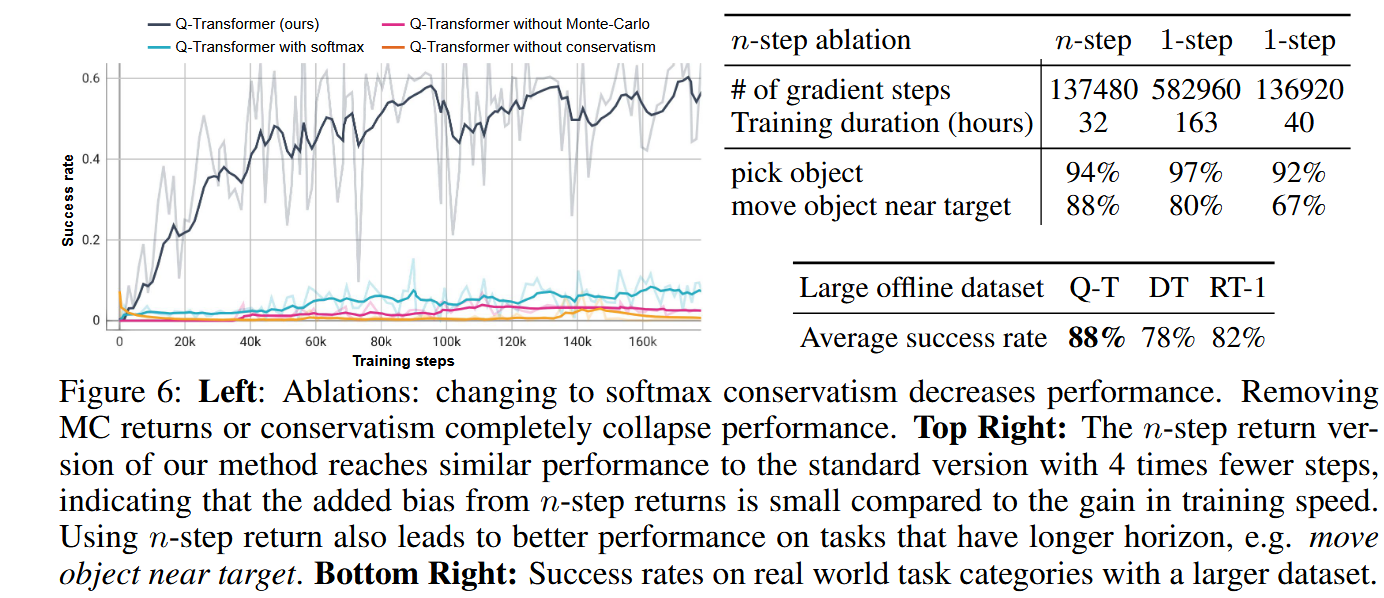
5.4 Massively scaling up Q-Transformer

该实验包括使用 13 个机器人收集的所有数据，包括 RT-1 和成功的自动轨迹的演示，对应于大约 115,000 次成功的试验，以及另外 185,000 次失败的轨迹，总数据集大小约为 300,000 次试验。模型架构和超参数保持完全相同，
结果：Figure 6 (bottom right)

6 Limitations and Discussion

局限：

  • 主要关注稀疏二进制奖励任务
  • 在高维空间下，Q-Transformer采用的动作逐维度离散机制将变得过于复杂。改进方向：基于动作维度分布的自适应离散化
  • 未考虑在线RL
posted @ 2025-02-20 16:00  霜尘FrostDust  阅读(129)  评论(0)    收藏  举报