luogu P1419 题解

题目链接

description

给定一个长度为 \(n\) 的序列（值域为 \([-10^4,10^4]\)）和正整数 \(st,ed\)。

求一个区间，使得其长度 \(\in [st,ed]\) 且平均值最大，输出平均值。

\(1\leq n\leq 10^5\)

solution

这里给出一个复杂度线性的做法。

求出前缀和数组 \(s\)，

答案相当于 \(\max\limits_{1\leq i\leq n}\max\limits_{0\leq j \leq i}\{\dfrac{s_i-s_j}{i-j}\}(st\leq i-j\leq ed)\)

以序列下标为自变量，\(s\) 数组的值为因变量建立平面直角坐标系坐标系。

那么这个分式就表示直线的斜率

分情况讨论（不难讨论但稍有些麻烦，此处略去）可知，所有可能成为最优决策的决策点之间以及和当前点 \((i,s_i)\) 之间，相邻两点所在直线的斜率应单调递增。即当前状态和可能的最优决策点组成下凸壳。

（如图所示）

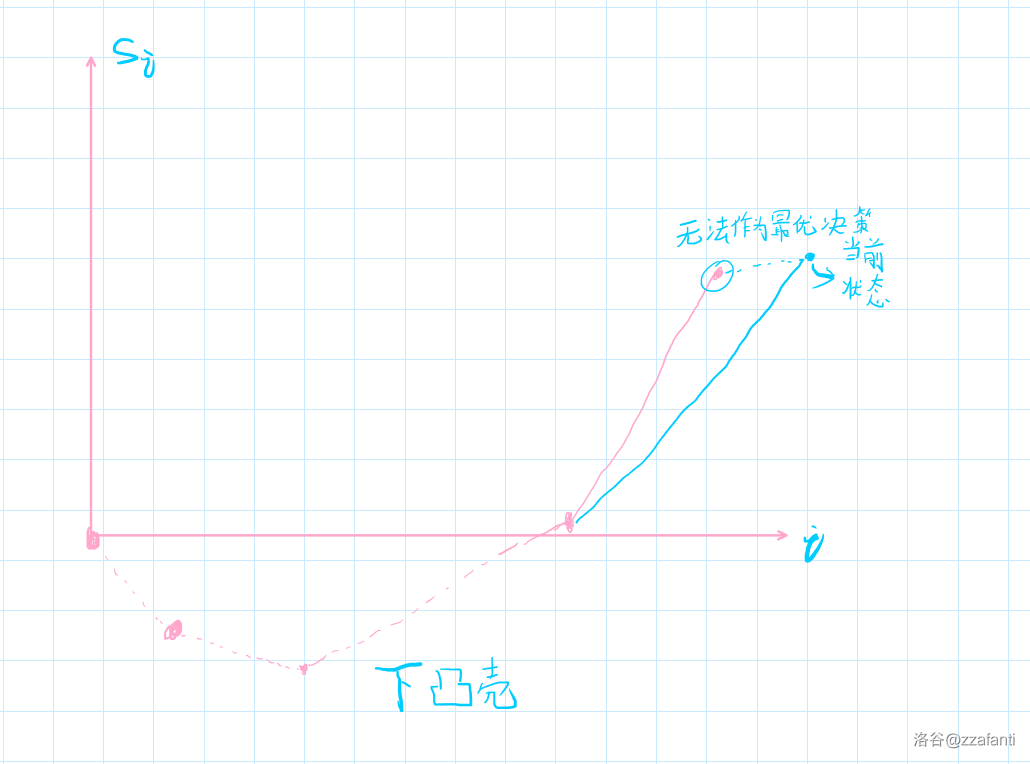
加入一个决策点时，从队尾弹出所有非法的决策点后加入决策点。

求当前的状态的最优决策点时，我们只需从队头扫，找到和当前点斜率最大的决策点即可。（临界状态应该是此时的斜率恰小于当前决策点和下一个决策点的斜率）

我们可以边扫描边将决策点从队首弹出。

这会不会导致后面的某些状态的最优决策点被误弹出呢？

不难发现，状态的纵坐标是单调递增的（前缀和），所以不会出现这种问题（某些题目里不能保证这个性质的话需要在凸壳上二分）。

每个决策点至多出入队一次

时间复杂度 \(O(n)\)

一些闲话

（本文是两个月前写的，忘记发了qwq）

代码不放了吧。

计算斜率要注意 double 的精度。如果用交叉相乘计算的话要注意会不会爆 long long