基础算法篇-买卖股票的最佳时机2

基础算法篇

LeetCode刷题打卡第2天 2022.12.1

买卖股票的最佳时机2

题目描述

给你一个整数数组prices，其中prices[i]表示某只股票第i天的价格。

每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在同一天 出售。

返回你能获得的 最大 利润 。

输入示例

示例1

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

示例2

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

数据范围

• 1 <= prices.length <= 3 * 10 ⁴
• 0 <= prices[i] <= 10⁴

解题思路

思路1

使用贪心算法。这也是比较简单且易想到的方法。

这道题与买卖股票的最佳时机1不一样的是，1限制为只有某一天可以买入一次且在后面的某一天才可以卖出一次，而这题每天都可以买入或者卖出，没有次数限制。所以我们只要在每天股票上升前的时候买入，第二天卖出，如果第三天股票再上升，可以在第二天买入，可以理解为上涨的每天都进行买卖，盈利，股票下降或者平就不交易，不亏钱。

算法流程

引入变量temp，表示每天的股票的差价，即temp = prices[i] - prices[i-1]；变量result表示结果，总盈利。

过程就是遍历整个数组prices[]，记录temp，若为正，则计入总盈利result，否则不给予处理。

Java实现代码

class Solution {
    //贪心算法
    public int maxProfit(int[] prices) {
        int result = 0, temp = 0;
        for (int i = 0; i < prices.length - 1; i++){
            temp = prices[i+1] - prices[i];
            if (temp > 0) {
                result += temp;
            }
        }
        return  result;
    }
}

思路2

来自LeetCode的深搜算法，该算法仅提供思考，由于实际测试数据规模，该算法超时。

将每天交易与否当作树的分叉，可以把整个过程看作一个二叉树，将每条路得到的结果取最大值，就得到我们需要的最终结果。

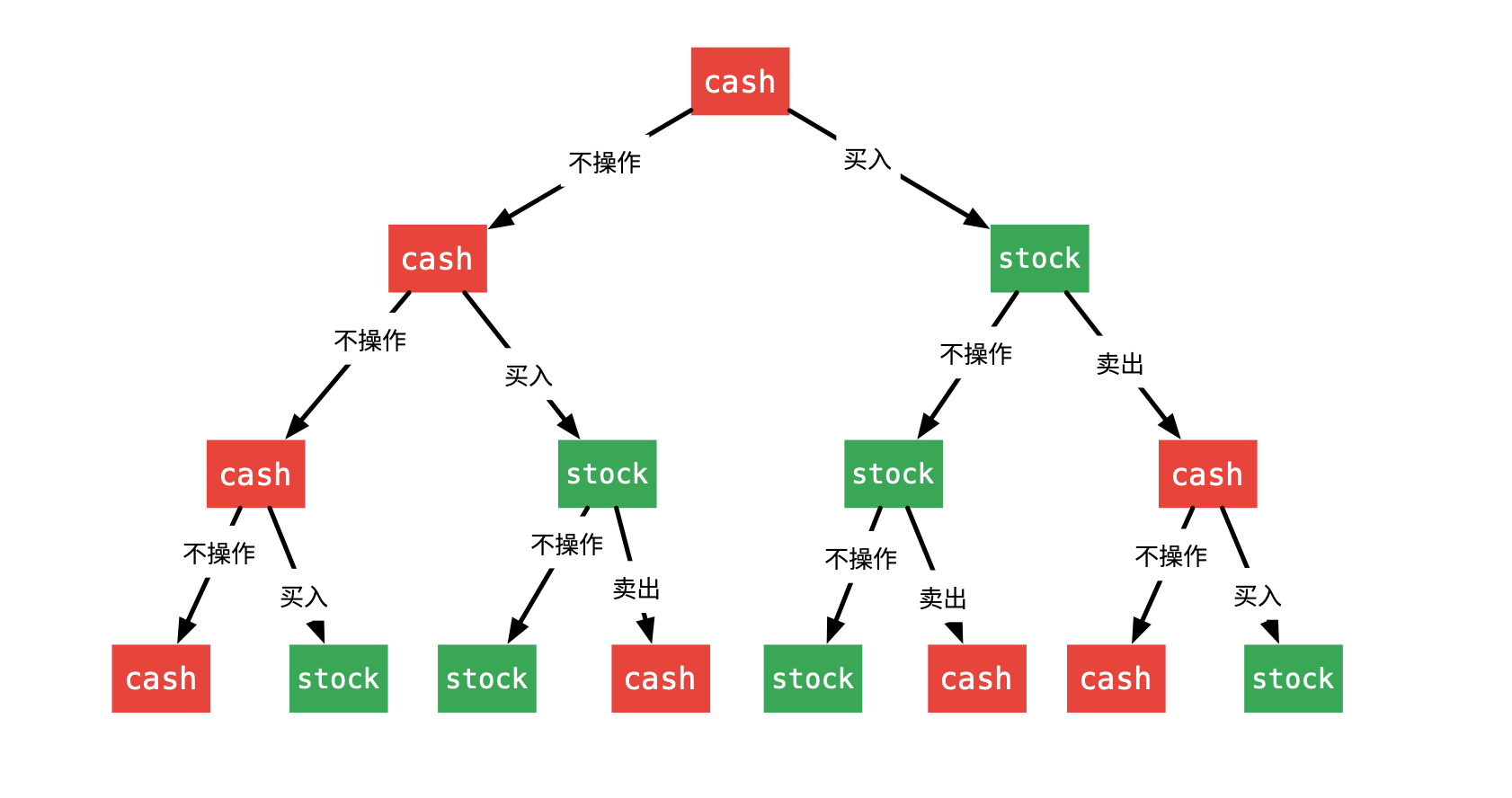
算法流程

从第day = -1天开始（由于数组是从0号为存储），将后一天day + 1选择买入status = 1，则盈利profit = profit - prices[day + 1]，若后一天day + 1选择出售股票 status = 0，则盈利profit = profit + prices[day + 1]。当到达最后一天时day = len - 1，取结果的最大值，并结束当前分支。

Java实现代码

class Solution {
    //深度优先搜索
    private int result = 0;
    public int maxProfit(int[] prices) {
        dfs(prices, -1, prices.length, 0, 0);
        return this.result;
    }
    private void dfs(int[] prices, int day, int len, int status, int profit ) {
        if (day == len - 1) {
            this.result = Math.max(this.result, profit);
            return;
        }
        dfs(prices, day + 1, len, status, profit );
        if (status == 0){
            dfs(prices, day + 1, len, 1, profit - prices[day + 1]);
        } else {
            dfs(prices, day + 1, len, 0, profit + prices[day + 1]);
        }
    }
}

思路3

动态规划思想。

定义 dp[i][0] 表示第 i 天交易完后手里没有股票时获得的最大利润，dp[i][1] 表示第i天交易完后手里还有股票时获得的最大利润。

dp[i][0]的**转移方程 **

第i天交易完之后手里没有股票会有两种情况。第一种情况是 i-1 天交易完之后手里也没有股票，此时第 i 天的最大利润即为前一天手里没有股票的最大利润，即dp[i][0] = dp[i-1][0]；第二种情况是 i - 1天交易完成之后手里有股票，第 i 天交易的时候把该股票给卖了，所以当天之后手里还是没有股票的，此时第 i 天获得的最大利润为前一天手里有股票时的最大利润，加上今天这只股票的价格，即dp[i][0] = dp[i-1][1] + prices[i]。

最终取两者之间的最大利润：dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])。

dp[i][1]的转移方程

这里也会有两种情况。第一种情况是第 i 天没有任何交易，说明手里的股票是 i-1 天就已经购买好的，所以第 i 天的最大利润为 i-1 天手里有股票的最大利润，即dp[i][1] = dp[i-1][1]； 第二种情况是 i-1 天交易完之后手里没有股票，第 i 天的股票是当天新买的，所以第 i 天的最大利润为 i-1 天手里没有股票的最大利润减去第 i 天该股票的价格，即 dp[i][1] = dp[i-1][0] - prices[i]；

最终也取两者之间的最大利润： dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]).

边界条件

• 第一天(i = 0)不购买当天股票：dp[0][0] = 0

• 第一天(i = 0)购买当天股票：dp[0][1] = - prices[0]

Java实现代码

class Solution{
    //动态规划算法
    public int maxProfit(int[] prices) {
        if (prices.length < 2) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][2];
        dp[0][0] = 0;
        dp[0][1] = - prices[0];
        for (int i = 1; i < len; i++ ){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }
        return  dp[len - 1][0];
    }
}

LeetCode参考链接