蒙特卡洛算法

1. 蒙特卡洛方法的基本思想

蒙特卡罗方法又叫统计模拟方法，它使用随机数（或伪随机数）来解决计算的问题，是一类重要的数值计算方法。该方法的名字来源于世界著名的赌城蒙特卡罗，而蒙特卡罗方法正是以概率为基础的方法。

一个简单的例子可以解释蒙特卡罗方法，假设我们需要计算一个不规则图形的面积，那么图形的不规则程度和分析性计算（比如积分）的复杂程度是成正比的。而采用蒙特卡罗方法是怎么计算的呢？首先你把图形放到一个已知面积的方框内，然后假想你有一些豆子，把豆子均匀地朝这个方框内撒，散好后数这个图形之中有多少颗豆子，再根据图形内外豆子的比例来计算面积。当你的豆子越小，撒的越多的时候，结果就越精确。

 

2.例子

蒙特卡洛算法显然可用于近似计算圆周率：让计算机每次随机生成两个0到1之间的数，看这两个实数是否在单位圆内。生成一系列随机点，统计单位圆内的点数与圆外的点数，内接圆面积和正方形面积之比为PI:4，PI为圆周率。，当随机点取得越多时，其结果越接近于圆周率。

 

下面给出c++版本的实现：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
using namespace std;
double in,out,ans;
double x,y,dis;
double getrand()
{
    double ran=0;
    int t=rand()%10000;
    ran=(double)t/10000;
    return ran;
}

int main()
{
    int time=0;
    scanf("%d",&time);
    for(int i=1;i<=time;i++)
    {
        x=getrand()*2;y=getrand()*2;
        dis=sqrt((1-x)*(1-x)+(1-y)*(1-y));
        if(dis>1) out++;
        else in++;
    }
    ans=4*in/(in+out);
    printf("%lf",ans);
    return 0;
} 

 

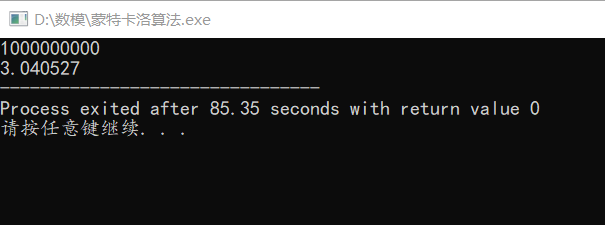
如图，当time的值取1*10^9时，PI的值表示为3.040527，这个值和真实值仍有较大区别，主要原因在cstdlib库中的rand_max，即随机数值的最大范围仅为32767。