线段树学习笔记
开篇
- 区间和:前缀和
- 区间加减值:差分(离线)
- 区间最值:RMQ,单调队列
- 单点修改,区间查询:树状数组
- 单点/区间修改,区间查询:线段树。
Updated at 2025.05.21
Updated at 2025.05.25

线段树
- \(O(nlogn)\) 的复杂度内完成 \(n\) 个数的区间修改
- 单点修改复杂度 \(O(logn)\)
- 线段树采用完全二叉树的方法存储,数组存储,数组长度要开 \(4\times n\)。
建树
//递归建树(a为原始数组,tr为线段树)
int tr[101010], a[10];
void build(int k, int l, int r) { //分别对应:节点标号,对应数组的的区间的左右下标
if (l == r) {
tr[k] = a[l]; //如果是叶子节点
return ;
}
int mid = (l + r) >> 1;
build(k * 2, l, mid);//构造左子树
build(k * 2 + 1, mid + 1, r);//构造右子树
tr[k] = tr[k * 2] + tr[k * 2 + 1];//pushup操作:利用子节点更新父节点
}
单点修改
//单点修改:将原始数组下标为p点的值增加v
void update(int k, int l, int r, int p, int v) {
if (l == p and r == p) {
tr[k] += v;//如果是符合条件的叶节点,直接修改
return ;
}
int mid = l + r >> 1;
if (p <= mid) update(k * 2, l, mid, p, v);
else update(k * 2 + 1, mid + 1, r, p, v);
//pushup: 递归后退,利用子节点更新父节点
tr[k] = tr[k * 2] + tr[k * 2] + 1;
}
区间查询
区间查询:递归到完整的被查询区间包含的节点返回。
1. 判断递归到的节点 \((k,l,r)\) 是否被区间 \((x,y)\) 包含: if(l >= x and r <= y)
2. 如果递归到的节点没有被查询区间包含,判断左右子树是否有贡献
- 左子树答案有贡献:
x <= mid - 右子树对答案有贡献:
y > mid
//区间查询:在下表为k的位置开始,在区间 [x,y] 中查询区间 [l,r] 的区间和
int query(int k,int l,int r,int x,int y){
if(l >= x and r <= y) return tr[k];//全部在 [l,r] 内部,所以全部算上,见图 query-pass
int mid = l+r>>1;
int res = 0;
//分配到左子树,见图 query-left ,因为右子树还有,所以先加到res里
if(x <= mid) res = query(k*2,l,mid,x,y);
//右子树分流,见图 query-right
if(y > mid) res += query(k*2+1,mid+1,r,x,y);
return res;
}
- 图
query-pass
- 图
query-left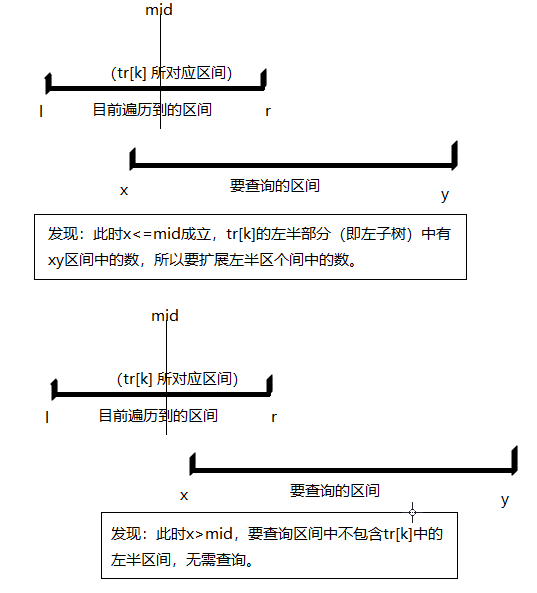
- 图
query-right
数列修改求和2
//板子水过
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
ll tr[N * 4];
int n, m, k, x, y;
void update(int k, int l, int r, int p, int v) {
//单点修改
if (l == p and r == p) {
tr[k] += v;
return ;
}
int mid = l + r >> 1;
if (p <= mid) update(k * 2, l, mid, p, v);
else update(k * 2 + 1, mid + 1, r, p, v);
//pushup
tr[k] = tr[k * 2] + tr[k * 2 + 1];
}
ll query(int k, int l, int r, int x, int y) {
if (l >= x and r <= y) return tr[k];
ll res = 0;
int mid = l + r >> 1;
if (x <= mid) res += query(k * 2, l, mid, x, y);
if (y > mid) res += query(k * 2 + 1, mid + 1, r, x, y);
return res;
}
int main() {
scanf("%d%d",&n,&m);
while(m--){
scanf("%d%d%d",&k,&x,&y);
if(k == 0) update(1,1,n,x,y);
else printf("%lld\n",query(1,1,n,x,y));
}
}
【一本通提高篇线段树】最大数maxnumber
/*
操作1:我们先把所有可能添加到的下标预留出来(数组开好),然后来一个就update一个,一个一个来
操作2:我们直接整区间查询query板子就行。
炸了,l写成1了,MLE调了半天变成RE就是因为这个烦人的字体
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
ll m, p, x;
ll cnt;
char k;
ll tr[N * 4];
void update(int k, int l, int r, int p, int u) {
if (l == p and r == p) {
tr[k] = u;
return ;
}
int mid = l + r >> 1;
if (p <= mid) update(k * 2, l, mid, p, u);
else update(k * 2 + 1, mid + 1, r, p, u);
tr[k] = max(tr[k * 2], tr[k * 2 + 1]); //Warning: 这里是最大数而不是求和
}
ll query(int k, int l, int r, int x, int y) {
if (l >= x and y >= r) {
return tr[k];
}
ll res = 0;
int mid = l + r >> 1;
if (x <= mid) {
res = max(res, query(k * 2, l, mid, x, y));
}
if (y > mid) res = max(res, query(k * 2 + 1, mid + 1, r, x, y));
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> m >> p;
int ans = 0;//记录上一次query的值
for (int i = 1; i <= m; i++) {
cin >> k >> x;
if (k == 'A') update(1, 1, m, ++cnt, (x + ans) % p);
else {
ans = query(1, 1, m, cnt - x + 1, cnt);
cout << ans << "\n";
}
}
return 0;
}
树状数组练习B.-【一本通提高篇树状数组】 数星星
/*
其实这个题在我的树桩数组专题里面也有,更详细。
题意就是让我们统计对于这所有的点中的每一个点,x和y同时小于或等于它的点的数量。
不难发现(如果你认真读题的话),输入现在已经把y帮你排好序了,那我们只要输入一个统计一个就无需计算y的点了,因为在这个点之前的所有输入过的点的y都是满足条件的。
只需要统计x即可。我们每次输入一个就update一下,我们把线段树上的x给update加1,然后再跑一遍query就能得出这个值了,query的是小于它的数的值。
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 4e4+10;
int tr[N * 4], n, x, y;
int ans[N];
#define ls k*2
#define rs k*2+1
void update(int k, int l, int r, int p, int v) {
if (l == p and r == p) {
tr[k] += v;
return ;
}
int mid = l + r >> 1;
if (p <= mid) update(ls, l, mid, p, v);
if (p > mid) update(rs, mid + 1, r, p, v);
tr[k] = tr[ls] + tr[rs]; //pushup;
}
int query(int k,int l,int r,int x,int y){
if(l >= x and r <= y){
return tr[k];
}
int mid = l+r>>1,res = 0;
if(x <= mid) res += query(ls,l,mid,x,y);
if(y > mid) res += query(rs,mid+1,r,x,y);
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &x, &y);
x++,y++;
cout<<query(1, 1, 40000, 1, x)<<"\n";
update(1, 1, 40000, x, 1);
}
}
不稳定的数字
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int tr[N * 4];
int l[N], r[N], n, b[N], a[N];
#define ls k*2
#define rs k*2+1
void update(int k, int l, int r, int p, int v) {
if (l == p and r == p) {
tr[k] += v;
return ;
}
int mid = l + r >> 1;
if (p <= mid) update(ls, l, mid, p, v);
else update(rs, mid + 1, r, p, v);
tr[k] = tr[ls] + tr[rs];
}
int query(int k, int l, int r, int x, int y) {
if (l >= x and r <= y) {
return tr[k];
}
int mid = l + r >> 1, res = 0;
if (x <= mid) res += query(ls, l, mid, x, y);
if (y > mid) res += query(rs, mid + 1, r, x, y);
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &b[i]);
a[i] = b[i];
}
sort(b + 1, b + 1 + n);
int k;
k = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + 1 + k, a[i]) - b;
l[i] = query(1, 1, k, a[i] + 1, k);
update(1, 1, k, a[i], 1);
}
memset(tr, 0, sizeof tr);
for (int i = n; i >= 1; i--) {
r[i] = query(1, 1, k, a[i] + 1, k);
update(1, 1, k, a[i], 1);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
int ma = max(l[i], r[i]);
int mi = min(l[i], r[i]);
if (ma > mi * 2) ans++;
}
printf("%d", ans);
}
区间修改
- 递归到完整的被修改区间 \([x,y]\) 所包含的结点。
- 修改本节点的值,打懒标记(
lazytag)
懒标记:当前节点所有子孙节点未来要加上的数。
标记下放:什么时候向下递归顺便下放懒标记。
Luogu: 线段树1
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
typedef long long ll;
ll tr[N * 4], lazytag[N * 4];
int a[N], n, m;
#define ls k*2
#define rs k*2+1
void build(int k, int l, int r) {
if (l == r) tr[k] = a[l];
else {
int mid = l + r >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
tr[k] = tr[ls] + tr[rs];
}
}
void change(int k, int l, int r, int v) {
tr[k] += (ll)v * (r - l + 1);
lazytag[k] += v;
}
void pushdown(int k, int l, int r) {
if (lazytag[k] != 0) {
int mid = l + r >> 1;
change(ls, l, mid, lazytag[k]);
change(rs, mid + 1, r, lazytag[k]);
lazytag[k] = 0;
}
}
void modify(int k, int l, int r, int x, int y, int v) {
if (l >= x and r <= y) {
change(k, l, r, v);
return ;
}
pushdown(k, l, r);
int mid = l + r >> 1;
if (x <= mid) modify(ls, l, mid, x, y, v);
if(y > mid) modify(rs, mid + 1, r, x, y, v);
tr[k] = tr[ls] + tr[rs];
}
ll query(int k, int l, int r, int x, int y) {
if (l >= x and r <= y) {
return tr[k];
}
pushdown(k, l, r);
int mid = l + r >> 1;
ll res = 0;
if (x <= mid) res += query(ls, l, mid, x, y);
if (y > mid) res += query(rs, mid + 1, r, x, y);
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
build(1, 1, n);
char c;
for (int i = 1; i <= m; i++) {
cin >> c;
if (c == 'C') {
int d, x, y;
cin >> x >> y >> d;
modify(1, 1, n, x, y, d);
} else {
int x, y;
cin >> x >> y;
cout << query(1, 1, n, x, y) << '\n';
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号