Loading

2025dsfz集训Day11：数位DP、状态压缩DP、单调队列优化DP

Day11：数位DP、状压DP、单调队列优化DP

经典题目：AccodersP2195 |【一本通提高数位动态规划】Amount of Degrees

题意： 求出区间 \([x,y]\) 中满足下面条件的所有的数：这个数 \(x\) 可以用 \(k\) 个不相等的 \(b\) 的整数幂之和。

首先这个区间是满足区间减法的。因此我们可以只考虑，\([0,y]\) 和 \([0,x-1]\) 这两个区间内的个数。

再考虑这些数的性质， 这些数转化成 \(b\) 进制以后，每一数位上的值都是 \(0\) 或 \(1\)；

那么就可以在数位上下手。然后我们就可以建一棵完全二叉树，完全二叉树的节点上依次填写 \(0\) 和 \(1\)，这样子，从根到叶子节点的路径就可以表示一个值。对于我们想要的数字，就是这条路径上的 \(1\) 的个数必须是 \(k\)个。对于各个子问题，我们可以预先处理处，到第 \(i\) 层有 \(j\) 个 \(1\)。这个就是一个简单的 \(dp\)。

然后对于 \(b\) 进制，我们可以把 \(n\) 转化成 \(b\) 进制之后，去找一个不超过 \(n\) 最大的满足条件的数，在把 \(b\) 进制直接当成 \(2\) 进制来做就可以。怎么去找这个‘最大’的数呢？就只在把 \(n\) 转化为 \(b\) 进制之后，从左边开始找到

第一个数位上不为 \(0\) 或 \(1\) 的位置，再把这个位置，和这个位置右边的所有数位上的值改为 \(1\) 。就可以了。

点击查看代码 
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

const int N = 35;

int X, Y, K, B;
int C[N][N]; //C[n, m] n个里选m个 

void init(int n) {
	C[1][1] = C[1][0] = 1;
	for (int i = 2; i <= n; i ++ ) {
		C[i][0] = 1;
		for (int j = 1; j <= i; j ++ ) C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; 
	}
}

int dp(int n) {
	if (!n) return 0; // 非法边界 
	
	vector<int> nums;
	while(n) nums.push_back(n % B), n /= B; // 将数按位分解 
	
	int res = 0; // 问题答案 
	int last = 0; // 向下走时父亲的信息(此题是使用了多少个1)
	for (int i = nums.size() - 1; i >= 0 ; i -- ) { // 最高位向最低位枚举 
		int x = nums[i];
		if (x == 1) {
			res += C[i][K - last];
			last ++;
			if(last > K) break;
		}
		else if (x > 0) {
			res += C[i][K - last];
			if (K - last - 1 >= 0)  res += C[i][K - last - 1];
			break;
		}
		
		if(!i && last == K) res ++ ;
		
	}
	
	return res;
} 

int main() {
	
	scanf("%d%d%d%d", &X, &Y, &K, &B);
	init(N - 1);
	printf("%d\n", dp(Y) - dp(X - 1));
	return 0;
}

洛谷P2657 [SCOI2009] windy 数

设f(x)表示x前面的数 即 \(t∈[1,x)\) 中 \(windy\) 数的个数
那么显然如果要求 \([l,r]\) 中 \(windy\) 数的个数就是：

\(F(l,r) = f（r+1）-f(l)\)
数位 \(dp\) 开始，预处理位数为 \(i\) 最高位为 \(j\) 的 \(windy\) 数个数 \(f[i][j]\)

转移：

\(f[i][j]=f[i-1][k]\) | 其中k是非负整数 \(k∈[0,9]\) 且 \(|k-j|>=2\)
初始值：

\(f[1][i]=1\) | 其中 \(i\) 为非负整数 \(i∈[0,9]\)
求 \(f(x)\) 怎么求呢？

为了方便处理先对数 \(x\) 进行按 \(10\) 进制位拆分到 \(a[]\) 数组

显然位数比 \(x\) 要小的数字都是合法的都在 \([1,x）\) 区间内，直接统计就行
位数和 \(x\) 一样最高位的数字比 \(x\) 小的数字都是合法的都在 \([1,x）\) 区间内直接统计就行
位数和 \(x\) 一样，最高位又和 \(x\) 一样我们从左到右扫一遍 \(x\) 各个位子上的数字大小然后枚举合法的该位子上的数 \([0,9]\) 判断是否合法就行。

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[15][15],ans;
int a[15],len;
long long L,R;
ll dfs(int pos,int pre,int st,int limit){
	if(pos>len) return 1;
	if(!limit&&dp[pos][pre]!=-1) return dp[pos][pre];
	ll ret=0;
	int res=limit?a[len-pos+1]:9;
	for(int i=0; i<=res; i++){
		if(abs(i-pre)<2) continue;
		if(st&&i==0) ret+=dfs(pos+1,-2,1,limit&&i==res);
		else ret+=dfs(pos+1,i,0,limit&&i==res);
	}
	if(!limit&&!st) dp[pos][pre]=ret;
	return ret;
}
void part(ll x){
	len=0;
	while(x) a[++len]=x%10,x/=10;
	memset(dp,-1,sizeof dp);
	ans=dfs(1,-2,1,1);
}
int main(){
	scanf("%lld%lld",&L,&R);
	part(L-1);
	ll minn=ans;
	part(R);
	ll maxx=ans;
	printf("%lld",maxx-minn);
	return 0;
}

单调队列优化DP

单调队列

  • 队列是单调的，递增或递减
  • 只能在队首或者队尾进行操作
  • 队列中维护所有在窗口中的元素，有一些元素是没用的，以区间最大值为例:
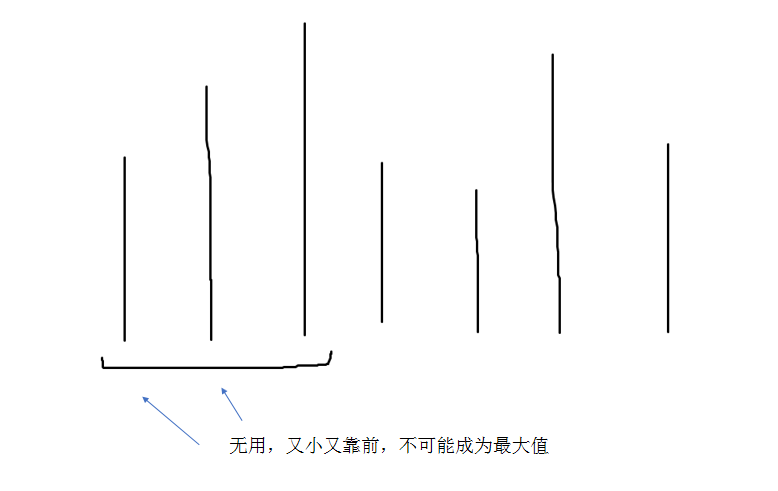
    • 所以从左到右尝试加入队列，弹出队尾比当前数更小的元素，弹出队首已经出窗口的元素，再队尾压入当前数
    • 这样，队首就是窗口最大值
  • 每个数只会弹入弹出一次，复杂度O(n)
点击查看单调队列模版 
void getmax() {  // 和上图同理
    int head = 0, tail = -1;
    for (int i = 1; i <= k; i++) {
        while (head <= tail) {
            tail--;  // 移动窗口（见下文）+优化队列
        }
        q[++tail] = i;  // 入队
    }
    for (int i = k; i <= n; i++) {
        while (head <= tail && a[q[tail]] <= a[i]) tail--;  // 排除没用的值，优化队列内容。（详见上图）
        cout << a[q[head]] << "";                           // 输出最大值
    }
}
经典例题：

题意

  • 给出一个长度为 \(n\) 的数组，编程输出每 \(k\) 个连续的数中的最大值和最小值。
  • \(n,k≤1e6\)
点击查看代码 
#include <bits/stdc++.h>
using namespace std;

int a[1001010];
deque <int> id;
deque <int> q;
int k, n;
int main() {
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i];

	for (int i = 1; i <= k; i++) {
		while (!q.empty() and q.back() > a[i]) {
			q.pop_back();
			id.pop_back();
		}
		q.push_back (a[i]);
		id.push_back (i);
	}
	for (int i = k + 1; i <= n + 1; i++) {
		cout << q.front() << " ";
//		cout << q.back() << endl;
		if (id.front() < i - k + 1) {
			id.pop_front();
			q.pop_front();
		}
		while (!q.empty() and q.back() > a[i]) {
			q.pop_back();
			id.pop_back();
		}

		q.push_back (a[i]);
		id.push_back (i);

	}
	for (int i = 1; i <= k; i++) {
		while (!q.empty() and q.back() < a[i]) {
			q.pop_back();
			id.pop_back();
		}
		q.push_back (a[i]);
		id.push_back (i);
	}
	cout<<endl;
	for (int i = k + 1; i <= n + 1; i++) {
		cout << q.front() << " ";
//		cout << q.back() << endl;
		if (id.front() < i - k + 1) {
			id.pop_front();
			q.pop_front();
		}
		while (!q.empty() and q.back() < a[i]) {
			q.pop_back();
			id.pop_back();
		}

		q.push_back (a[i]);
		id.push_back (i);

	}
}

最大连续和

  • 给你一个长度为n的整数序列。要求从中找一段连续长度不超过m的子序列，并且和最大
  • 求前缀和，转化成:

\[a[i]=max(sum(i)-sum(i-k)|k=1\dots m) \]

  • 即:

\[a[i]=sum(i)-min(sum(i-k)|k=1\dots m) \]

  • 滑动窗口求第二项即可
点击查看代码 
int MaxSubSequence(const int A[], int N){  
    int ThisSum,MaxSum,i,j,k;  
    MaxSum = 0;  
    for(i=0;i<N;i++)  
    {  
        for(j=i;j<N;j++)  
        {  
            ThisSum = 0;  
            for(k=i;k<=j;k++)  
            {  
                ThisSum += A[k];  
            }  
            if(ThisSum > MaxSum)  
                MaxSum = ThisSum;  
        }  
    }  
    return MaxSum;  
}

修建草坪

  • \(FJ\) 有 \(N\) (\(1 <= N <= 100,000\))只排成一排的奶牛。每只奶牛的效率是不同的，奶牛 \(i\) 的效率为 \(E_i\)。
    计算 \(FJ\) 选奶牛可以得到的最大效率，并且该方案中没有连续的超过 \(K\) 只奶牛。

  • 设 \(dp[i][0]\) 表示以i为结尾不选i的最大值， \(dp[i][1]\) 表示以 \(i\) 为结尾选 \(i\) 的最大值:

\[dp[i][0]=max(dp[i-1][0],dp[i-1][1]) \]

\[dp[i][1]=max(dp[j][0]+sum[i]-sum[j]|i-k\le j\le i-1) \]

转化成

\[dp[i][1]=sum[i]+max(dp[j][0]-sum[j]|i-k\le j\le i-1) \]

可以单调队列优化.

点击查看代码 
#include <bits/stdc++.h>
typedef long long LL;
const int maxn = 100010;
LL dp[maxn], sum[maxn];
int que[maxn], E[maxn];
int head, tail;
LL max(LL a, LL b) {
    return a > b? a : b;
}
void add(int j) {
    while (head < tail && dp[j - 1] - sum[j] >= (que[tail - 1] > 0 ? dp[que[tail - 1] - 1] : 0) - sum[que[tail - 1]]) {
        --tail;
    }
    que[tail++] = j;
}
void del(int j) {
    if (head < tail && que[head] == j) {
        ++head;
    }
}
int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    sum[0] = 0;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &E[i]);
        sum[i] = sum[i - 1] + E[i];
    }
    dp[0] = 0;
    que[tail++] = 0;
    for (int i = 1; i <= n; ++i) {
        add(i);
        del(i - k - 1);
        int j = que[head];
        dp[i] = (j > 0 ? dp[j - 1] : 0) + sum[i] - sum[j];
    }
    LL ans = max(dp[n], dp[n - 1]);
    printf("%lld\n", ans);
    return 0;
}

旅行问题

  • \(John\) 打算驾驶一辆汽车周游一个环形公路。公路上总共有 \(n\) 个车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。 \(John\) 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。在一开始的时候，汽车内油量为零，\(John\) 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。
  • 判断以每个车站为起点能否按条件成功周游一周。

解法

  • 拆环成链，设每个加油站有 \(d[i]\) 油，到下一个加油站要 \(s[i]\) 千米
  • 那么从一个点出发，\(d[i]-s[i]\) 前缀和必须是非负数
  • 在 \(2n\) 的链上维护 \(n\) 的滑动窗口，求区间最小值，判断是不是负数
点击查看代码 
#include <bits/stdc++.h>
#define int long long

std::deque<int> q;
int n;
int b[2000001], a[2000001], ans[2000001];

signed main() {
	scanf("%lld", &n);
	for (int i = 1, x, y; i <= n; i++) {
		scanf("%lld %lld", &x, &y);
		a[i + n] = a[i] = x - y;
		int d = n - i == 0 ? n : n - i;
		b[d + n] = b[d] -= y;
		b[2 * n - i + 1] = b[n - i + 1] += x;
	}
	for (int i = 2; i <= n * 2; i++)
		a[i] += a[i - 1], b[i] += b[i - 1];
	for (int i = 1; i < n * 2; i++) {
		while (q.size() && i - q.front() + 1 > n)
			q.pop_front();
		while (q.size() && a[i] <= a[q.back()])
			q.pop_back();
		q.push_back(i);
		if (i >= n) {
			if (a[q.front()] - a[i - n] >= 0)
				ans[i - n + 1] = 1;
		}
	}
	q.clear();
	for (int i = 1; i < n * 2; i++) {
		while (q.size() && i - q.front() + 1 > n)
			q.pop_front();
		while (q.size() && b[i] <= b[q.back()])
			q.pop_back();
		q.push_back(i);
		if (i >= n) {
			if (b[q.front()] - b[i - n] >= 0)
				ans[2 * n - i] = 1;
		}
	}
	for (int i = 1; i <= n; i++)
		if (ans[i])
			printf("TAK\n");
		else
			printf("NIE\n");
}

BANK NOTEs

  • 一共有 \(n\) 种面值的硬币,面值分别为 \(b_1, b_2,..., b_n\). 但是每种硬币有 \(c_i\) 个,现在我们想要凑出面值 \(k\) 求最少要用多少个硬币.

  • \[n≤200,b_i,c_i,k≤20000 \]

单调队列优化多重背包

不了解背包 \(DP\) 的请先阅读背包 \(DP\)。设 \(f_{i,j}\) 表示前 \(i\) 个物品装入承重为 \(j\) 的背包的最大价值，朴素的转移方程为

\[f_{i,j}=\max_{k=0}^{k_i}(f_{i-1,j-k\times w_i}+v_i\times k) \]

时间复杂度 \(O(W\sum k_i)\)
考虑优化\(f_i\)的转移。为方便表述，设\(g_{x,y}=f_{i,x\times w_i+y}, g'_{x,y}=f_{i-1,x\times w_i+y}\)，其中\(0\leq y<w_i\)，则转移方程可以表示为:

\[g_{x,y}=\max_{k=0}^{k_i}(g'_{x-k,y}+v_i\times k) \]

设\(G_{x,y}=g'_{x,y}-v_i\times x\)。则方程可以表示为:

\[g_{x,y}=\max_{k=0}^{k_i}(G_{x-k,y})+v_i\times x \]

这样就转化为一个经典的单调队列优化形式了。\(G_{x,y}\) 可以 \(O(1)\) 计算，因此对于固定的 \(y\)，我们可以在 \(O\left(\left[\frac{W}{w_i}\right]\right)\) 的时间内计算出 \(g_{x,y}\)。因此求出所有 \(g_{x,y}\) 的复杂度为

\[O\left(\left[\frac{W}{w_i}\right]\right)\times O(w_i)=O(W)。 \]

这样转移的总复杂度就降为 \(O(nW)\)。

点击查看代码 
#include <bits/stdc++.h>
using namespace std;
const int N=205,M=20005;
int n,m,B[N],C[N],dp[M];
struct Data {
	int Shuz,Weiz;
} Ddq[M];
int main() {
	int i,j,k;
	cin>>n;
	for(i=1; i<=n; i++) cin>>B[i];
	for(i=1; i<=n; i++) cin>>C[i];
	cin>>m;
	memset(dp,63,sizeof dp);
	dp[0]=0;
	for(i=1; i<=n; i++) {
		for(j=0; j<B[i]; j++) {
			int Head=1,Tail=0;
			for(k=0;; k++) {
				int x=k*B[i]+j;
				if(x>m) break;
				while(Head<Tail&&Ddq[Head].Weiz<k-C[i]) Head++;
				while(Head<=Tail&&dp[x]-k<Ddq[Head].Shuz-Ddq[Head].Weiz) Tail--;
				Ddq[++Tail]= {dp[x]-k,k};
				dp[x]=min(dp[x],Ddq[Head].Shuz+k);
			}
		}
	}
	cout<<dp[m]<<endl;
	return 0;
}

烽火传递

  • 在某两座城市之间有 \(n\) 个烽火台，每个烽火台发出信号都有一定的代价。为了使情报准确的传递，在连续 \(m\) 个烽火台中至少要有一个发出信号。现输入 \(n\) 、\(m\) 和每个烽火台发出的信号的代价，请计算总共最少需要话费多少代价，才能使敌军来袭之时，情报能在这两座城市之间准确的传递.

  • \[1<=m<=n<=1,000,000 \]

  • 状态表示：\(f[i]\) 标识前 \(i\) 个烽火台并点燃第 \(i\) 个烽火台的最小合法代价.
  • 状态转移：\(f[i]=min(f[j]+w[i],i-m\le j\le i-1)\),最后扫描 \(m\) 个 \(f[i]\) 的值。
点击查看代码 
#include <bits/stdc++.h>
using namespace std;
int dp[100010];
int a[100010];
int q[100010];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    int head=1;//表示队首的下标。
    int tail=1;//表示队尾的下标。
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
    for(int i=1;i<=n;i++){
        dp[i]=dp[q[head]]+a[i];
        while(tail>=head&&dp[i]<=dp[q[tail]])//每次更新都表示弹出队尾元素。
            tail--;
        q[++tail]=i;//弹完后，我们保证这个队列是单调的且新加入的元素一定是队尾元素。
        while(q[head]<i+1-m)//判断队首元素是否合法，如果不合法，将其弹掉。
            head++;
    }
    printf("%d",dp[q[head]]);//这一步比较经典。我们维护的单调队列中，队首元素一定是合法的(在最后的m个烽火台之内)，
    //所以我们选择这其中的最小者更新即可
    return 0;
}
posted @ 2025-01-23 20:18  FrankWkd  阅读(54)  评论(0)    收藏  举报