2025dsfz集训Day8：线段树

Day8：线段树

前言：线段树听起来很高大尚，就是儿子节点表示法的树。几乎一样。

\[Designed\ By\ FrankWkd\ -\ Luogu@Lwj54joy,uid=845400 \]

特别感谢此次课的主讲：安玺儒 (天津大学)

关于线段树

线段树是算法竞赛中常用的用来维护区间信息的数据结构。线段树可以在 \(O(log N)\) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。
线段树的本质：本质上是一颗二叉树，树上每个点都对应了一个区间，区间一分为二为该点对应的左右子节点。每个点可以维护对应区间的信息。

线段树建树

给出 \(a[] = \{1, 9, 2, 6, 0, 8, 1, 7\}\)，可以构建出如下线段树：

点击查看代码

struct node {
	int ls, rs, sum, lazytag;
} a[10000];//数组开4倍大小

void bulid(int k, int l, int r) {
	if (l == r) {
		a[k].sum = t[l];//已经到了叶节点,t[l]是输入的数
		return;
	}
	bulid(k * 2, l, l + r >> 1);//递归左孩子
	bulid(k * 2 + 1, (l + r >> 1) +1, r);//递归右孩子
	t[k].sum = t[k * 2].sum + t[k * 2 + 1].sum;
	//将左右孩子的sum相加可得其作为根节点的数值总和
}

线段树的操作

区间查询

利用线段树的树状结构，我们可以从根节点向下缩小区间，找到想要查询的区间。
由于查询的区间会被包含在当前线段树区间，因此总共分为三种情况：
- 查询区间完全被包含在左子树的区间内，
- 查询区间完全被包含在右子树的区间内，
- 查询区间横跨左子树的区间和右子树的区间。
不同情况的解法：
- 1：直接递归到左子树中，抛弃右子树。
- 2：同情况一，抛弃左子树。
- 3：将查询的区间分为 \(l,mid\) 和 \(mid,r\)，然后到左右子树中分别查询。

点击查看代码

int query(int k, int l, int r, int p, int q) {
	//l,r为当前线段树的区间，p,q为想要查询的区间
	if (p == l && r == q) return t[k].sum; //找到直接返回
	int mid = l + r >> 1;
	if (q <= mid) return query(ls, l, mid, p, q); //情况1
	else if (p > mid) return query(rs, mid + 1, r, p, q); //情况2
	else return query(ls, l, mid, p, mid) + query(rs, mid + 1, r, mid + 1, q); //情况3
}

单点修改

与建树的思路相同，利用递归的思想。
- 先向下递归子树的信息，子树的信息计算好后将信息传回父节点。
- 递归同查询思路，分三种情况。递归终止条件是遇到叶子节点。

点击查看代码

int modify(int k, int l, int r, int pos, int val) {
	if (l == r) {//找到了叶节点(答案)
		t[k].sum += val;//
		return ;
	}
	int mid = l + r >> 1;
	if (pos <= mid)modify(ls, l, mid, pos, val);//如果在右子树中，向右子树递归
	else modify(rs, mid + 1, r, pos, val);//否则向左子树递归
	t[k].sum = t[ls].sum + t[rs].sum;//修改要修改的节点的祖先节点的值
}

将线段树的区间内每个数加上 x：懒标记

如果我们像单点修改的思路去做, 那么我们每次修改的复杂度高达 \(O(n log n)。\) 我们发现一个大区间, 我们只需最多 \(log n\) 个节点代表的区间就可以表达, 我们可以利用这个性质, 给这些区间的节点打上标记。
懒标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
说人话，就是标记祖先节点，在别的操作中遍历到当前的点时，将当前要传给叶子结点的修改数转移到子节点上。
以最开始的数组 \(a[] = \{1, 9, 2, 6, 0, 8, 1, 7\}\) 举例: 我们要对区间 [3, 8] 每个数加上 2:
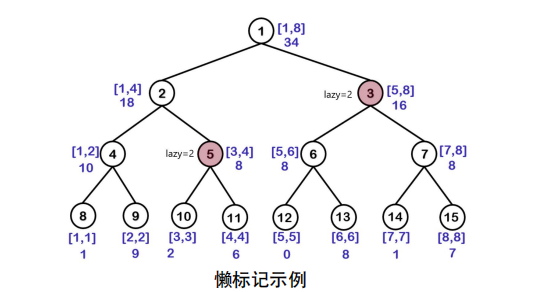
直接标记懒标记在祖先节点

点击查看代码

void modify(int k, int l, int r, int p, int q, ll val) {
	if (p == l && r == q) {
		put_tag(k, l, r, val);    //新增加的语句
		return ;
	}
	pushdown(k, l, r); //新增加的语句
	int mid = l + r >> 1;
	if (q <= mid)modify(ls, l, mid, p, q, val);
	else if (p > mid)modify(rs, mid + 1, r, p, q, val);
	else modify(ls, l, mid, p, mid, val),
		     modify(rs, mid + 1, r, mid + 1, q, val);
	pushup(k);
}
ll query(int k, int l, int r, int p, int q) {
	if (p == l && r == q)return t[k].sum;
	pushdown(k, l, r); //新增加的语句
	int mid = l + r >> 1;
	if (q <= mid)return query(ls, l, mid, p, q);
	else if (p > mid)return query(rs, mid + 1, r, p, q);
	else return query(ls, l, mid, p, mid)
		            + query(rs, mid + 1, r, mid + 1, q);
}
void pushup(int k) {
	t[k].sum = t[ls].sum + t[rs].sum;
}
void pushdown(int k, int l, int r) {
	if (t[k].lz) {
		int mid = l + r >> 1;
		t[ls].sum += (mid - l + 1) * t[k].lz;
		t[rs].sum += (r - mid) * t[k].lz;
		t[ls].lz += t[k].lz;
		t[rs].lz += t[k].lz;
		t[k].lz = 0;
	}
}
void put_tag(int k, int l, int r, int val) {
	t[k].sum += 1ll * (r - l + 1) * val;
	t[k].lz += val;
}

其中，

\(pushup\) 函数的作用是将其祖先赋值为其子节点的和，相当于 \(bulid\) 函数的最后一句。
\(put\_tag\) 函数的作用是标记祖先节点的懒标记，将其懒标记的值设为要加上的值
\(pushdown\) 函数的作用是将当前要传给叶子结点的修改数转移到子节点上。
- \(pushdown\) 函数的核心代码是：
  点击查看代码
```
int mid = l + r >> 1;
t[ls].sum += (mid - l + 1) * t[k].lz;
t[rs].sum += (r - mid) * t[k].lz;
t[ls].lz += t[k].lz;
t[rs].lz += t[k].lz;
t[k].lz = 0;
```
  这段代码非常烂，可以写成很好理解的下面一段代码：
  点击查看代码
```
put_tag(ls);
put_tag(rs);
t[k].lz = 0;
```

个人码风建议

注：因为蒟蒻经常去你谷~~抄题解~~，所以经常要阅读很多程序，所以在这方面很注重，如果你不喜欢规规矩矩或者是你只是想速通线段树，请略过。

变量与函数

其他风格有把线段树节点的左右端点存进结构体中，函数变量中没有线段树节点对应区间的左右端点。
个人推荐将左右端点放进函数变量中, 虽然略显繁琐但节省空间。

点击查看实例代码

int query(int k, int l, int r, int p, int q) {
	//k代 表 当 前 线 段 树 节 点 编号 ,p,q代 表 查 询 区 间 左 右 端 点
	//l,r代 表 当 前 线 段 树 节 点 对 应 区 间 左 右 端 点
	...
}

递归与判断

以查询举例, 有的码风会将三种情况合并为两种情况进行判断。
个人推荐将三种情况分别列出, 便于使用懒标记永久化。

点击查看代码

int query(int k, int l, int r, int p, int q) {
	...
	if (q <= mid) return query(ls, l, mid, p, q);
	else if (p > mid) return query(rs, mid + 1, r, p, q);
	else return query(ls, l, mid, p, mid) + query(rs, mid + 1, r, mid + 1, q);
}

懒标记永久化

为什么使用懒标记永久化？
- 部分特殊的线段树下传懒标记的代价过大，或不支持下传懒标记。例如可持久化 / 动态开点线段树，下传懒标记需要新建结点，空间常数过大；又例如树套树，无法下传懒标记。
与临时懒标记的区别？
- 未永久化的懒标记：表示暂时未对左右子树的操作，在后续求值或进
  一步修改时会下放。永久化的懒标记：表示已经进行对左右子树的操作，在后续求值时不会下放，需要在求值的路径上记录下来，并计入答案中。
使用条件：
- 需要满足区间修改的必要条件，如信息打上标记后可以快速计算。
- 修改必须与顺序无关，即标记具有交换律。（一个特例是区间赋值，区间赋值虽然与修改顺序相关，但可以通过维护时间戳转化为求时间戳最值）
- 懒标记在线段树路径上累加不会溢出。

点击查看代码

void modify(int k, int l, int r, int p, int q, ll val) {
	t[k].sum += val * (q - p + 1);
	if (p == l && q == r) {
		t[k].lz += val;
		return ;
	}
	int mid = l + r >> 1;
	if (q <= mid) modify(ls, l, mid, p, q, val);
	else if (p > mid) modify(rs, mid + 1, r, p, q, val);
	else modify(ls, l, mid, p, mid, val), modify(rs, mid + 1, r, mid + 1, q, val);
}
ll query(int k, int l, int r, int p, int q, ll lz) {
	if (p == l && q == r) return t[k].sum + lz * (r - l + 1);
	int mid = l + r >> 1;
	if (q <= mid) return query(ls, l, mid, p, q, lz + t[k].lz);
	else if (p > mid) return query(rs, mid + 1, r, p, q, lz + t[k].lz);
	else return query(ls, l, mid, p, mid, lz + t[k].lz) + query(rs, mid + 1, r, mid + 1, q, lz + t[k].lz);
}

线段树的空间复杂度优化

前面说过线段树需要提前开出来 \(4 × n\) 的大小的数组，有些节点可能从开始到结束一直没有被用过，造成了空间的浪费。如何优化？

动态开点

动态开点的核心思想：结点只有在有需要的时候才会创建。为了节省空间，每次我们可以开始不建好树，最初只建立一个根节点，每次我们需要访问一个子区间时，才建立代表这个区间的子结点。这样可能会导致结点的编号没有父子结点编号二倍的关系，因此我们需要将每个结点的子节点位置记录下来。
单次操作的复杂度是 \(O(log n)\)，\(m\) 次单点操作后结点的规模是
\(O(m log n)\)。最多也只需要 \(2n − 1\) 个结点，并且没有浪费。
对于区间修改，有两种方法解决：
- 通过标记永久化，无需下传标记，解决了子节点可能不存在的问题。
- 标记不永久化，下传标记时如果子节点不存在则新开一个子节点。

点击查看代码

void modify(int &k, int l, int r, int p, int q, ll val) {
	if (!k)k = ++cnt;
	t[k].sum += val * (q - p + 1);
	if (p == l && q == r) {
		t[k].lz += val;
		return ;
	}
	int mid = l + r >> 1;
	if (q <= mid) modify(ls, l, mid, p, q, val);
	else if (p > mid) modify(rs, mid + 1, r, p, q, val);
	else modify(ls, l, mid, p, mid, val), modify(rs, mid + 1, r, mid + 1, q, val);
}
ll query(int k, int l, int r, int p, int q, ll lz) {
	if (!k) return 0;
	if (p == l && q == r) return t[k].sum + lz * (r - l + 1);
	int mid = l + r >> 1;
	if (q <= mid) return query(ls, l, mid, p, q, lz + t[k].lz);
	else if (p > mid) return query(rs, mid + 1, r, p, q, lz + t[k].lz);
	else return query(ls, l, mid, p, mid, lz + t[k].lz) + query(rs, mid + 1, r, mid + 1, q, lz + t[k].lz);
}

线段树上二分

一个区间在一个线段树上表现为 \(log\) 个区间，当我们查询的信息在线段树上满足单调性的时候，我们可以利用线段树的结构做到 \(O(log n)\) 复杂度的查询

权值线段树

将数组或集合转化为桶，再以桶构建一棵线段树，这样的线段树我们称为权值线段树。

性质

可以发现，线段树上结点对应的区间 \([l,r]\) 代表了数组或集合中，元素值域在 \([l,r]\) 中的个数。由于元素的范围可能较大，因此权值线段树一般搭配离散化使用。

可持久化数据结构

概念
- 可持久化数据结构总是可以保留每一个历史版本，并且支持操作的不可变特性。
分类
- 部分可持久化：所有版本都可以访问，但是只有最新版本可以修改。
- 完全可持久化：所有版本都既可以访问又可以修改。
实际应用
- 几何计算、字串处理、版本回溯、函数式编程等

可持久化线段树

引题

luoguP3919 【模板】可持久化线段树 1（可持久化数组）
你需要维护一个长度为 n 的数组，支持以下两种操作：
- 在某个历史版本上修改某一个位置上的值
- 访问某个历史版本上的某一位置的值

朴素做法

我们维护 \(m\) 个线段树（本题只是单点修改单点查询，朴素做法使用数组即可），存下来每一个版本的线段树。不难发现空间复杂度是 \(O(nm)\) 的，如何优化？

优化

我们观察两个修改前后的线段树。运用动态开点的思想，单次修改只会改变 \(log n\) 个结点的信息，那么我们直接利用动态开点，将这些点储存到新的结点中，这样既不会破坏原有线段树，又可以存储新的线段树，实现了可持久化。

原理实现

建树

我们用动态开点的方法存储每个点的左右子节点。不过，对于最初版本的那棵树，我们应当一次性建好，而不必一个一个插入。

点击查看代码

void build(int &k, int l, int r) {
	k = ++cnt;
	if (l == r) {
		t[k].val = a[l];
		return ;
	}
	int mid = l + r >> 1;
	build(t[k].ls, l, mid), build(t[k].rs, mid + 1, r);
	...
}

使用时直接调用 \(build(rt[0],1,n)\) 即可

查询

和普通线段树的查询相同，需要注意查哪个版本就选取哪个根节点。
以本题的单点查询为例。

点击查看代码

int query(int k, int l, int r, int pos) {
	if (l == r) return t[k].val;
	int mid = l + r >> 1;
	if (pos <= mid) return query(t[k].ls, l, mid, pos);
	else return query(t[k].rs, mid + 1, r, pos);
}

查询第 \(v\) 个版本的第 \(i\) 个位置调用 \(query(rt[v],1,n,i)\) 即可。

修改

每进行一次单点修改，都会产生一条新的链。我们当前要对第 v 个版本的某一条链进行更新，假设我们已经更新到点 pre。
首先我们要新建一个点 k，代表当前版本对于点 pre 更新后的版本，我们先将 k 的左右儿子指向 pre 的左右儿子，然后再去判断需要的单点修改会在左子树还是右子树上有影响，并递归相应子树即可

点击查看代码

void modify(int &k, int l, int r, int pre, int pos, int val) {
	k = ++cnt, t[k] = t[pre];
	if (l == r) {
		t[k].val = val;
		return ;
	}
	int mid = l + r >> 1;
	if (pos <= mid) modify(t[k].ls, l, mid, t[pre].ls, pos, val);
	else modify(t[k].rs, mid + 1, r, t[pre].rs, pos, val);
}

注意：

可持久化线段树需要动态开点，因此我们需要维护结点的左右子树具体编号。
观察可以发现，可持久化线段树不止有一个根，第 \(i\) 个根代表了第 \(i\) 个版本对应的线段树的根。
在可持久化线段树进行区间修改时，如果不使用标记永久化，则在下传标记时会新建一个结点，这样会导致空间常数较大，因此应尽可能地使用标记永久化。

空间复杂度分析

首先通过动态开点建树，使用了 \(2n − 1\) 个结点，每次修改至多增加\(⌊log2 n⌋ + 1\) 个点，因此总共需要 \(n(⌊log2 n⌋ + 3) − 1\) 个结点，
对于 \(n = 105\) 级别，开 \(30\) 倍足够使用。

可持久化权值线段树

概念

可持久化权值线段树，又称主席树，顾名思义就是将权值线段树可持久化。
由于与权值相关，因此一般搭配离散化使用。
主席树的一个非常经典的应用是静态区间第 K 小。

思考

前面我们在讲线段树上二分时候，已经会在权值线段树上二分求区间 \([1, R]\) 的第 \(k\) 小了。那么我们如何求区间 \([L, R]\) 的第 \(k\) 小呢？

解决方法

利用前缀和的性质，我们只需要有区间 \([1, R]\) 对应的权值线段树，以及区间 \([1, L − 1]\) 对应的权值线段树，在这两棵线段树上一起跑二分，即可实现查询区间 \([L, R]\) 第 \(k\) 小。
因此我们需要维护对于每一个 \(i\)，区间 \([1, i]\) 的权值线段树。
朴素做法是开 \(n\) 个权值线段树，空间复杂度 \(O(n^2log n)\).
我们观察区间 \([1, i]\) 到区间 \([1, i + 1]\) 的变化，相当于在位置 \(i + 1\) 进行了一次单点修改，和上面提到的可持久化线段树一样，因此相邻区间对应的权值线段树只会有一条链是不同的，
因此我们只需要利用可持久化线段树维护这条链即可。空间复杂度 \(O(n log n)\)。

点击查看代码

void modify(int &k, int l, int r, int pre, int pos, int val) {
	k = ++cnt;
	t[k] = t[pre];
	if (l == r) {
		t[k].sum++;
		return ;
	}
	int mid = l + r >> 1;
	if (pos <= mid) modify(t[k].ls, l, mid, t[pre].ls, pos, val);
	else modify(t[k].rs, mid + 1, r, t[pre].rs, pos, val);
	t[k].sum = t[t[k].ls].sum + t[t[k].rs].sum;
}
int query(int p, int q, int l, int r, int rk) {
	if (l == r) return l;
	int mid = l + r >> 1, x = t[t[q].ls].sum - t[t[p].ls].sum;
	if (x >= rk) return query(t[p].ls, t[q].ls, l, mid, rk);
	else return query(t[p].rs, t[q].rs, mid + 1, r, rk - x);
}

posted @ 2025-01-21 09:35 FrankWkd 阅读(88) 评论(0) 收藏举报

刷新页面返回顶部

Loading

FrankWKD

2025dsfz集训Day8：线段树

Day8：线段树

关于线段树

线段树建树

线段树的操作

区间查询

单点修改

相关题目：洛谷P3374 【模板】树状数组 1

将线段树的区间内每个数加上 x：懒标记

个人码风建议

变量与函数

递归与判断

懒标记永久化

线段树的空间复杂度优化

动态开点

线段树上二分

权值线段树

性质

可持久化数据结构

可持久化线段树

引题

朴素做法

优化

原理实现

建树

查询

修改

注意：

空间复杂度分析

可持久化权值线段树

概念

思考

解决方法