字符串Hash学习笔记
以下默认字符串下标从1开始,用 \(s[l,r]\) 表示字符串 \(s\) 的第 \(l\) 到第 \(r\) 个字符组成的子串,记字符串 \(s\) 的长度为 \(len(s)\)。
概述
字符串 \(\text{Hash}\) 常用于各种字符串题目的部分分中。
字符串 \(\text{Hash}\) 可以在 \(O(1)\) 时间内完成判断两个字符串的子串是否相同。通常可以用这个性质来优化暴力以达到骗分的目的。
由于单纯的字符串 \(\text{Hash}\) 已经快成为普及算法了,所以其实现原理不是本文重点。本文重点讲述的是字符串 \(\text{Hash}\) 在 OI 中的常见应用(及各种骗分技巧)
假如你没有听说过字符串 \(\text{Hash}\) ,你可以先学习2年前的洛谷日报哈希基础知识或熟读第一章节。
假如你已经知道了字符串 \(\text{Hash}\) 的基本操作,你可以直接跳过第一章节。
假如你已经精通各种 \(\text{Hash}\) 操作并且随便秒掉字符串的题目,这篇文章大概对您没任何帮助,点个赞再走吧。
一、什么字符串 \(\text{Hash}\)
字符串 \(\text{Hash}\) 其实本质上是一个公式:
其中 \(b,m\) 是常量。
由于 \(s[i]\) 通常是一个字符,你可以直接把ASCII码代入,或者如果是小写字母代入 \(s[i]-'a'\),数字代入 \(s[i]-'0'\) 等等。
比如如果令 \(b=7,m=100,s="114514"\)(此处代入数值,即\(s[1]=1,s[2]=1,s[3]=4,\cdots\))。
那么 \(\text{Hash}(s)=36\),即\((4+1\times7+5\times7^2+4\times7^3+7^4+7^5)\%100\)。
可以发现,我们本质上是将 \(s\) 看成一个 \(b\) 进制数(比如上述例子就是把 \(s\) 看成7进制下的114514)然后 \(\bmod \ p\)。
那为什么要采用这样一个 \(b\) 进制数的形式来处理 \(\text{Hash}\) 呢?
参照哈希表,我们知道如果两个字符串的 \(\text{Hash}\) 值相同,那么这两个串大概率是相同的。
但事实上我们常常需要截取一个字符串的子串。可以发现,对于\(s[l,r]\)这个子串的 \(\text{Hash}\) 值
考虑原串\(s\)的前缀和
于是可以推出:
即
于是对于原串记录\(\text{Hash}\)前缀和,就可以完成 \(O(n)\) 预处理 \(O(1)\) 截取子串 \(\text{Hash}\) 值的优秀时间复杂度。
由于C++的 \(\text{unsigned long long}\) 自带 \(2^{64}\) 的模数和极小的常数,所以一般的情况下,\(\text{Hash}\)运算通常会采用 \(\text{unsigned long long}\),这种写法被称为自然溢出。接下来的代码中默认开头添加:
#define ull unsigned long long
好了,你已经学会了字符串 \(\text{Hash}\) 的所有技巧,让我们来试试吧(雾
二、字符串 \(\text{Hash}\) 的用处
字符串 \(\text{Hash}\) 是一种十分暴力的算法。但由于它能 \(O(1)\) 判断字符串是否相同,所以可以骗取不少分甚至过掉一些字符串题。
接下来先介绍字符串 \(\text{Hash}\) 的一些骗分技巧。
1.字符串匹配(KMP)
这个其实不能说是骗分,毕竟枚举起始点扫一遍 \(O(n)\) 解决,时间复杂度和KMP相同(甚至比KMP短)。
代码略。
2.回文串
考虑以同一个字符为中心的回文串的子串一定是回文串,所以满足可二分性。
将字符串正着和倒着 \(\text{Hash}\) 一遍,如果一个串正着和倒着的 \(\text{Hash}\) 值相等则这个串是回文串。枚举每个节点为回文中心,二分即可。
时间复杂度相比较 \(\text{manacher}\) 较劣,为 \(O(n\log n)\)。发现过不了模板题。
关键代码
ull num[22000000],num2[22000010];
ull find_hash(int l,int r)
{
if(l<=r)
return num[r]-num[l-1]*_base[r-l+1];//顺序Hash
return num2[r]-num2[l+1]*_base[l-r+1];//倒序Hash
}
int l=0,r=min(i-1,len-i);
int len=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(find_hash(i,i+mid)==find_hash(i,i-mid)) l=mid+1,len=mid;//要求顺序Hash与倒序Hash匹配
else r=mid-1;
}
3.\(\text{lcp}\)(最长公共前缀)
\(\text{lcp}\) 也具有可二分性。对于两个串 \(s,t\) 的两个前缀 \(s_1,s_2\),假设 \(len(s_1)<len(s_2)\),若其中 \(s_2\) 是 \(s,t\) 的前缀,则 \(s_1\) 也是 \(s,t\) 的前缀(即公共前缀的前缀一定是公共前缀)。
所以可以在 \(O(\log n)\) 时间求出两个串的前缀。
(这个性质对字符串 \(\text{Hash}\)来讲十分重要,这其实也是字符串 \(\text{Hash}\) 虽然简单但仍能在省选等地方看见的主要因素,具体在后文会讲)
例:后缀排序
仿照上述求 \(\text{lcp}\) 的方式,因为决定两个字符串的大小的是他们 \(\text{lcp}\) 的后一个字符,所以用快排加二分求 \(\text{lcp}\) 即可做到 \(O(n\log^2n)\) 的时间复杂度。比 \(\text{SA}\) 多了一个\(\log\)。
//当然这里是开了O2的,不开直接T飞
ull hashs[1000010];
char str[1000010];
int n;
inline ull get(int l,int r){return hashs[r]-hashs[l-1]*bases[r-l+1];}
bool cmp(int l1,int l2)//二分查找lcp,同时返回下一位的大小
{
int l=-1,r=min(n-l1,n-l2);
while(l<r)
{
int mid=(l+r+1)>>1;
if(get(l1,l1+mid)==get(l2,l2+mid)) l=mid;//判断是否为公共前缀
else r=mid-1;
}
if(l>min(n-l1,n-l2)) return l1>l2;
else return str[l1+l+1]<str[l2+l+1];//返回下一位
}
int a[1000010];
int main()
{
scanf("%s",str+1);
n=strlen(str+1);
bases[0]=1;
for(int i=1;i<=n;i++)
{
bases[i]=bases[i-1]*base;
hashs[i]=hashs[i-1]*base+str[i];
a[i]=i;
}
stable_sort(a+1,a+n+1,cmp);//好像sort被卡常了,stable_sort跑过了
for(int i=1;i<=n;i++) printf("%d ",a[i]);
return 0;
}
除此之外,其实大部分 \(\text{SAM}\) 的题目中都有不少为 \(\text{SA}\) 和 \(\text{Hash}\) 设置的部分分。这里就不列举了。
难道字符串 \(\text{Hash}\) 只能去骗其他算法的分吗?不!其实字符串 \(\text{Hash}\)也有着很多其他算法没有的优点。
1.求字符串的循环节
例:OKR-A Horrible Poem
题意:给定一个字符串,多次询问其某个子串的最短循环节。
可以发现对于字符串串 \(s[l,r]\),如果长度为 \(x\) 的前缀是 \(s[l,r]\) 的一个循环节,则必有 \(len(s[l,r])|x\) 且 \(s[l,r-x]=s[l+x,r]\)
如果存在长度为 \(y\) 的前缀是 \(s\) 的循环节,\(y\) 是 \(x\) 的因数且 \(x\) 是串长的因数,则长度为 \(x\) 的前缀必然是 \(s\) 的循环节(感性理解一下)。
考虑筛出每个数的最大质因数,\(O(\log n)\) 分解质因数,然后从大到小试除,看余下的长度是否是循环节,如果是则更新答案。
char str[N];
int len;
ull hashs[N],bases[N];
void make_hash(void)
{
bases[0]=1;
for(int i=1;i<=len;i++)
{
hashs[i]=hashs[i-1]*base+str[i]-'a'+1;
bases[i]=bases[i-1]*base;
}
}//预处理Hash值
ull get_hash(int l,int r){return hashs[r]-hashs[l-1]*bases[r-l+1];}
int prime[N],nxt[N],cnt;
int num[N],tot;
int main()
{
scanf("%d",&len);
scanf("%s",str+1);
make_hash();
for(int i=2;i<=len;i++)
{
if(!nxt[i]) nxt[i]=prime[++cnt]=i;
for(int j=1;j<=cnt && i*prime[j]<=len;j++)
{
nxt[i*prime[j]]=prime[j];//筛出每个数的最大质因数
if(i%prime[j]==0) break;
}
}
int m;
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int l,r;
scanf("%d%d",&l,&r);
int lens=r-l+1;
int ans=0;
tot=0;
while(lens>1)
{
num[++tot]=nxt[lens];
lens/=nxt[lens];//质因数分解
}
lens=r-l+1;
for(int j=1;j<=tot;j++)
{
int len1=lens/num[j];//进行试除
if(get_hash(l,r-len1)==get_hash(l+len1,r)) lens=len1;//试除成立就取试除后的结果
}
printf("%d\n",lens);
}
return 0;
}
2.动态字符串查询
现在的大多数字符串算法都是静态的查询或者只允许在末尾/开头添加。但如果要求在字符串中间插入或修改,很多算法就无能为力了。
而字符串 \(\text{Hash}\) 的式子是可以合并的,只要知道左区间的 \(\text{Hash}\) 值,右区间的 \(\text{Hash}\) 值,左右区间的大小,就可以 \(O(1)\) 求出总区间的 \(\text{Hash}\) 值。这就使得字符串 \(\text{Hash}\) 可以套上很多数据结构来维护。
一般来说,修改操作中带 插入,可持久化,区间修改 这类字眼的字符串题大多就是 \(\text{Hash}\) 套上一些数据结构或是真·毒瘤题。
例1:火星人
题意:求两个后缀的 \(\text{lcp}\),动态插入字符和改字符。
用平衡树维护区间的 \(\text{Hash}\) 值。仿照上述求 \(\text{lcp}\) 的方法,将上述代码中的 \(\text{get-hash}\) 改为平衡树上查询即可,时间复杂度 \(O(n\log^2n)\)。
关键代码。
inline void update(int u)
{
siz[u]=siz[ch[u][0]]+siz[ch[u][1]]+1;
sum[u]=sum[ch[u][0]]*bases[siz[ch[u][1]]+1]+val[u]*bases[siz[ch[u][1]]]+sum[ch[u][1]];//合并Hash值
}
/*
此处插入你喜欢的平衡树
*/
int main()
{
srand(19260817);
scanf("%s",str+1);
int m;
scanf("%d",&m);
n=strlen(str+1);
bases[0]=1;
for(int i=1;i<=100000;i++) bases[i]=bases[i-1]*base;
for(int i=1;i<=n;i++) root=t.merge(root,t.new_node(str[i]-'a'+1));//平衡树的初始化
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%s%d",opt,&x);
if(opt[0]=='Q')
{
scanf("%d",&y);
printf("%d\n",lcp(x,y));//查询
}
else if(opt[0]=='R')
{
scanf("%s",opt);
t.erase(root,x);
t.insert(root,x-1,opt[0]-'a'+1);//往平衡树中删除
}
else if(opt[0]=='I')
{
scanf("%s",opt);
t.insert(root,x,opt[0]-'a'+1);//往平衡树中插入
n++;
}
}
return 0;
}
例2:The Classic Problem
题目大意:求最短路,其中每条边边权为 \(2^x\),\(n,m,x\leq 10^5\)。
假如不考虑时间复杂度,可以直接高精度加最短路得到 \(O(m\log n\times x)\) 的复杂度。
我们发现这个 \(O(x)\) 是用于 \(+2^x\) 和比较大小的。前者可以用线段树维护,这里不详细说明,可以参考本题题解或是我的博客。
对于后者,我们发现这个可以看成是一个字符串求字典序大小的题。而线段树又恰好可以支持这样的 \(\text{Hash}\) 查询。复杂度 \(O(m\log n\log^2 x)\)。
考虑 \(\text{Hash}\) 求 \(\text{lcp}\) 的本质是二分前缀是否相同,而线段树恰好就满足二分的性质,所以可以从根节点开始,如果两树的右子树的 \(\text{Hash}\) 值不同,可以直接跳右子树继续查询。否则说明右子树相同,跳左子树查询即可。
还有,由于直接复制显然会T,这里的线段树需要可持久化,就是每个节点继承转移节点(最短路树上的父亲)的信息同时加上一次修改。
时间复杂度 \(O(m\log n\log x)\)。
关键代码:
void update(int u,int l,int r)
{
int mid=(l+r)>>1;
hs[u]=hs[ls[u]]+hs[rs[u]]*bs[mid-l+1];//合并Hash值
val[u]=val[ls[u]]==(mid-l+1)?val[ls[u]]+val[rs[u]]:val[ls[u]];//从l开始1的个数
}
int cmp(int u,int v)//比较u,v两树的大小
{
int fu=u,fv=v;
int l=0,r=n;
while(1)
{
if(!u || tag[u]) return fv;//如果有一方全是0,直接跳出
if(!v || tag[v]) return fu;
if(l==r) return hs[u]<=hs[v]?fv:fu;//如果到了叶节点,直接比较
int mid=(l+r)>>1;
if(hs[rs[u]]==hs[rs[v]]) u=ls[u],v=ls[v],r=mid;//如果右子树相同,就比较左子树
else u=rs[u],v=rs[v],l=mid+1;//否则比较右子树
}
}
完整代码详见我的博客。
例三:一道口胡的题(暂时没有找到出处)
题意:维护一个字符串的子串的集合,一开始字符串和集合均为空。
要求完成:在集合中插入一个子串,在字符串末尾加一个字符,求集合中与当前询问的子串 \(\text{lcp}\) 最大值。
比如字符串为 \(abbcbba\)
集合中的子串为 \(s[1,4],s[3,6],s[5,7]\)。
此时查询与子串 \(s[2,5]\),答案为2(\(bbcb\) 和 \(bba\) 的 \(\text{lcp}\) 为2)。
\(m\leq 10^5\),强制在线(为了防止 \(\text{SA}\) 过而特意加的,原题应该没有)。
(假如存在SAM/后缀平衡树的做法可以私信或在下方评论)
首先,考虑一些暴力的做法:
- 暴力将一个子串和集合中的串用上述方法求lcp,时间复杂度 \(O(m^2\log m)\)
- 暴力建\(\text{trie}\),将子串挂到\(\text{trie}\)上,时间复杂度 \(O(m^2)\),空间 \(O(m^2)\)
显然上述的方法都不可行。
考虑使用 \(\text{SA}\) 的想法,与一个串lcp最大的串一定是字典序最靠近它的串,也就是比它字典序大中最小的,和比它小中最大的。
仿照这个思路,使用上述比较两个串字典序大小的方法,考虑使用平衡树来维护子串集合中字典序的顺序,查询时只需查询前驱后继中的 \(\text{lcp}\) 最大值即可。
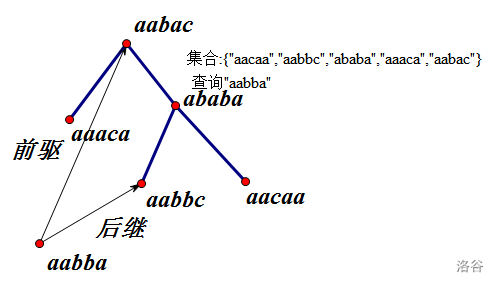
时间复杂度 \(O(m\log^2m)\)
题目都没有,代码肯定咕了
由此可以发现:凡是维护区间,支持维护区间合并(好像区间 \(split\) 也可以)并且支持在线查找的数据结构,诸如什么树套树,树套分块,在线带修莫队,大都可以套上 \(\text{Hash}\) 出道题。
upd:今年ZJOI2020喜闻乐见地出了一道可以用 \(\text{Hash}\) 判断 \(\text{lcp}\) 过的题(虽然用\(\text{SA}\)其实也可以,而且标算其实是一些科技),ZJOI2017也有一道需要用\(\text{Hash}\)的题。
由于上述两题也是利用\(\text{Hash}\)的性质求\(\text{lcp}\),而且主要难度不在于\(\text{Hash}\),所以这里不再阐述。(其实是我太菜了,以上两题都没有过。)
如果以上题目不能满足你的需求,可以参考这份题单
三、字符串的\(\text{Hash}\)冲突与双\(\text{Hash}\)
虽然字符串 \(\text{Hash}\) 在暴力方面有极大的优势,但从它的名字中也可以看出它存在的缺点:\(\text{Hash}\) 冲突。
事实上,自然溢出的 \(\text{Hash}\) 会被定向叉,可以通过构造卡掉,具体可见 Hash Killer I(抱歉,bzoj挂了,链接不见了)
Hash Killer II
题意:卡单 \(\text{Hash}\) 的代码,要求 \(n\leq 10^5\),代码中\(\ mod=10^9+7\)。
upd: bzoj没了,题目也不见了。
根据生日悖论,对于 \(n\) 个不同的字符串,有些 \(mod\) 可能看着比 \(n\) 大得多(比如\(10^9+7\)),但它还是极有可能把其中两个不同的串判成相同。当 \(mod\) 与 \(n\) 相差较大时有冲突概率 \(P\approx 1-(1-\frac{1}{mod})^{\frac{n(n-1)}{2}}\)(具体推导详见百度百科)
通过代入求值可以发现,对于该题,尽管 \(mod\) 是 \(n\) 的1000倍以上,可是这个冲突的概率仍然高得惊人(大概是 \(99.32\%\)),也就是说你随便随机一个字符串上去它大概率就会挂掉。
放一张度娘的图(图中的\(N\)对应题目中的\(mod\))。
upd: 图可能挂了,如果不行请自行百度。
通过式子可以发现,如果想要 \(P\) 不变,\(mod\) 应当与 \(n^2\) 同阶,而不是和 \(n\) 同阶!!(可以理解成:如果我们认为当 \(n=100\) 时, $ mod=10^5$的冲突概率刚好可以接受,那么当 \(n=10^5\) 时就必须要 \(mod\geq10^{11}\)。)
这时候就要用到双 \(\text{Hash}\) 了,其实就是用两个不同的 \(base\) 或是 \(mod\) 对同一个串进行2遍 \(\text{Hash}\) 。
同样,如果两个串第一个 \(\text{Hash}\) 匹配而第二个不匹配,那么这两个串还是不相等(因为相等的串无论怎么 \(\text{Hash}\) 都是相等的)。
所以假如用自然溢出可能会被卡的情况下(其实一般情况下是不会的),建议写双\(\text{Hash}\)。但是需要注意一点,双 \(\text{Hash}\) 的常数十分之大。
我常用的双 \(\text{Hash}\) 写法:
#define ll long long
#define P pair<ll,ll>
#define MP make_pair
#define fi first
#define se second
#define mod 1000000007
P operator +(const P a,const P b){return MP((a.fi+b.fi)%mod,(a.se+b.se)%mod);}
P operator -(const P a,const P b){return MP((a.fi-b.fi+mod)%mod,(a.se-b.se+mod)%mod);}
P operator *(const P a,const P b){return MP(a.fi*b.fi%mod,a.se*b.se%mod);}
const P base=MP(233,2333);
//后续代码同单Hash
不过,双 \(\text{Hash}\) 其实很不常用,首先它的误判率并不比自然溢出的写法优秀,再加上其巨大的常数,更长的代码量,\(pair\) 类型也并不如 \(ull\) 那么友好,所以绝大部分 \(\text{Hash}\) 用的都还是自然溢出。
当然,在codeforces上写自然溢出的绝对是勇士(别问我怎么知道的。
四、总结
虽然字符串 \(\text{Hash}\) 相比较其他字符串算法而言存在一定概率出错。这在计数题(尤其是数据打包的题目)中有时是十分致命的(虽然是极小的概率)。
但是字符串 \(\text{Hash}\) 的一些优秀性质也使得它有其他算法所没有的一些优势。在多数题目中,字符串 \(\text{Hash}\) 也未尝不是一种简易的骗分方式。
当然,大多数情况下 \(\text{Hash}\) 都是配合其他算法以及数据结构一起出现的,所以就算会了Hash我还是咸鱼。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号