斜率优化 DP

斜率优化DP

在单调队列优化过程中，转移方程被拆成了两部分，第一部分仅与 $j$ 有关，而另一部分仅与 $i$ 有关，因此我们可以利用单调队列仅维护与 $j$ 有关的部分，实现问题的快速求解。

但仍然有很多转移方程，$i$ 和 $j$ 是紧密相关的，这个时候单调队列优化就不适用了，例如如下转移方程格式：

\[y[j] = x[j] \times k[i]+dp[i]+base[i] \]

其中 $x[j]$ 与 $y[j]$ 是一个仅与 $j$ 以及 $dp[j]$ 有关的式子，不受 $i$ 影响；而 $k[i]$ 与 $base[i]$ 则是一个仅与 $i$ 有关的式子，不受 $j$ 影响。因此这个式子的唯一未知量就是 $dp[i]$，如何选择合适的 $j$ 来求取最优的 $dp[i]$ 就是该转移方程的关键问题。

仔细观察上述式子，不难发现其实这是一个形如 $y=kx+b$ 的式子，$k$ 由 $i$ 决定，而 $x$ 和 $y$ 则由 $j$ 决定，因此我们可以将这个问题抽象为，平面上有很多个点 $(x[j] , y[j])$，然后我们用斜率为 $k[i]$ 的直线去靠近这些点，希望找一个使 $b$ 最大的 $j$。

而这种情况下，我们就需要维护上/下凸壳，且需要根据具体的题意，如 $k[i]$ 是否递增，$k[i]$ 是否始终为正，$k[i]$ 是否有可能为负等问题来选择具体的维护和转移方法，可能会涉及 set 以及二分的使用。
总结一下，在斜率优化问题中，每一个 $j$ 都是一个二维平面上的点 $(x[j], y[j])$，转移时我们需要用斜率为 $k[i]$ 的直线来靠近这些点，使得 $b[i]$ 达到最优。

trick:

斜率单调暴力移指针

斜率不单调二分找答案

$x$ 坐标单调开单调队列

$x$ 坐标不单调或两者均不单调开平衡树或 cdq 分治

建议可以先看最后的“一些常见问题”。

P3195 [HNOI2008] 玩具装箱

题目大意：

共有 $n$ 个玩具，第 $i$ 个玩具长度为 $c_i$，如果将第 $i$ 个玩具到第 $j$ 个玩具放到一个容器中，则该容器长度 $x=j-i+\sum_{k=i}^jc_k$。制作一个容器的费用为 $(x-L)^2$，其中 $L$ 为常数，可以制作若干个容器。求将所有玩具都放入容器中的费用最小值。

$n\leq 5\times 10^4,1\leq L,c_i\leq10^7$

考虑朴素 DP：

令 $dp[i]$ 表示第 $i$ 个玩具被装起来后的总费用最小值，$sum[i]$ 表示前 $i$ 个玩具长度之和。可得转移方程：

\[dp[i] = \min\{dp[j]+(sum[i]-sum[j]+(i-j-1)-L)^2\} \quad (j < i) \]

$i$ 制作完从 $j$ 制作完转移而来，新容器装的玩具实际是 $[j+1, i]$。

时间复杂度为 $O(n^2)$，运气好可能能过。

考虑优化：

将后面改写成一段只与 $i$ 有关，一段只与 $j$ 有关。令 $a[i] = sum[i]+i, b[i] = sum[j]+j+L+1$。

则（先省略 $\min$）

\[dp[i] = dp[j]+(a[i]-b[j])^2 \]

平方难以优化，展开得

\[dp[i] = dp[j]+a[i]^2-2\cdot a[i]\cdot b[j]+b[j]^2 \]

有点斜率优化的影子了，移项得

\[dp[j]+b[j]^2 = 2\cdot a[i]\cdot b[j] + dp[i] - a[i]^2 \]

将 $dp[j]+b[j]^2$ 看作 $y[j]$，$b[j]$ 看作 $x[j]$，$2\cdot a[i]$ 看作 $k[i]$，对于每个 $i$ 来说，$-a[i]^2$ 和 $2\cdot a[i]$ 都是确定的，式子可写作

\[y[j] = k[i]\times x[j]+dp[i]+base[i] \]

接下来就是求解。

$dp[i]$ 的含义转化为当上述直线过点 $P(b[j], dp[j]+b[j]^2)$ 时，直线在 $y$ 轴的截距加上 $a[i]^2$（对 $i$ 来说是一个定值）的最小值。所以找到可能直线的截距的最小值就行了。

因此，类似线性规划，我们将这条直线从下往上平移，直到过第一个符合要求的点时停下，此时截距即为最小。

画出图像如下（红色为目标直线）：

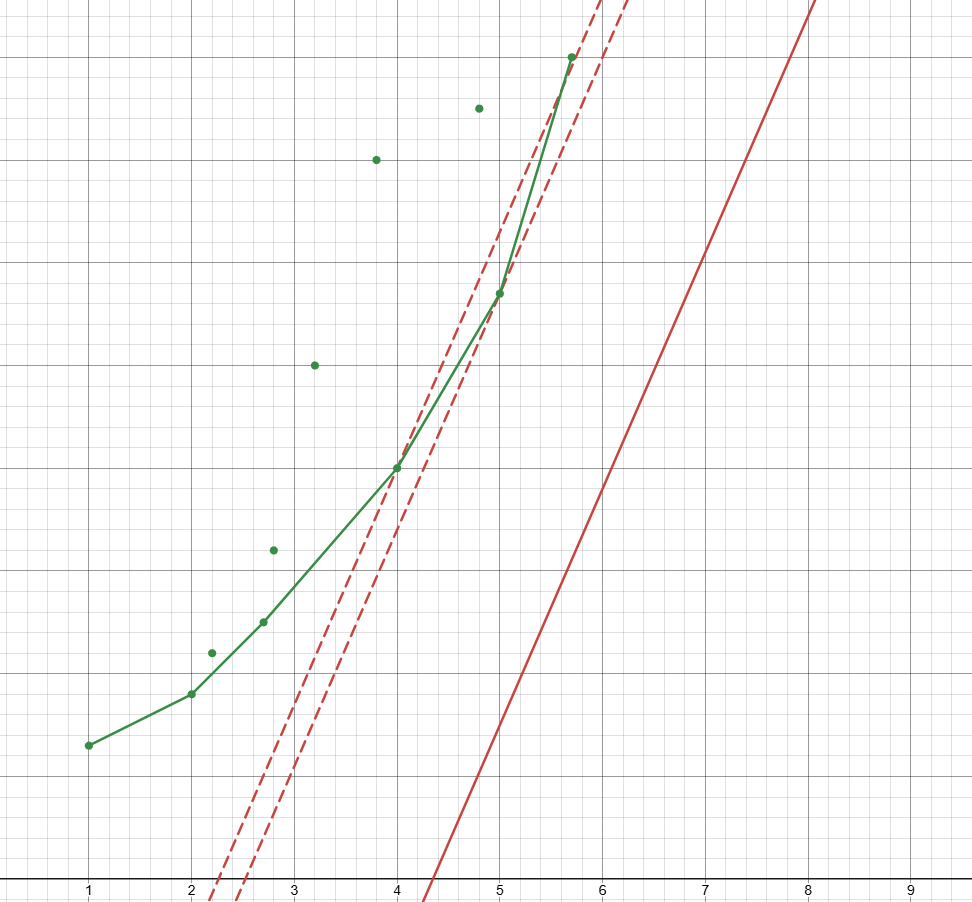
结合图像分析可知，本题中可能为最优的 $P$ 点（图中用直线连接）组成了一个下凸包。

显然，凸包中相邻两点斜率是单调递增的。

而目标直线的斜率 $2 \cdot a[i]$ 随 $i$ 也是单调递增的。

令 $A, B$ 两点之间斜率为 $slope(A, B)$。由图像易知，满足条件的第一个 $P_j$ 即为第一个 $slope(P_j, P_{j+1}) > 2\cdot a[i]$ 的点。

因为凸包和直线斜率均递增，我们可以用单调队列来维护这个凸包：

设队首为 $head$，队尾为 $tail$。需要让队首元素为最优的 $P_j$ 的下标 $j$。

对队首：

队首元素一直右移直到满足 $slope(P_{head},P_{head+1})\ge 2\cdot a[i]$。

解释：如果 $slope(P_{head},P_{head+1}) < 2\cdot a[i]$，显然 $P_j$ 不是最优。可直接删去，因为目标直线斜率单调递增，所以当前删去的 $P_j$ 一定对之后的 $dp[i]$ 也不是最优，不会造成影响。
此时队首的点即为最优，根据它计算得出 $dp[i]$。
对队尾：

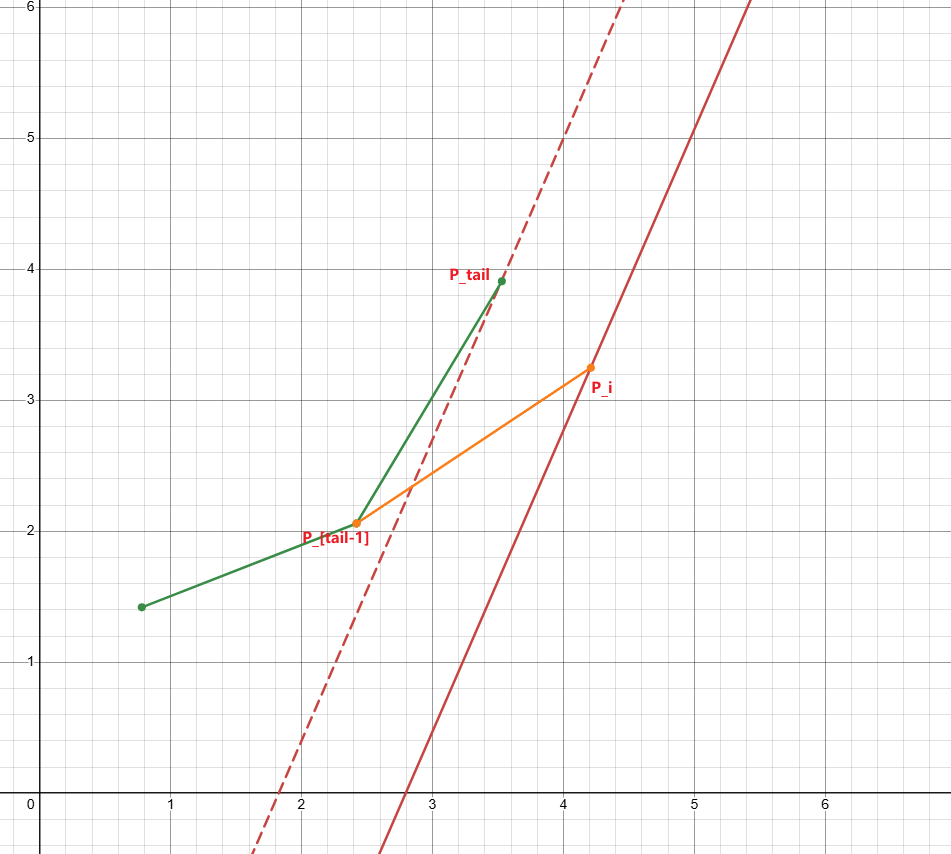
队尾元素一直左移直到满足 $slope(P_{tail-1},P_{tail})\le slope(P_{tail-1},P_i)$。

解释：如果 $slope(P_{tail-1},P_{tail}) > slope(P_{tail-1},P_i)$，说明 $P_{tail}$ 在凸包内部，一定没有 $P_i$ 优，因此可以删去。
在队尾插入 $P_i$。

最后注意初始化时要加入单调队列的点为 $P_0$ 而不是 $P_1$，否则就变成了第一个物品必须单独装。

朴素前缀和优化 DP 代码：

Code

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
const int N = 5e4+5;

ll c[N], sum[N];
ll dp[N]; // dp[i] 表示装完第 i 个玩具后所需费用的最小值

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, L; cin>>n>>L;
    for(int i=1; i<=n; i++){
        cin>>c[i];
        sum[i] = sum[i-1]+c[i];
    }
    for(int i=1; i<=n; i++)
        dp[i] = INT64_MAX;
    for(int i=1; i<=n; i++){
        for(int j=0; j<i; j++){
            dp[i] = min(dp[i], dp[j]+(sum[i]+i-sum[j]-j-1-L)*(sum[i]+i-sum[j]-j-1-L)); // [j+1, i]
        }
    }
    cout<<dp[n];
    return 0;
}

正解加上斜率优化 DP 代码：

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
#define db double
const int N = 5e4+5;

int n, L;
ll c[N], sum[N];
ll Q[N], dp[N]; // dp[i] 表示装完第 i 个玩具后所需费用的最小值

db a(int x){return sum[x]+x;}
db b(int x){return a(x)+L+1;}
db X(int x){return b(x);}
db Y(int x){return (db)dp[x]+b(x)*b(x);}
db slope(int a, int b){return (Y(a)-Y(b))/(X(a)-X(b));}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin>>n>>L;
    for(int i=1; i<=n; i++){
        cin>>c[i];
        sum[i] = sum[i-1]+c[i];
    }
    int head = 1, tail = 0;
    Q[++tail] = 0;
    for(int i=1; i<=n; i++){
        while(head<tail && slope(Q[head], Q[head+1])<=2*a(i)) head++;
        dp[i] = dp[Q[head]]+(a(i)-b(Q[head]))*(a(i)-b(Q[head]));
        while(head<tail && slope(i, Q[tail-1])<=slope(Q[tail], Q[tail-1])) tail--;
        Q[++tail] = i;
    }
    cout<<dp[n];
    return 0;
}

P5017 [NOIP2018 普及组] 摆渡车

题目大意：

有 $n$ 名同学要乘车从 A 地前往 B 地，第 $i$ 位同学在第 $t_i$ 分钟去等车。只有一辆车在工作，但车容量可以视为无限大。车往返一趟总共花费 $m$ 分钟（同学上下车时间忽略不计）。车要将所有同学都送到 B 地。如果能任意安排车出发的时间，那么这些同学的等车时间之和最小为多少呢？

注意：车回到 A 地后可以即刻出发。

$n\leq500,m\leq100,0\leq t_i\leq4\times10^6$

我们不妨认为时间是一条数轴，每名同学按照到达时刻分别对应数轴上可能重合的点。安排车辆的工作，等同于将数轴分成若干个左开右闭段，每段的长度 $\ge m$。原本的等车时间之和，自然就转换成所有点到各自所属段右边界的距离之和。

令 $dp[i]$ 表示 $i$ 时刻前（包括 $i$）所有人的最小等待时间。可得：

\[dp[i] = \min_{j \le i-m}\{dp[j] + \sum_{k=j+1}^{i}(i-t[k])\} \]

以上算的是 $(j, i]$ 段的贡献。观察到 $t_i$ 可能等于 $0$，所以还需特判 $[0, i]$ 单独作为一段的边界情况，即 $dp[i] = \sum\limits_{k\le i}(i-t_k)$。

考虑前缀和优化求和部分：

\[\sum_{j<k\le i}(i-t[k])=(\sum_{j<k\le i}i)-(\sum_{j<k\le i}t[k])=(cnt[i]-cnt[j])\times i-(sum[i]-sum[j]) \]

其中 $cnt[i]$ 表示 $[0, i]$ 中的人数，$sum[i]$ 表示 $[0, i]$ 中的人的到达时间总和。

至此，时间复杂度为 $O(t^2)$，可得 50pts。

考虑剪去无用转移：

\[dp[i] = \min_{i-2m < j \le i-m}\{dp[j] + (cnt[i]-cnt[j])\times i-(sum[i]-sum[j])\} \]

显然 $i-2m$ 前的最优方案已经转移到了 $(i-2m, i-m]$ 上。

考虑剪去无用状态：

假设正在求 $dp[i]$，但在 $(i-m,i]$ 中没有任何多出来的人，那么这个 $dp[i]$ 相对来说就是无用的（中间没有任何贡献），继承上一次 $i-m$ 的 $dp$ 值即可。

可以证明有用的位置 $\le nm$ 个。至此，时间复杂度为 $O(nm^2+t)$，可得 100pts。

因为我们要讲斜率优化 DP，所以我们要讲斜率优化 DP：

从前缀和优化后的式子开始，将括号拆开得

\[dp[i] = dp[j]+cnt[i]\times i-cnt[j]\times i-sum[i]+sum[j] \]

移项得

\[dp[j]+sum[j] = i\times cnt[j] + sum[i] - i\times cnt[i] + dp[i] \]

将 $dp[j]+sum[j]$ 看作 $y[j]$，$cnt[j]$ 看作 $x[j]$，$i$ 看作 $k[i]$，对于每个 $i$ 来说，$sum[i]-i\times cnt[i]$ 是确定的，式子可写作

\[y[j] = k[i]\times x[j]+dp[i]+base[i] \]

斜率 $i$ 单调上升，维护下凸壳。对于 $i$ 把 $i-m$ 推入队列，即可保证决策点 $j\le i-m$。

每个状态点最多进出队列一次，时间复杂度 $O(t)$。

还有一个小小的优化，考虑可从 $t=0$ 转移而来而不用特判，只要将所有时间值向右偏移 $1$ 即可。

朴素前缀和优化 DP 代码：

Code

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
constexpr int N = 10005;

int dp[N]; // dp[i] 表示 i 时刻前所有人的最小等待时间
int cnt[N], sum[N], t;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, m; cin>>n>>m;
    for(int i=1; i<=n; i++){
        int ti; cin>>ti;
        t = max(t, ti);
        cnt[ti]++;
        sum[ti] += ti;
    }
    for(int i=1; i<t+m; i++){
        cnt[i] += cnt[i-1];
        sum[i] += sum[i-1];
    }
    for(int i=0; i<t+m; i++){
        dp[i] = cnt[i]*i-sum[i];
        for(int j=0; j<=i-m; j++){
            dp[i] = min(dp[i], dp[j]+(cnt[i]-cnt[j])*i-(sum[i]-sum[j]));
        }
    }
    int ans = 1e9;
    for(int i=t; i<t+m; i++)
        ans = min(ans, dp[i]);
    cout<<ans;
    return 0;
}

剪枝优化后代码：

Code

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
constexpr int N = 4e6+5;

int dp[N]; // dp[i] 表示 i 时刻前所有人的最小等待时间
int cnt[N], sum[N], t;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, m; cin>>n>>m;
    for(int i=1; i<=n; i++){
        int ti; cin>>ti;
        t = max(t, ti);
        cnt[ti]++;
        sum[ti] += ti;
    }
    for(int i=1; i<t+m; i++){
        cnt[i] += cnt[i-1];
        sum[i] += sum[i-1];
    }
    for(int i=0; i<t+m; i++){
        if(i>=m && cnt[i]==cnt[i-m]){
            dp[i] = dp[i-m];
            continue;
        }
        dp[i] = cnt[i]*i-sum[i];
        for(int j=max(0, i-m-m+1); j<=i-m; j++){
            dp[i] = min(dp[i], dp[j]+(cnt[i]-cnt[j])*i-(sum[i]-sum[j]));
        }
    }
    int ans = 1e9;
    for(int i=t; i<t+m; i++)
        ans = min(ans, dp[i]);
    cout<<ans;
    return 0;
}

斜率优化后代码：

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
#define db long double
constexpr int N = 4e6+5;

int dp[N]; // dp[i] 表示 i 时刻前所有人的最小等待时间
int cnt[N], sum[N], t;
int Q[N], head = 1, tail = 0;

db X(int x){return cnt[x];}
db Y(int x){return (db)dp[x]+(db)sum[x];}
db slope(int a, int b){return X(a)==X(b) ? (Y(b)>Y(a)?1e9:-1e9) : (Y(a)-Y(b))/(X(a)-X(b));}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, m; cin>>n>>m;
    for(int i=1; i<=n; i++){
        int ti; cin>>ti; ti++; // +1 使 t=0 可转移而来
        t = max(t, ti);
        cnt[ti]++;
        sum[ti] += ti;
    }
    for(int i=2; i<t+m; i++){
        cnt[i] += cnt[i-1];
        sum[i] += sum[i-1];
    }
    Q[++tail] = 0;
    for(int i=1; i<t+m; i++){
        if(i>m){ // 先判断可不可以由 i-m 转移
            while(head<tail && slope(Q[tail-1], Q[tail])>=slope(Q[tail-1], i-m)) tail--; // tip1:两个点才能操作 tip2:等于号去重防止分母出锅
            Q[++tail] = i-m;
        }
        while(head<tail && slope(Q[head], Q[head+1])<=i) head++;
        dp[i] = dp[Q[head]]+cnt[i]*i-cnt[Q[head]]*i-sum[i]+sum[Q[head]];
    }
    int ans = 1e9;
    for(int i=t; i<t+m; i++)
        ans = min(ans, dp[i]);
    cout<<ans;
    return 0;
}

P5785 [SDOI2012] 任务安排

题目大意：

$n$ 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 $n$ 个任务可以被分成若干批，每批包含相邻的若干任务。

从零时刻开始，这些任务被分批加工，第 $i$ 个任务单独完成所需的时间为 $t_i$。在每批任务开始前，机器需要启动时间 $s$，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。

每个任务的费用是它的完成时刻乘以一个费用系数 $c_i$。请确定一个分组方案，使得所有任务总费用最小。

$1 \le n \le 3 \times 10^5$，$1 \le s \le 2^8$，$ \left| T_i \right| \le 2^8$，$0 \le C_i \le 2^8$。

设 $dp[i]$ 表示完成到以第 $i$ 个任务为结束任务时所花费的最短时间。

每次开机对当前任务 $j$ 后的任务都会造成影响，所以每次开机后总费用直接加上 $s \times \sum\limits_{k=j+1}^{n}c_k$ 即可。

这批任务的完成费用就是当前任务 $i$ 前的所有任务时间总和乘 $[j+1, i]$ 中每个任务的费用系数，即 $(\sum\limits_{k=1}^{i}t_k) \times (\sum\limits_{k=j+1}^{i}c_k)$。

设 $st[i]$ 为任务需要时间的前缀和，$sc[i]$ 为任务费用系数的前缀和。得

\[dp[i] = \min_{j<i}\{dp[j]+s\times (sc[n]-sc[j])+st[i]\times (sc[i]-sc[j])\} \]

至此，时间复杂度为 $O(n^2)$。

接下来省略 $\min$，将式子拆开得

\[dp[i] = dp[j]+s\times sc[n]-s\times sc[j]+st[i]\times sc[i]-st[i]\times sc[j] \]

移项得

\[dp[j]-s\times sc[j] = st[i]\times sc[j]-st[i]\times sc[i]-s\times sc[n]+dp[i] \]

将 $dp[j]-s\times sc[j]$ 看作 $y[j]$，$sc[j]$ 看作 $x[j]$，$st[i]$ 看作 $k[i]$，对于每个 $i$ 来说，$-st[i]\times sc[i]-s\times sc[n]$ 是确定的，式子可写作

\[y[j] = k[i]\times x[j]+dp[i]+base[i] \]

因为 $t_i$ 可能小于 $0$，所以 $k_i$ 不单调，此时需要用二分来寻找最接近的 $k$ 值。如下图所示：

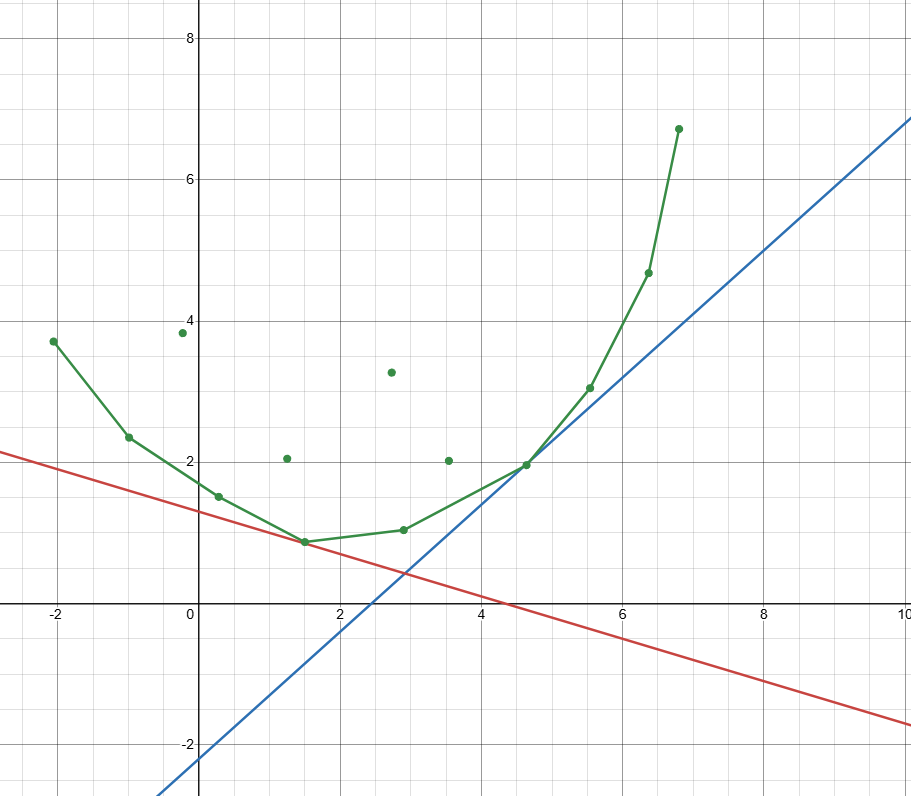
询问的斜率可能先是蓝色的直线，再是红色的直线。所以要用队列维护一个下凸包，然后二分查找。

朴素前缀和优化 DP 代码：

Code

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
const int N = 3e5+5;

ll st[N], sc[N];
ll dp[N]; // dp[i] 表示完成第 i 个任务后的最小费用值

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n, s; cin>>n>>s;
    for(int i=1; i<=n; i++){
        cin>>st[i]>>sc[i];
        st[i] += st[i-1];
        sc[i] += sc[i-1];
    }
    memset(dp, 0x3f, sizeof(dp));
    dp[0] = 0;
    for(int i=1; i<=n; i++){
        for(int j=0; j<i; j++){
            dp[i] = min(dp[i], dp[j]+s*(sc[n]-sc[j])+st[i]*(sc[i]-sc[j]));
        }
    }
    cout<<dp[n];
    return 0;
}

斜率优化 DP 代码：

#include<bits/stdc++.h>
using namespace std;
#define DEBUG(a) cout<<"Dline[ "<<__LINE__<<" ]: "<<(a)<<"\n";
#define ll long long
const int N = 3e5+5;

ll st[N], sc[N];
ll dp[N], s; // dp[i] 表示完成第 i 个任务后的最小费用值
ll Q[N], head = 1, tail = 0;

ll X(ll x){return sc[x];}
ll Y(ll x){return dp[x]-s*sc[x];}

ll Search(ll l, ll r, ll k){
    ll res = 0;
    while(l<=r){
        ll mid = (l+r)>>1;
        if(Y(Q[mid+1])-Y(Q[mid]) < k*(X(Q[mid+1])-X(Q[mid]))){
            l = mid+1;
        } else{
            res = mid;
            r = mid-1;
        }
    }
    return Q[res];
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n; cin>>n>>s;
    for(int i=1; i<=n; i++){
        cin>>st[i]>>sc[i];
        st[i] += st[i-1];
        sc[i] += sc[i-1];
    }
    Q[++tail] = 0;
    for(int i=1; i<=n; i++){
        int j = Search(head, tail, st[i]);
        dp[i] = dp[j]+s*(sc[n]-sc[j])+st[i]*(sc[i]-sc[j]);
        while(head<tail && (__int128)(Y(Q[tail])-Y(Q[tail-1]))*(X(i)-X(Q[tail-1])) >= (__int128)(Y(i)-Y(Q[tail-1]))*(X(Q[tail])-X(Q[tail-1]))) tail--;
        // 这里写成 (Y(Q[tail])-Y(Q[tail-1]))*(X(i)-X(Q[tail])) >= (Y(i)-Y(Q[tail]))*(X(Q[tail])-X(Q[tail-1])) 却不会爆 ll，即使两者是等价的
        Q[++tail] = i;
    }
    cout<<dp[n];
    return 0;
}

P3648 [APIO2014] 序列分割

题目大意：

你正在玩一个关于长度为 $n$ 的非负整数序列 $a$ 的游戏。这个游戏中你需要把序列分成 $m + 1$ 个非空的块。为了得到 $m + 1$ 块，你需要重复下面的操作 $m$ 次：

选择一个有超过一个元素的块（初始时你只有一块，即整个序列）。
选择两个相邻元素把这个块从中间分开，得到两个非空的块。

每次操作后你将获得那两个新产生的块的元素和的乘积的分数。你想要最大化最后的总得分。

$2 \leq n \leq 10^5, 1 \leq m \leq \min\{n - 1, 200\}, 0 \le a_i \le 10^4$。

首先，这题最重要的是发现一个性质：答案与切的顺序无关。

证明：考虑将一块序列 $abc$ 分为 $a, b, c$ 三块。

方法一：先分成 $a, bc$。答案为 $a(b+c)+bc=ab+ac+bc$。

方法二：先分成 $ab, c$。答案为 $ab+(a+b)c=ab+ac+bc$。

接下来就可以考虑 dp 了，设 $dp[i][k]$ 表示前 $i$ 个数切 $k$ 刀得到的最大得分，$s[i]$ 表示前 $i$ 个数的元素和。

\[dp[i][k] = \max_{j<i}\{dp[j][k-1]+s[j]\times (s[i]-s[j])\} \]

至此，时间复杂度为 $O(n^2k)$，可得 50pts。

考虑如何进行斜率优化：

问题在于多了一个参数 $k$，发现 $k$ 只与 $k-1$ 有关，可以用滚动数组存，设 $g[i]$ 表示前 $i$ 个数切 $k-1$ 刀得到的最大的分，可得

\[dp[i] = \max_{j<i}\{g[j]+s[j]\times (s[i]-s[j])\} \]

拆开得

\[dp[i] = g[j]+sum[j]\times sum[i]-sum[j]^2 \]

移项得

\[g[j]-sum[j]^2 = -sum[i]\times sum[j]+dp[i] \]

将 $g[j]-sum[j]^2$ 看作 $y[j]$，$sum[j]$ 看作 $x[j]$，$-sum[i]$ 看作 $k[i]$，式子可写作

\[y[j] = k[i]\times x[j]+dp[i] \]

$k[i]$ 单调递减，$x[j]$ 单调递增。结合求 $dp[i]$ 的最大值来看，这里我们应该维护一个上凸包。队头元素代表的下标就是分割的点。

时间复杂度为 $O(nk)$，可得 100pts。

朴素前缀和优化 DP 代码 & 滚动数组后代码：

Code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+5;

ll dp[N][205]; // dp[i][j] 表示前 i 个数切 j 刀的最大总得分
ll sum[N];
int fa[N][205];

int main(){
	int n, m; cin>>n>>m;
	for(int i=1; i<=n; i++){
		cin>>sum[i];
		sum[i] += sum[i-1];
	}
	for(int i=1; i<=n; i++){
		for(int k=1; k<=min(m, i-1); k++){
			for(int j=0; j<i; j++){
				if(dp[i][k] <= dp[j][k-1]+sum[j]*(sum[i]-sum[j])){
					dp[i][k] = dp[j][k-1]+sum[j]*(sum[i]-sum[j]);
					fa[i][k] = j;
				}
			}
		}
	}
	cout<<dp[n][m]<<"\n";
	for(int i=fa[n][m]; m; i=fa[i][--m])
		cout<<i<<" ";
	return 0;
}









#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+5;

ll dp[N]; // dp[i] 表示前 i 个数切 j 刀的最大总得分
ll g[N]; // g[i] 表示前 i 个数切 j-1 刀的最大总得分
ll sum[N];
int fa[N][205];

int main(){
	int n, m; cin>>n>>m;
	for(int i=1; i<=n; i++){
		cin>>sum[i];
		sum[i] += sum[i-1];
	}
	for(int k=1; k<=min(m, n-1); k++){
		for(int i=1; i<=n; i++)
			g[i] = dp[i];
		for(int i=k; i<=n; i++){
			for(int j=0; j<i; j++){
				if(dp[i] <= g[j]+sum[j]*(sum[i]-sum[j])){ // 可能出现最优解为 0 的可能，所以是 <= ' in:2 1 0 123 out:0 1
					dp[i] = g[j]+sum[j]*(sum[i]-sum[j]);
					fa[i][k] = j;
				}
			}
		}
	}
	cout<<dp[n]<<"\n";
	for(int i=fa[n][m]; m; i=fa[i][--m])
		cout<<i<<" ";
	return 0;
}

斜率优化 DP 代码：

#include<bits/stdc++.h>
#define ll long long
#define db long double
using namespace std;
const int N = 1e5+5;

ll dp[N]; // dp[i] 表示前 i 个数切 j 刀的最大总得分
ll g[N]; // g[i] 表示前 i 个数切 j-1 刀的最大总得分
ll sum[N];
ll Q[N], head = 1, tail = 0;
int fa[N][205];

ll Y(int x){return g[x]-sum[x]*sum[x];}
ll X(int x){return sum[x];}
db slope(int a, int b){return X(a)==X(b) ? (Y(b)>=Y(a)?1e18:-1e18) : (Y(b)-Y(a))/(db)(X(b)-X(a));}

int main(){
	int n, m; cin>>n>>m;
	for(int i=1; i<=n; i++){
		cin>>sum[i];
		sum[i] += sum[i-1];
	}
	for(int k=1; k<=min(m, n-1); k++){
		for(int i=1; i<=n; i++)
			g[i] = dp[i];
        head = 1, tail = 0;
        Q[++tail] = 0;
		for(int i=k; i<=n; i++){
			while(head<tail && slope(Q[head], Q[head+1])>=(-sum[i])) head++;
            dp[i] = g[Q[head]]+sum[Q[head]]*(sum[i]-sum[Q[head]]);
            fa[i][k] = Q[head];
            while(head<tail && slope(Q[tail-1], Q[tail])<=slope(Q[tail-1], i)) tail--;
            Q[++tail] = i;
		}
	}
	cout<<dp[n]<<"\n";
	for(int i=fa[n][m]; m; i=fa[i][--m])
		cout<<i<<" ";
	return 0;
}

一些常见问题

$1$. 写出 dp 方程后，要先判断能不能使用斜优，即是否存在 $function(i)\times function(j)$ 的项或者 $\frac{Y(j)-Y(j^{\prime})}{X(j)-X(j^{\prime})}$ 的形式。

$2$. 通过大小于符号或者 $b$ 中 $dp[i]$ 的符号结合题目要求 $\min/\max$ 判断是上凸包还是下凸包，不要见一个方程就直接盲猜一个下凸。

$3^{\ast}$. 当 $X(j)$ 非严格递增时，在求斜率时可能会出现 $X(j_1)=X(j_2)$ 的情况，此时最好是写成这样的形式：return Y(j)>=Y(i) ? inf : -inf，而不要直接返回 inf 或者 -inf，在某些题中情况较复杂，如果不小心画错了图，返回了一个错误的极值就完了，而且这种错误只用简单数据还很难查出来。

$4^{\ast}$. 注意比较 $k_0[i]$ 和 $slope(j_1,j_2)$ 要写规范，要用右边的点减去左边的点进行计算（结合第 3 点来看，可防止返回错误的极值）。

$5^{\ast}$. 队列初始化大多都要塞入一个点 $P(0)$，例如玩具装箱，需要塞入 $P(b[0], dp[0]+b[0]^2)$，即 $P(0,0)$，其代表的决策点为 $j=0$。

$6^{\ast}$. 手写队列的初始化是 head=1, tail=0，由于塞了初始点导致 $tail$ 加 $1$，所以在一些题解中可以看到 head=tail=1 甚至是 head=t=0, head=tail=2 之类的写法，其实是因为省去了塞初始点的代码。它们都是等价的。

$7^{\ast}$. 手写队列判断不为空的条件是 head <= tail，而出入队判断都需要有至少两个元素才能进行操作。所以应是 head < tail。

$8^{\ast}$. 计算斜率可能会因为向下取整而出现误差，所以 $slope$ 函数最好设为 long double 类型。当然，也可以用斜率交叉相乘的方式来比较，这样精确度更高，且包括第 3 点，但是可能会爆 long long。

$9$. 有可能会有一部分的 dp 初始值无法转移过来，需要手动提前弄一下，例如摆渡车。

$10^{\ast}$. 在比较两个斜率时，尽量写上等于，即 $\le$ 和 $\ge$ 而不是 $<$ 和 $>$。这样写对于去重有奇效（有重点时会导致斜率分母出锅），但不要以为这样就可以完全去重，因为要考虑的情况可能会非常复杂，所以还是推荐加上第 3 点中提到的特判，确保万无一失。

$11^{\ast}$. 在判断可删图形时有两种方法(以下凸包为例)，一种是 slope(Q[tail-1],Q[tail])<=slope(Q[tail],i)，另一种是 slope(Q[tail-1],Q[tail])<=slope(Q[tail-1],i)，都表示出现了可以删去点 $Q[tail]$ 的情况 (只要对边界、去重的处理足够严谨，两种写法是没有区别的)。

参考资料

【学习笔记】动态规划—斜率优化DP（超详细）

DP 转移方程 —— 单调队列优化 & 斜率优化 & 李超树优化

等等

posted @ 2024-10-05 08:36 FlyPancake 阅读(64) 评论(1) 收藏举报

刷新页面返回顶部

FlyPancake

斜率优化 DP

斜率优化DP

P3195 [HNOI2008] 玩具装箱

P5017 [NOIP2018 普及组] 摆渡车

P5785 [SDOI2012] 任务安排

P3648 [APIO2014] 序列分割

一些常见问题

参考资料

公告