c++递归函数

一、什么是递归算法

　　　递归即递推+回归。递归算法是把问题转化为规模缩小了的同类子问题，然后递归调用函数（或过程）来表示问题的解。

二、递归算法的特点

　　1.必须有 递归函数 + 递归出口

　　2.递归算法解题通常显得简洁，但效率较低且系统通过栈来储存每一层的返回点、局部变量，递归次数过多容易造成栈溢出。

三、如何编写递归函数

　　例：Hanoi 塔（问题内容不再赘述）

　　　　我们以三个圆盘（从小到大依次成为1，2，3号）三根柱子（A,B,C)为例: 

 　　　　

　　

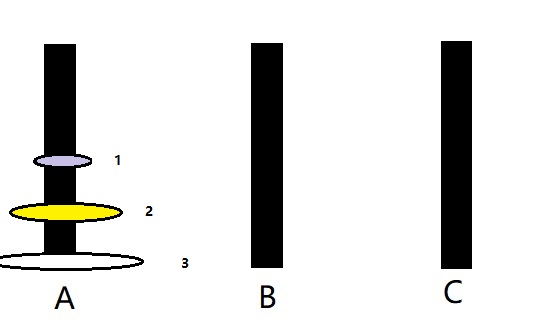
　　　　想要将 3号 移至C柱

　　　　　　 step1.　　借助C把1、2号盘移到B;　　　　　　

　　　　　　 step2.　　将3号盘移至C;　　

　　　　

 

 

 

 

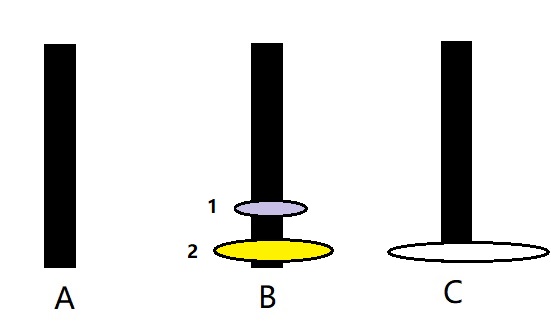
　　　　　想要将 2号  移至 C 柱 则用上述同样的思想     (递归函数的内涵所在,将大问题逐个分解为相同小问题）

　　　　　 　  step1. 借助C 将 1号盘 移至 A柱　/*这里可以直接将 1号盘移至A,但如果 B盘上不止一个盘则需要借助C ,我这里是 按整体规律来写*/

 　　　　  　      step2.  将 2号盘 移至 C;

　　　　

 

 

　　　　

 

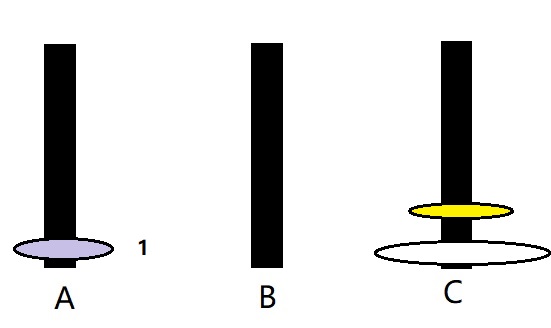
　　　　最后将 1号盘 移至 C柱

　　　　

 

 

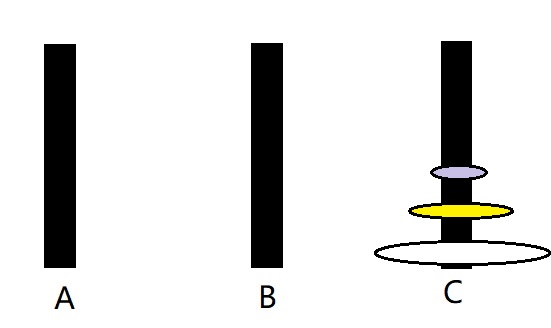
Hanoi塔 解题步骤：

1.将 A 上 n-1 个盘子移到B (借助C)

2.把 A 上 剩下的盘子移到C 

3.将 n-1 个盘子从B 移到 C (借助A)

 

 

！！！

不用死记A B C在各个盘移动时的站位,将他们想成

初始柱  过渡柱  目标柱  这样在敲代码时思路会清晰一些

 

代码实践：

#include<iostream>
using namespace std;

void move(char x1, char x2) {
    cout << x1 << "-->" << x2 << endl;
}


//A、B、C三个位置依次对应 初始柱/ 过渡柱/  目标柱【是对应的位置对应各种柱子（初始、过渡、目标柱） 不是ABC字母对应】
void hanoi(int n, char A, char B, char C) {        

    if (n == 1)
        move(A, C);
    else {
        hanoi(n - 1, A, C, B);        //A为初始柱  C为过渡柱  B为目标柱
        move(A, C);
        hanoi(n - 1, B, A, C);        //B为初始柱  A为过渡柱  C为目标柱
    }
}

int main() {
    cout << "输入盘子数： ";
    int p;
    cin >> p;
    char A = 'A', B = 'B', C = 'C';
    hanoi(p, A, B, C);
    return 0;
}

----------------------------------------------------小分割线----------------------------------------------

注意递归算法的两个必要条件递归出口和递归函数

认真分析如何将大问题分解为子问题　　　　

 这些需要多加练习~

==============================大分割线=========================

如有错误还是希望评论指正 ：）