机器学习技法 之 梯度提升决策树（Gradient Boosted Decision Tree）

梯度提升决策树从名字看是由三个部分组成，这里的提升（Boosted）指的是 AdaBoost 的运用，现在先看一下后两个部分提升决策树（Adaptive Boosted Decision Tree）。

提升决策树（Adaptive Boosted Decision Tree）

提升决策树顾名思义是将决策树作为 AdaBoost 的基模型。那么训练流程如下：

\[\begin{aligned} &\text { function AdaBoost-DTree( } \mathcal { D } \text { ) } \\ &\text { For } t = 1,2 , \ldots , T \\ &\qquad \text { reweight data by } \mathrm { u } ^ { ( t ) } \\ &\qquad \text { obtain tree } g _ { t } \text { by } \\ &\qquad \text { DTree } \left( \mathcal { D } , \mathbf { u } ^ { ( t ) } \right) \\ &\qquad \text { calculate 'vote' } \alpha _ { t } \text { of } g _ { t } \\ &\text { return } G = \text { Linearhypo } \left( \left\{ \left( g _ { t } , \alpha _ { t } \right) \right\} \right) \end{aligned} \]

显然现在需要一个决策树作为 加权基算法（Weighted Base Algorithm）。所以现在需要使用实现决策树 \(\text { DTree } \left( \mathcal { D } , \mathbf { u } ^ { ( t ) } \right)\) 可以接受加权特征。但是由于决策树有很多前人的巧思或者说很复杂，很难找出跟 \(E_\text{in}\) 有关的所有项，将权重加入。所以这时选择退回到复制样本数据而不是直接把权重直接交给决策树。即从重赋予权重（Re-weighting）退回到重采样（Re-sample）。

如何使用 bootstrap 实现权重信息的传递呢？这里进入采样概率的想法。

什么意思呢？那在 Original AdaBoost 中使用权重代替样本复制，那么现在为了使得决策树模型可以接受权重信息，需要根据权重对于样本进行同倍数的复制，这一过程体现在重新采样中便是使用采样概率，即所有样本被选择的概率不是一样的而是与自己的权重单调相关。也就是有概率的 bootstrap，生成所需的训练样本集 \(\tilde \mathcal{D}_t\)。

所以提升决策树（AdaBoost-DTree）经常通过 AdaBoost + sample \(\propto \mathbf { u } ^ { ( t ) } + \operatorname { DTree } \left( \tilde { \mathcal { D } } _ { t } \right)\) 实现。

弱决策树（Weak Decision Tree）

在前文决策树的学习中，可以知道只要数据无噪声，一颗完全长成树的 \(E_{\text{in}} = 0\) ，这不仅仅是过拟合的问题。在 AdaBoost 中时，如果采样的结果与权重矩阵效果完全一样，那么便可以训练处一颗完全长成树，也就是说\(E^{u}_{\text{in}} = 0\)，也就是错误率 \(\epsilon _ { t } = 0\)，最终导致 \(\alpha_t = \ln(\mathbf { \star } _ { t }) = \ln \sqrt { \frac { 1 - \epsilon _ { t } } { \epsilon _ { t } }} \rightarrow \inf \rightarrow\) autocracy（独裁者），所以应该让现在的算法弱一些。

具体的方法有：

1. 剪枝（pruned）: 使用原来剪枝策略或者只是限制树的高度
2. 不完全采样（some）: 数据少一些，决策树也“难为无米之炊”。

所以提升决策树（AdaBoost-DTree）另一实现形式是 AdaBoost + sample \(\propto \mathbf { u } ^ { ( t ) } + \text{pruned } \operatorname { DTree } \left( \tilde { \mathcal { D } } _ { t } \right)\) 。

极端状态则是决策树的高度（height）小于等于 1，也就是 C&RT 中就只剩下分钟条件（branching criteria）\(b(\mathbf{x})\)：

\[b ( \mathbf { x } ) = \underset { \text { decision stumps } h ( \mathbf { x } ) } { \operatorname { argmin } } \sum _ { c = 1 } ^ { 2 } | \mathcal { D } _ { c } \text { with } h | \cdot \text { impurity } \left( \mathcal { D } _ { c } \text { with } h \right) \]

可以看出这便是 AdaBoost-Stump，也就是说 AdaBoost-Stump 是 AdaBoost-DTree 的一种。当然这么简单的模型则不需要进行 sampling 的操作了。

AdaBoost 的优化视角

回顾 AdaBoost 中的权值更新过程：

\[\begin{aligned} u _ { n } ^ { ( t + 1 ) } & = \left\{ \begin{array} { l l } u _ { n } ^ { ( t ) } \cdot \mathbf { \star } _ { t } & \text { if incorrect } \\ u _ { n } ^ { ( t ) } / \mathbf { \star } _ { t } & \text { if correct }\end{array} \right. \\ & = u _ { n } ^ { ( t ) } \cdot \mathbf { \star } _ { t } ^{ - y _ { n } g _ { t } \left( \mathbf { x } _ { n } \right) }= u _ { n } ^ { ( t ) } \cdot \exp \left( - y _ { n } \alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) \right) \end{aligned} \]

也就是说

\[u _ { n } ^ { ( T + 1 ) } = u _ { n } ^ { ( 1 ) } \cdot \prod _ { t = 1 } ^ { T } \exp \left( - y _ { n } \alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) \right) = \frac { 1 } { N } \cdot \exp \left( - y _ { n } \sum _ { t = 1 } ^ { T } {\alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) }\right) \]

由于 \(G ( \mathbf { x } ) = \operatorname { sign } \left( \sum _ { t = 1 } ^ { T } \alpha _ { t } g _ { t } ( \mathbf { x } ) \right)\)，所以在这里将 \(\sum _ { t = 1 } ^ { T } \alpha _ { t } g _ { t } ( \mathbf { x } )\) 称为 \(\{g_t\}\) 在 \(\mathbf{x}\) 上的投票分数（voting score）。也就是说 \(u _ { n } ^ { ( T + 1 ) } \propto \exp \left( - y _ { n } \left( \text { voting score on } \mathbf { x } _ { n } \right) \right)\) ，即两者单调相关。

从另一个角度来看

\[G \left( \mathbf { x } _ { n } \right) = \operatorname { sign } \left( \overbrace { \sum _ { t = 1 } ^ { T } \underbrace { \alpha _ { t } } _ { \mathbf {w} _ { i } } \underbrace { g _ { t } \left( \mathbf { x } _ { n } \right) } _ { \phi _ { i } (\mathbf{x}_n)} }^{\text{voting score}} \right) \]

回顾一下在 hard-margin SVM 的间隔求取公式为：

\[\text { margin } = \frac { y _ { n } \cdot \left( \mathbf { w } ^ { T } \boldsymbol { \phi } \left( \mathbf { x } _ { n } \right) + b \right) } { \| \mathbf { w } \| } \]

是不是很类似呢，只是没有 \(b\) 而已。所以从这个角度来看：

\[y _ { n } ( \text { voting score } ) = \text { signed \& unnormalized margin } \]

也就是说：

\[\begin{aligned} & \quad u _ { n } ^ { ( T + 1 ) } \text{ small } \\ &\Rightarrow \frac { 1 } { N } \cdot \exp \left( - y _ { n } \sum _ { t = 1 } ^ { T } \underbrace{\alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) }_{G(\mathbf{x})}\right) \text{ small } \\ &\Rightarrow y _ { n } ( \text { voting score } )\text{ positive \& large } \end{aligned} \]

所以说如果 AdaBoost 学习过程会不断优化减小 \(u _ { n } ^ { ( T + 1 ) }\) ，那么也是一种 large-margin 算法。事实证明 AdaBoost 是会降低 \(\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) }\) 的，也就是说 AdaBoost 在最小化下面这式子：

\[\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( T + 1 ) } = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \exp \left( - y _ { n } \sum _ { t = 1 } ^ { T } \alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) \right) \]

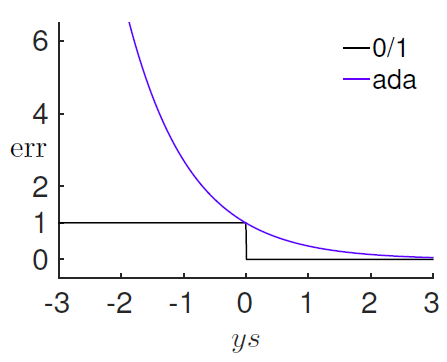
如果将投票分数 \(s = \sum _ { t = 1 } ^ { T } \alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right)\) 用于测量预测误差的话，可以写出 0/1 误差测量表达式：

\[\operatorname { err } _ { 0 / 1 } ( s , y ) = \left[ \kern-0.15em \left[ys \leq 0 \right] \kern-0.15em \right] \]

那现在提出另一种误差测量方式指数误差测量（exponential error
measure）：

\[\widehat { \operatorname { err } } _ { A D A } ( s , y ) = \exp ( - y s ) \]

绘制出两个误差测量函数曲线图：

可见 \(\widehat { \operatorname { err } } _ { A D A } ( s , y )\) 是一种 \(\operatorname { err } _ { 0 / 1 } ( s , y )\) 的凸上限误差测量函数。所以说不断降低 \(u _ { n } ^ { ( T + 1 ) }\) 也是一种降低 0/1 误差的过程，也就是说 \(\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \Leftrightarrow \hat { E } _ { \mathrm { ADA } }\)。

现在回忆一下梯度下降法的迭代公式：

\[\min _ { \| \mathbf { v } \| = 1 } E _ { \mathrm { in } } \left( \mathbf { w } _ { t } + \eta \mathbf { v } \right) \approx \underbrace { E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) } _ { \mathrm { known } } + \underbrace { \eta } _ { \text {given positive } } \mathbf { v } ^ { T } \underbrace { \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) } _ { \mathrm { known } } \]

实际上就是在当前的位置上，找到下一个比较好的位置，那么现在就需要当前位置，以及移动的方向和距离。类比于 AdaBoost 的话，便是 \(u _ { n } ^ { ( T ) } \Rightarrow u _ { n } ^ { ( T + 1 ) }\)过程，也就是

\[\begin{aligned} \min _ { h } \hat { E } _ { \mathrm { ADA } } & = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \exp \left( - y _ { n } \left( \sum _ { \tau = 1 } ^ { t - 1 } \alpha _ { \tau } g _ { \tau } \left( \mathbf { x } _ { n } \right) + \eta h \left( \mathbf { x } _ { n } \right) \right) \right) \\ & = \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \exp \left( - y _ { n } \eta h \left( \mathbf { x } _ { n } \right) \right) \\ & \mathop{\approx} \limits^{Taylor} \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \left( 1 - y _ { n } \eta h \left( \mathbf { x } _ { n } \right) \right) = \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } - \eta \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } y _ { n } h \left( \mathbf { x } _ { n } \right) \end{aligned} \]

所以说现在需要好的 \(h\) 用于最小化 \(- \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } y _ { n } h \left( \mathbf { x } _ { n } \right) = \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } (-y _ { n } h \left( \mathbf { x } _ { n } \right))\)。

那么在二分类中 \(y _ { n }\) 和 \(h \left( \mathbf { x } _ { n } \right))\) 均 \(\in \{-1,+1\}\)，那么有：

\[\begin{aligned} \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \left( - y _ { n } h \left( \mathbf { x } _ { n } \right) \right) & = \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \cdot \left\{ \begin{array} { c c } - 1 & \text { if } y _ { n } = h \left( \mathbf { x } _ { n } \right) \\ + 1 & \text { if } y _ { n } \neq h \left( \mathbf { x } _ { n } \right) \end{array} \right.\\ & = - \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } + \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \cdot \left\{ \begin{array} { c c } 0 & \text { if } y _ { n } = h \left( \mathbf { x } _ { n } \right) \\ 2 & \text { if } y _ { n } \neq h \left( \mathbf { x } _ { n } \right) \end{array} \right. \rightarrow \text{这实际上就是含权重样本的 }N \cdot E _ { \text {in } } \\ & = - \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } + 2 E _ { \text {in } } ^ { \mathbf { u } ^ { ( t ) } } ( h ) \cdot N \end{aligned} \]

同时在 AdaBoost 中，算法 \(\mathcal A\) 会最小化 \(E _ { \text {in } } ^ { \mathbf { u } ^ { ( t ) } } ( h )\)，也就是说为 \(\min _ { h } \hat { E } _ { \mathrm { ADA } }\) 找出了好的优化方向，这里指的是函数 \(h\)。

当通过算法 \(\mathcal A\) 找到最佳的函数（方向）\(g_t\) 后，优化目标转换为：

\[\min _ { \eta } \widehat { E } _ { \mathrm { ADA } } = \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \exp \left( - y _ { n } \eta g _ { t } \left( \mathbf { x } _ { n } \right) \right) \]

那么现在就可以通过不断的向正确的方向小步移动便可以得到最佳值，那有没有什么方法可以找到可以移动当前状态的最佳步长（optimal \(\eta_t\)，steepest descent for optimization，当然这是贪心的，因为只管当前移动步长的最佳值）而不用蹑手蹑脚呢？

现在分情况讨论一下，对于分类的正确与否：

\[\begin{array} { l } y _ { n } = g _ { t } \left( \mathbf { x } _ { n } \right) : u _ { n } ^ { ( t ) } \exp ( - \eta ) \\ y _ { n } \neq g _ { t } \left( \mathbf { x } _ { n } \right) : u _ { n } ^ { ( t ) } \exp ( + \eta ) \end{array} \]

那么再根据 AdaBoost 中的定义：

\[\epsilon _ { t } = \frac {\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \left[ \kern-0.15em \left[y _ { n } \neq g _ { t } \left( \mathbf { x } _ { n } \right) \right] \kern-0.15em \right] } { \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } } \]

那么 \(\widehat { E } _ { \mathrm { ADA } }\) 可以改写为：

\[\begin{aligned} \widehat { E } _ { \mathrm { ADA } } &= {\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t) } \left[ \kern-0.15em \left[y _ { n } \neq g _ { t } \left( \mathbf { x } _ { n } \right) \right] \kern-0.15em \right] } \exp ( + \eta ) + {\sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t) } \left[ \kern-0.15em \left[y _ { n } = g _ { t } \left( \mathbf { x } _ { n } \right) \right] \kern-0.15em \right] } \exp ( - \eta ) \\ & = \left( \sum _ { n = 1 } ^ { N } u _ { n } ^ { ( t ) } \right) \cdot \left( \left( 1 - \epsilon _ { t } \right) \exp ( - \eta ) + \epsilon _ { t } \exp ( + \eta ) \right) \end{aligned} \]

对于凸函数的最小化问题，其必要条件是导数为零：

\[\frac { \partial \widehat { E } _ { \mathrm { ADA } } } { \partial \eta } = 0 \]

可以解出：

\[\eta _ { t } = \ln \sqrt { \frac { 1 - \epsilon _ { t } } { \epsilon _ { t } } } = \alpha _ { t } \]

所以说 AdaBoost 通过对估计函数的梯度获得了最佳步长（最陡梯度）（steepest descent with approximate functional gradient），是一种最速梯度下降法（steepest gradient descent）。

梯度提升（Gradient Boosting）

前面已经证明，对于二分类问题（binary-output hypothesis \(h\)），AdaBoost 在不断地对 \(\eta\, \& \, h\) 做最佳化。

\[\min _ { \eta } \min _ { h } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \exp \left( - y _ { n } \left( \sum _ { \tau = 1 } ^ { t - 1 } \alpha _ { \tau } g _ { \tau } \left( \mathbf { x } _ { n } \right) + \eta h \left( \mathbf { x } _ { n } \right) \right) \right) \]

这样的话，便可以将指数误差拓展到任意误差测量函数（allows extension to different err for regression/soft classification/etc.），同时也不在拘泥于二分类问题，对于任意的假设函数 \(h\) 均适用，可以改写为：

\[\min _ { \eta } \min _ { h } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \operatorname { err } \left( \sum _ { \tau = 1 } ^ { t - 1 } \alpha _ { \tau } g _ { \tau } \left( \mathbf { x } _ { n } \right) + \eta h \left( \mathbf { x } _ { n } \right) , y _ { n } \right) \]

GradientBoost for Regression

用于回归模型的话，误差检测函数为平方误差（square error）：

\[\min _ { \eta } \min _ { h } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \operatorname { err } \left( \underbrace {\sum _ { \tau = 1 } ^ { t - 1 } \alpha _ { \tau } g _ { \tau } \left( \mathbf { x } _ { n } \right) } _ { s _ { n } } + \eta h \left( \mathbf { x } _ { n } \right) , y _ { n } \right) \text { with err } ( s , y ) = ( s - y ) ^ { 2 } \]

知识回顾：

泰勒展开

\[\begin{aligned} f ( x ) &= \sum _ { i = 0 } ^ { n } \frac { f ^ { ( i ) } \left( x _ { 0 } \right) } { i ! } \left( x - x _ { 0 } \right) ^ { i }\\ & = f \left( x _ { 0 } \right) + f ^ { \prime } \left( x _ { 0 } \right) \left( x - x _ { 0 } \right) + \frac { f ^ { ( 2 ) } \left( x _ { 0 } \right) } { 2 ! } \left( x - x _ { 0 } \right) ^ { 2 } + \cdots + \frac { f ^ { ( n ) } \left( x _ { 0 } \right) } { n ! } \left( x - x _ { 0 } \right) ^ { n } \end{aligned} \]

其中 \(s_n\) 和 \(y_n\) 为固定值，那么上式在 \(s = s_n\) 进行一阶泰勒展开可以改写为：

\[\begin{aligned} & \min _ { h } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \operatorname { err } \left( \underbrace {\sum _ { \tau = 1 } ^ { t - 1 } \alpha _ { \tau } g _ { \tau } \left( \mathbf { x } _ { n } \right) } _ { s _ { n } } + \eta h \left( \mathbf { x } _ { n } \right) , y _ { n } \right) \\ 在 s_n 处泰勒展开 \rightarrow \mathop{\approx} & \min _ { h } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \underbrace { \operatorname { err } \left( s _ { n } , y _ { n } \right) } _ { \text {constant } } + \left. \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \eta h \left( \mathbf { x } _ { n } \right) \frac { \partial \operatorname { err } \left( s , y _ { n } \right) } { \partial s } \right| _ { S = S _ { n } } \\ = & \min _ { h } \text { constants } + \frac { \eta } { N } \sum _ { n = 1 } ^ { N } h \left( \mathbf { x } _ { n } \right) \cdot 2 \left( s _ { n } - y _ { n } \right) \end{aligned} \]

那么为了保证后半部分最小，那么每个部分应该满足：

\[h \left( \mathbf { x } _ { n } \right) = - k \left( s _ { n } - y _ { n } \right) \]

也就是说每一项均为负数，同时 \(k\) 越大，后半部分越小。但是由于步长由 \(\eta\) 决定，所以 \(k\) 没必要这么大。同时在梯度下降法中这只代表了方向，所以原始的梯度下降法中需要使得 \(\| h(\mathbf { x }) \| = 1\)，但是这里不想加入约束条件，所以在后半部分加入 \(h \left( \mathbf { x } _ { n } \right)^2\) 用于限制 \(h \left( \mathbf { x } _ { n } \right)\) 的大小（类似于正则化）。

\[\begin{aligned} \min _ { h } \quad& \text { constants } + \frac { \eta } { N } \sum _ { n = 1 } ^ { N } \left( 2 h \left( \mathbf { x } _ { n } \right) \left( s _ { n } - y _ { n } \right) + \left( h \left( \mathbf { x } _ { n } \right) \right) ^ { 2 } \right) \\ & = \text { constants } + \frac { \eta } { N } \sum _ { n = 1 } ^ { N } \left( -\left( s _ { n } - y _ { n } \right) ^ 2+ \left( h \left( \mathbf { x } _ { n } \right) - \left( y _ { n } - s _ { n } \right) \right) ^ { 2 } \right) \\ & = \text { constants } + \frac { \eta } { N } \sum _ { n = 1 } ^ { N } \left( \text { constant } + \left( h \left( \mathbf { x } _ { n } \right) - \left( y _ { n } - s _ { n } \right) \right) ^ { 2 } \right) \end{aligned} \]

那么现在只需要使得：

\[h \left( \mathbf { x } _ { n } \right) - \left( y _ { n } - s _ { n } \right) = 0 \]

所以只需要解一个关于\(\left\{ ( \mathbf { x } _ { n } , \underbrace { y _ { n } - s _ { n } } _ { \text {residual } } ) \right\}\) 的平方误差回归问题（squared-error regression）即可。所以在GradientBoost for Regression中是使用回归方法找出一个 \(g_t = h\)。

在获取到 \(g_t\) 之后，原优化问题可以写为：

\[\min _ { \eta } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( s _ { n } + \eta g _ { t } \left( \mathbf { x } _ { n } \right) - y _ { n } \right) ^ { 2 } = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \left( y _ { n } - s _ { n } \right) - \eta g _ { t } \left( \mathbf { x } _ { n } \right) \right) ^ { 2 } \]

所以通过一个关于 \(\left\{ \left( g _ { t } - \text { transformed input, residual } \right) \right\}\) 的单变量的线性回归便可以得出 \(\eta\) 也就是 \(\alpha_t\) 的最优解。即 \(\alpha_t\) = optimal \(\eta\) by \(g_t\) -transformed linear regression

有了前文的求解过程，那么Gradient Boosted Decision Tree (GBDT) 的具体实现步骤写为：

\[\begin{array} { l } s _ { 1 } = s _ { 2 } = \ldots = s _ { N } = 0 \\ \text { for } t = 1,2 , \ldots , T \\ \qquad \text { 1. obtain } g _ { t } \text { by } \mathcal { A } \left( \left\{ \left( \mathbf { x } _ { n } , y _ { n } - s _ { n } \right) \right\} \right) \text { where } \mathcal { A } \text { is a (squared-error) } \\ \text { regression algorithm } \rightarrow \text{ Decision Tree} \\ \qquad \text { 2. compute } \alpha _ { t } = \text { OneVar Linear Regression } \left( \left\{ \left( g _ { t } \left( \mathbf { x } _ { n } \right) , y _ { n } - s _ { n } \right) \right\} \right) \\ \qquad \text { 3. update } s _ { n } \leftarrow s _ { n } + \alpha _ { t } g _ { t } \left( \mathbf { x } _ { n } \right) \\ \text { return } G ( \mathbf { x } ) = \sum _ { t = 1 } ^ { T } \alpha _ { t } g _ { t } ( \mathbf { x } ) \end{array} \]

其中 \(s _ { 1 } = s _ { 2 } = \ldots = s _ { N } = 0\) 代表了一开始在原始的 Regression 问题上求取，之后再在余数上进行求取。这里 Gradient Boosting 介绍了 Regression 的实现，其中如果使用决策树做回归分析的话，那便的出了GBDT（Gradient Boosted Decision Tree），当然 Classification/Soft Classification 的实现也差不多，最终可以实现 Putting Everything Together。