OI集训 Day6

Content：Data Structures;
Date：2025.7.22

概览

可持久化线段树
虚树

具体内容

可持久化线段树

可持久化线段树实现可持久化数组

我们对每一个版本维护一颗线段树，这样显然空间复杂度是 \(\Theta(nm)\) 的，肯定不对。

接下来我们通过观察可以发现，其实新版本线段树上的很多节点与原线段树
上的节点是重复的，极大地浪费了空间。

我们考虑对那些不用修改的节点进行空间上的优化，具体如下：

假设线段树节点 \(k\) 维护的区间为 \([l,r]\)，其中点为 \(mid\)。
我们对新版本新建了一个节点 \(k'\)，接下来分两种情况讨论：
- 如果区间 \([l, mid]\) 包括我们要修改的位置，则 \(lc(k') = cnt + 1\)，\(rc(k') = rc(k)\)。即我们继承不用修改的节点。
- 对于区间 \([mid + 1, r]\) 同理。

这样我们就极大地降低了空间复杂度。

放张 OI Wiki 的图在这里方便理解：

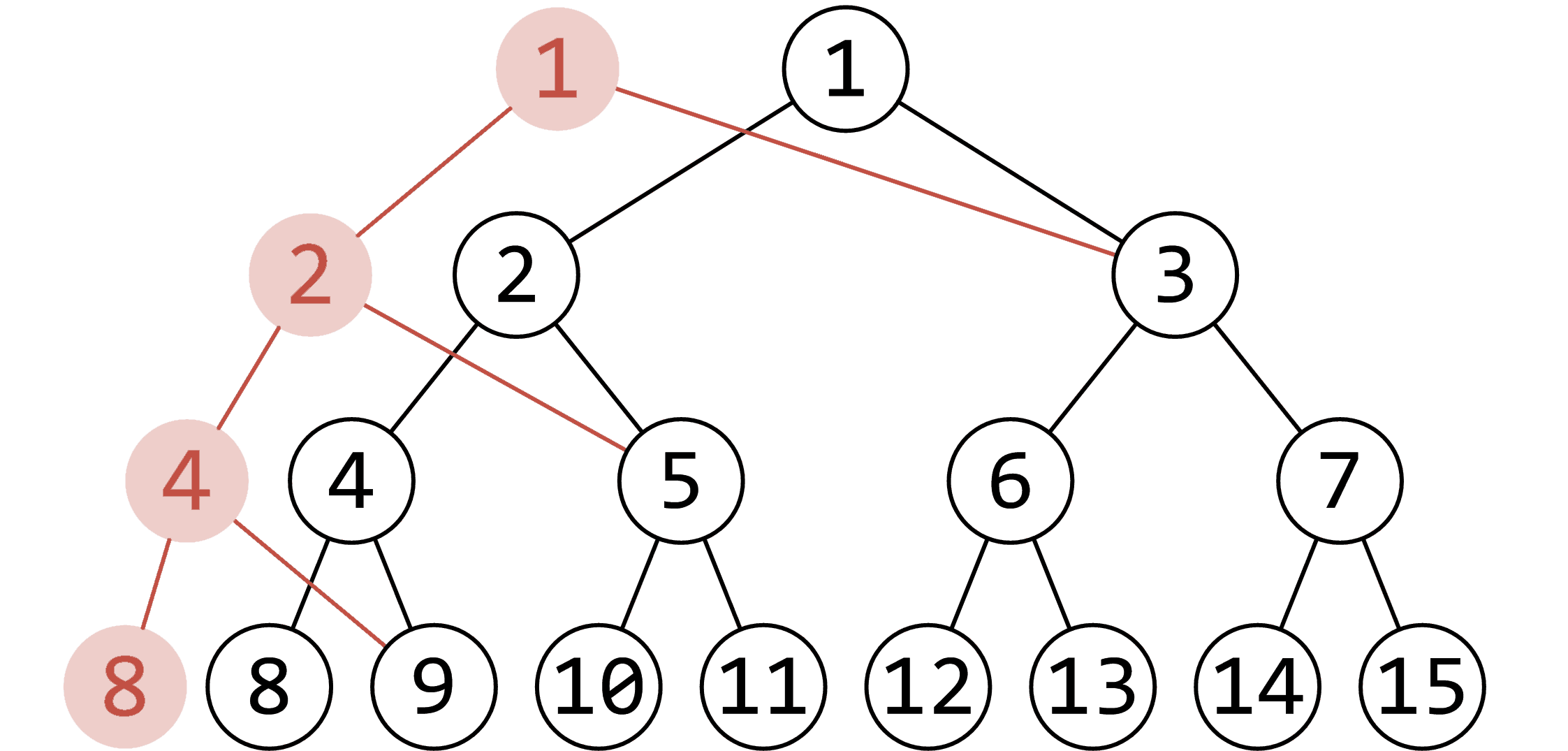
可持久化线段树

例题：洛谷 P3919 可持久化线段树1

我们直接按题意维护即可。

Code

#include <bits/stdc++.h> 

using std::cin;
using std::cout; 

constexpr int N = 1e6 + 5;
int n, m, version, op, p, c;
int array[N]; 

class SegmentTree {
public:
    class Node {
    public:
        int left, right;
        int left_child, right_child;
        long long value; 

        explicit Node(const int l = 0, const int r = 0, const int lc = 0, const int rc = 0, nst int val = 0) :
            left(l), right(r), left_child(lc), right_child(rc), value(val) {}
    }; 

    int count_node = 0, root[N] = {};
    Node node_info[N * 30]; 

    void copy(int& root) {
        const int new_root = ++count_node;
        node_info[new_root] = node_info[root];
        root = new_root;
    } 

    void build_tree(int& k, const int left, const int right) {
        k = ++count_node;
        node_info[k] = Node(left, right); 

        if (node_info[k].left == node_info[k].right) {
            node_info[k].value = array[left];
            return void();
        } 

        const int mid = (node_info[k].left + node_info[k].right) >> 1;
        build_tree(node_info[k].left_child, left, mid);
        build_tree(node_info[k].right_child, mid + 1, right);
    } 

    void insert_node(int& k, const int position, const int value) {
        copy(k); 

        if (node_info[k].left == node_info[k].right) {
            node_info[k].value = value;
            return void();
        } 

        const int mid = (node_info[k].left + node_info[k].right) >> 1; 

        if (position <= mid)
            insert_node(node_info[k].left_child, position, value);
        else
            insert_node(node_info[k].right_child, position, value);
    } 

    long long query(int& k, const int position) {
        if (node_info[k].left == node_info[k].right) return node_info[k].value; 

        const int mid = (node_info[k].left + node_info[k].right) >> 1; 

        if (position <= mid) return query(node_info[k].left_child, position);
        return query(node_info[k].right_child, position);
    }
} tr; 

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 

    cin >> n >> m; 

    for (int i = 1; i <= n; i++) cin >> array[i]; 

    tr.root[0] = 1;
    tr.build_tree(tr.root[0], 1, n); 

    for (int i = 1; i <= m; i++) {
        cin >> version >> op >> p; 

        if (op == 1) {
            cin >> c; 

            tr.root[i] = tr.root[version];
            tr.insert_node(tr.root[i], p, c);
        } else {
            cout << tr.query(tr.root[version], p) << '\n';
            tr.root[i] = tr.root[version];
        }
    } 

    return 0;
}

例题2：洛谷 P3834 可持久化线段树2

我们用权值线段树维护每一个数字出现的次数，对于每一个下标维护新的版本，所以在区间 \([l,r]\) 中的权值区间 \([wl, wr]\) 出现的次数为 \(sum_{wl, wr, r} - sum_{wl, wr, r - 1}\)。

然后在线段树上二分找第 \(k\) 小即可。

Code

#include <bits/stdc++.h> 

using std::vector; 

constexpr int kMaxN = 2e5 + 5;
int n, m, left, right, k, array[kMaxN];
vector <int> current; 

class SegmentTree {
public:
    class Node {
    public:
        int left_child, right_child;
        int count; 

        explicit Node(const int lc = 0, const int rc = 0, const int c = 0) :
            left_child(lc), right_child(rc), count(c) {}
    }; 

    int count_node = 0, root[kMaxN] = {};
    Node tr[kMaxN * 20]; 

    void copy_node(int& root) {
        const int new_root = ++count_node;
        tr[new_root] = tr[root];
        root = new_root;
    } 

    void build_tree(int& root, const int left, const int right) {
        copy_node(root); 

        if (left == right) return void(); 

        const int mid = (left + right) >> 1;
        build_tree(tr[root].left_child, left, mid);
        build_tree(tr[root].right_child, mid + 1, right);
    } 

    void update_node(int& root, const int left, const int right, const int position) {
        copy_node(root);
        tr[root].count++; 

        if (left == right) return void(); 

        const int mid = (left + right) >> 1;
        if (position <= mid)
            update_node(tr[root].left_child, left, mid, position);
        else
            update_node(tr[root].right_child, mid + 1, right, position);
    } 

    int query_kth(const int root_l, const int root_r, const int left, const int right, const int k) {
        if (left == right) return left; 

        const int mid = (left + right) >> 1;
        const int lc1 = tr[root_l].left_child;
        const int lc2 = tr[root_r].left_child;
        const int pre_sum = tr[lc2].count - tr[lc1].count; 

        if (k <= pre_sum) return query_kth(tr[root_l].left_child, tr[root_r].left_child, left, mid, k);
        return query_kth(tr[root_l].right_child, tr[root_r].right_child, mid + 1, right, k - pre_sum);
    }
} tr; 

int get_index(int value) {
    using std::lower_bound;
    return lower_bound(current.begin(), current.end(), value) - current.begin() + 1;
} 

int main() {
    using std::cin;
    using std::cout;
    using std::sort;
    using std::unique; 

    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 

    cin >> n >> m; 

    for (int i = 1; i <= n; i++) {
        cin >> array[i];
        current.push_back(array[i]);
    } 

    sort(current.begin(), current.end());
    current.erase(unique(current.begin(), current.end()), current.end());
    tr.build_tree(tr.root[0], 1, current.size()); 

    for (int i = 1; i <= n; i++) {
        // ! 注意不要把 tr.root[i - 1] 填入引用中，不然在修改时 tr.root[i - 1] 的值会改变。
        tr.root[i] = tr.root[i - 1];
        tr.update_node(tr.root[i], 1, current.size(), get_index(array[i]));
    } 

    for (int i = 1; i <= m; i++) {
        cin >> left >> right >> k;
        cout << current[tr.query_kth(tr.root[left - 1], tr.root[right], 1, current.size(), k) - 1] << '\n';
    } 

    return 0;
}

例题3：洛谷 P2633 Count on a Tree.

我们用类似树上差分的思路维护即可。

Code

#include <bits/stdc++.h> 

constexpr int kMaxN = 1e5 + 5;
int head[kMaxN], cnt = 0;
int n, m, u, v, k, last;
int initial_weight[kMaxN];
int siz[kMaxN], son[kMaxN], dep[kMaxN], fa[kMaxN], top[kMaxN];
std::vector<int> tmp; 

class Edge {
public:
    int to, next; 

    explicit Edge(const int t = 0, const int ne = 0) : to(t), next(ne) {}
} e[kMaxN << 2]; 

class PresidentTree {
public:
    class Node {
    public:
        int left_child, right_child;
        int count; 

        explicit Node(const int lc = 0, const int rc = 0, const int c = 0) : left_child(lc), right_child(rc), count(c) {}
    }; 

    int count_node = 0, root[kMaxN] = {};
    Node tr[kMaxN * 20]; 

    void copy(int& root) {
        const int new_root = ++count_node;
        tr[new_root] = tr[root];
        root = new_root;
    } 

    void insert(int& root, const int left, const int right, const int pos) {
        copy(root);
        tr[root].count++; 

        if (left == right) return void(); 

        const int mid = (left + right) >> 1;
        if (pos <= mid)
            insert(tr[root].left_child, left, mid, pos);
        else
            insert(tr[root].right_child, mid + 1, right, pos);
    } 

    int query_kth(int& u, int& v, int left, int right, int x, int y, int kth) {
        if (left == right) return left; 

        const int mid = (left + right) >> 1;
        const int sum = tr[tr[u].left_child].count + tr[tr[v].left_child].count - tr[tr[x].left_child].count - tr[tr[y].left_child].count; 

        if (kth <= sum) return query_kth(tr[u].left_child, tr[v].left_child, left, mid, tr[x].left_child, tr[y].left_child, kth);
        return query_kth(tr[u].right_child, tr[v].right_child, mid + 1, right, tr[x].right_child, tr[y].right_child, kth - sum);
    }
} tr; 

void add_edge(const int u, const int v) {
    e[cnt] = Edge(v, head[u]);
    head[u] = cnt++;
} 

int get_index(const int value) {
    using std::lower_bound;
    return lower_bound(tmp.begin(), tmp.end(), value) - tmp.begin() + 1;
} 

void dfs(const int u, const int father) {
    fa[u] = father;
    dep[u] = dep[father] + 1;
    siz[u] = 1; 

    tr.root[u] = tr.root[father];
    tr.insert(tr.root[u], 1, n, get_index(initial_weight[u])); 

    for (int i = head[u]; ~i; i = e[i].next) {
        const int v = e[i].to;
        if (v == father) continue; 

        dfs(v, u);
        siz[u] += siz[u]; 

        if (son[u] == 0 || siz[v] > siz[son[u]]) son[u] = v;
    }
} 

void dfs2(const int u, const int topx) {
    top[u] = topx; 

    if (son[u] == 0) return void(); 

    dfs2(son[u], topx); 

    for (int i = head[u]; ~i; i = e[i].next) {
        const int v = e[i].to;
        if (v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
} 

int get_LCA(int u, int v) {
    using std::swap; 

    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        u = fa[top[u]];
    } 

    if (dep[u] > dep[v]) swap(u, v);
    return u;
} 

int main() {
    using std::cin;
    using std::cout;
    using std::sort;
    using std::unique; 

    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 

    std::memset(head, -1, sizeof(head)); 

    cin >> n >> m; 

    for (int i = 1; i <= n; i++) {
        cin >> initial_weight[i];
        tmp.push_back(initial_weight[i]);
    } 

    for (int i = 1; i < n; i++) {
        cin >> u >> v;
        add_edge(u, v);
        add_edge(v, u);
    } 

    sort(tmp.begin(), tmp.end());
    tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end()); 

    dfs(1, 0);
    dfs2(1, 1); 

    for (int i = 1; i <= m; i++) {
        cin >> u >> v >> k; 

        u ^= last;
        int LCA = get_LCA(u, v);
        last = tmp[tr.query_kth(tr.root[u], tr.root[v], 1, n, tr.root[LCA], tr.root[fa[LCA]], k) - 1]; 

        cout << last << '\n';
    } 

    return 0;
}

可持久化区间线段树

我们将标记一起放入节点信息中并一起维护即可，和普通线段树一样。就不放代码了。

可持久化区间线段树

我们将标记一起放入节点信息中并一起维护即可，和普通线段树一样。就不放代码了。

可持久化字典树

[!Bug] Unsubmitted
TODO 洛谷 P4735
Submission WA 64pts

虚树 (没听懂啊)

定义

给定节点集合 \(S\)，\(\forall u,v \in S\)，定义关键节点为 \(u, v, \operatorname{LCA}(u, v)\)。

然后对关键节点在原树上的祖先关系建树，就得到了虚树。

应用

可以在树形 \(DP\) 中排除无关的节点，大大降低复杂度。

posted @ 2025-07-22 21:01 Fallen_Leaf 阅读(4) 评论(0) 收藏举报

刷新页面返回顶部

FallenLeaf

一个蒟蒻 OIer 的 blog

OI集训 Day6

概览

具体内容

可持久化线段树

可持久化线段树实现可持久化数组

可持久化区间线段树

可持久化区间线段树

可持久化字典树

虚树 (没听懂啊)

定义

应用

公告