OI集训 Day4
Content:Math
Date:2025.7.20
内容
- 矩阵
- 线性方程组
- 行列式
- 矩阵树定理
- 线性基
具体内容
矩阵
矩阵定义
将一些元素排列成若干行,每行放上相同数量的元素,就是一个矩阵 (Matrix)。
对于矩阵 \(A\) 的第 \(i\) 行,第 \(j\) 列,我们记作 \(a_{i,j}\) 或 \(a_{ij}\)。
对于举证 \(A_{m \times n}\),如果 \(m = n\),则我们称矩阵 \(A\) 为方阵。
矩阵基本操作
-
矩阵加法:对于矩阵 \(A_{m \times n}\), \(B_{m \times n}\), 我们定义矩阵加法为:
\[C_{i,j} = A_{i, j} + B_{i, j} \]即矩阵对应位置上的元素之和。
!> 注意
只有当两个矩阵的大小相同时,才可以进行矩阵加法。 -
标量乘法:对于矩阵 \(A_{m \times n}\) 和标量 \(x\), 我们定义矩阵的标量乘法为:
\[C_{i, j} = A_{i, j} \times x \] -
转置:对于矩阵 \(A_{m \times n}\),其转置为:
\[A^{T} = \begin{bmatrix} A_{j, i} \end{bmatrix} \] -
矩阵的拼接:对于矩阵 \(A_{m \times n_1}\),\(B_{m \times n_2}\),其拼接为记为 \((A \ | \ B)\),其大小为 \(m \times (n_1 + n_2)\)。
-
矩阵的乘法:对于矩阵 \(A_{m \times n}\) 和矩阵 \(B_{n \times k}\),其矩阵乘法定义为:
\[C_{i, j} = \sum_{x = 1}^{n} A_{i, x} \times B_{x, j} \]其中 \(i \in [1,n]\),\(j \in [1,k]\)。
对于矩阵乘法,有如下性质:- 矩阵乘法具备分配律:\((A + B)C = AC + BC\);
- 矩阵乘法具有结合律:\((AB)C = A(BC)\);
!> 注意
矩阵乘法不具备交换律! -
矩阵乘法单位元:
?> 矩阵乘法单位元
矩阵的乘法单位元 \(I\) 为矩阵主对角线上全部为 \(1\),其余均为 \(0\) 的 \(0/1\) 矩阵。 -
矩阵的逆:如果对于矩阵 \(A\) 存在矩阵 \(B\),使得 \(AB = I\),则 \(B\) 称作矩阵 \(A\) 的逆元,记作 \(A^{-1}\)。
对于逆元我们可以使用高斯消元求解。我们对矩阵 \((A \ | \ I)\) 进行高斯消元,最后会得到 \((I \ | \ B)\) (若无法把左边化为乘法单位元,则矩阵 \(A\) 不存在逆元),则 \(B\) 就为 \(A\) 的逆元。
矩阵与线性方程组
对于线性方程组
将未知数的系数写成矩阵的形式,用系数所在的矩阵的行表示未知数,我们就得到了线性方程组的矩阵 (增广矩阵) 表达形式:
对于线性方程组,我们通常会使用消元来求解。在矩阵表示下的线性方程组可以用高斯消元来求解。
高斯消元是通过对矩阵进行初等变换,以保证在方程的解不变的情况下求出方程的解。一般来说步骤如下 (记增广矩阵为 \(M\)):
- 枚举变量 \(i\) (\(i \in [1,m]\)) 表示当前要对未知元 \(x_i\) 进行消元操作。
- 寻找最大的 \(j \in [i,m]\),使得 \(a_{j, i} \ne 0\),交换 \(M_i \longleftrightarrow M_j\)。
- 将交换后的矩阵的第 \(i\) 行的未知元 \(x_i\) 的系数化为 \(1\),即: \(a_{i,j} \leftarrow \frac{a_{i,j}}{a_{i,i}}\) (\(j \in [1,m]\))。
- 用矩阵的第 \(i\) 行对矩阵的第 \(j\) (\(j \in [i + 1,m]\)) 行进行消元操作,即:\(a_{j,k} \leftarrow a_{j,k} - a_{j,k} \times a_{j,i}\)。
- 重复上述操作直到 \(i > n\) 或者找不到满足条件 \(2\) 中的 \(j\)。
最后的结果可能会有以下三种
- 如果 \(i < n\),且存在 \(j\) 使得 \(a_{j,n} > 0\),则原线性方程组无解。
- 如果 \(i < n\),且对于 \(\forall j\) 满足 \(a_{j,n} = 0\),则原线性方程组有无数解。
- 否则原线性方程组有唯一解。
Code
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 105;
constexpr double eps = 1e-8;
class Matrix {
double mat[N][N] = {{0}};
int size = 0;
public:
Matrix() = default;
void input_matrix() {
cin >> size;
for (int i = 0; i < size; i++)
for (int j = 0; j <= size; j++)
cin >> mat[i][j];
}
int guess() {
int i, j, r = 0;
for (int c = 0; c < size; c++) {
int t = r;
for (i = t + 1; i < size; i++) {
if (abs(mat[i][c]) > abs(mat[t][c])) {
t = i;
}
}
if (abs(mat[t][c]) < eps) continue;
for (i = c; i <= size; i++) {
swap(mat[t][i], mat[r][i]);
}
for (i = size; i >= c; i--) {
mat[r][i] /= mat[r][c];
}
for (i = r + 1; i < size; i++) {
if (abs(mat[i][c]) > eps) {
for (j = size; j >= c; j--) {
mat[i][j] -= mat[r][j] * mat[i][c];
}
}
}
r++;
}
if (r < size) {
return -1;
}
for (i = size - 1; i >= 0; i--) {
for (j = i + 1; j < size; j++) {
mat[i][size] -= mat[i][j] * mat[j][size];
}
}
return 1;
}
int get_size() const { return size; }
double get_solution(int i) const { return mat[i][size]; }
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
Matrix matrix;
matrix.input_matrix();
if (matrix.guess() == -1) {
cout << "No Solution\n";
} else {
for (int i = 0; i < matrix.get_size(); i++) {
double answer = matrix.get_solution(i);
if (abs(answer) < eps) {
answer = 0;
} else {
answer = round(answer * 100.00) / 100.00;
}
cout << setiosflags(ios::fixed) << setprecision(2) << answer << "\n";
}
}
return 0;
}
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
const double eps = 1e-8;
int n;
double a[N][N];
int gauss() {
int i, j, c, r = 0;
for (c = 0; c < n; c ++) {
int t = r;
for (i = t + 1; i < n; i ++)
if (abs(a[i][c]) > abs(a[t][c])) t = i;
if (abs(a[t][c]) < eps) continue;
for (i = c; i <= n; i ++) swap(a[t][i], a[r][i]);
for (i = n; i >= c; i --) a[r][i] /= a[r][c];
for (i = r + 1; i < n; i ++)
if (abs(a[i][c]) > eps)
for (j = n; j >= c; j --)
a[i][j] -= a[r][j] * a[i][c];
r ++;
}
if (r < n) {
for (i = r; i < n; i ++)
if (abs(a[i][n]) > eps) return 2;
return 1;
}
for (i = n - 1; i >= 0; i --)
for (j = i + 1; j < n; j ++)
a[i][n] -= a[i][j] * a[j][n];
return 0;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++) {
for (int j = 0; j <= n; j ++) {
scanf("%lf", &a[i][j]);
}
}
int t = gauss();
if (t == 2) puts("-1");
else if (t == 1) puts("0");
else {
for (int i = 0; i < n; i ++) {
printf("x%d=", i + 1);
if (abs(a[i][n]) < eps) a[i][n] = 0;
printf("%.2lf\n", a[i][n]);
}
}
return 0;
}
除了高斯消元外,我们还有另外一种消元的方式——高斯-约旦消元,下面给出代码。
洛谷 P3389
Code
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 105;
constexpr double eps = 1e-8;
class Matrix {
double mat[N][N] = {{0}};
int size = 0;
public:
Matrix() = default;
void input_matrix() {
cin >> size;
for (int i = 0; i < size; i++)
for (int j = 0; j <= size; j++)
cin >> mat[i][j];
}
int guess() {
int i, j, r = 0;
for (int c = 0; c < size; c++) {
int t = r;
for (i = t + 1; i < size; i++) {
if (abs(mat[i][c]) > abs(mat[t][c])) {
t = i;
}
}
if (abs(mat[t][c]) < eps) continue;
for (i = c; i <= size; i++) {
swap(mat[t][i], mat[r][i]);
}
for (i = size; i >= c; i--) {
mat[r][i] /= mat[r][c];
}
for (i = r + 1; i < size; i++) {
if (abs(mat[i][c]) > eps) {
for (j = size; j >= c; j--) {
mat[i][j] -= mat[r][j] * mat[i][c];
}
}
}
r++;
}
if (r < size) {
return -1;
}
for (i = size - 1; i >= 0; i--) {****
for (j = i + 1; j < size; j++) {
mat[i][size] -= mat[i][j] * mat[j][size];
}
}
return 1;
}
int get_size() const { return size; }
double get_solution(int i) const { return mat[i][size]; }
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
Matrix matrix;
matrix.input_matrix();
if (matrix.guess() == -1) {
cout << "No Solution\n";
} else {
for (int i = 0; i < matrix.get_size(); i++) {
double answer = matrix.get_solution(i);
if (abs(answer) < eps) {
answer = 0;
} else {
answer = round(answer * 100.00) / 100.00;
}
cout << setiosflags(ios::fixed) << setprecision(2) << answer << "\n";
}
}
return 0;
}
行列式
定义
对于矩阵 (通常为方阵) \(A_{n \times n}\),我们定义其行列式为:
其中 \(P_n\) 表示长度为 \(n\) 的所有排列的集合,\(\operatorname{sgn}(p)\) 表示 \((-1)^{排列 p 中的逆序对的个数}\)。
这里有一张快速求解行列式的图:
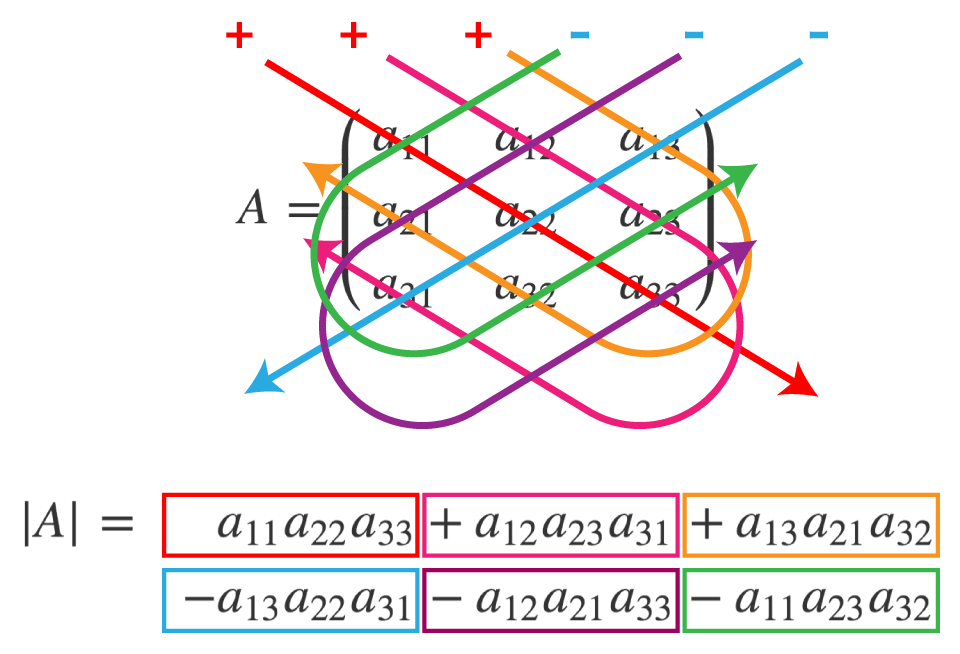
性质
-
对矩阵做行 (列) 交换,行列式反号。
?> 证明
根据排列的奇偶性,我们可以知道交换一个排列中的一对元素,其排列奇偶性也会发生变化,所以 \(\operatorname{sgn}(p) = -\operatorname{sgn}(p^{\prime})\),证毕。 -
对矩阵做行 (列) 数乘,行列式乘上同样的常数
?> 证明
我们知道一个排列包含 \([1,n]\) 之间的所有整数,所以被修改的元素会在每个连乘中出现且每个连乘中仅出现一次,所以可以提到整个式子的前面,证毕. -
对矩阵做行 (列) 加法,行列式不变。
求解行列式
Code
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 605;
int n;
long long p;
class Matrix {
long long mat[N][N] = {{}};
int size = 0;
public:
Matrix() = default;
void get_input(int n) {
size = n;
for (int i = 1; i <= size; i++) {
for (int j = 1; j <= size; j++) {
cin >> mat[i][j];
}
}
}
long long det(const long long ModValue) {
long long retval = 1, sgn = 1;
for (int i = 1; i <= size; i++) {
for (int j = i + 1; j <= size; j++) {
while (mat[i][i]) {
long long divide = mat[j][i] / mat[i][i];
for (int k = 1; k <= size; k++) {
mat[j][k] = (mat[j][k] - divide * mat[i][k] % ModValue + ModValue) % ModValue;
}
sgn = -sgn;
swap(mat[i], mat[j]);
}
sgn = -sgn;
swap(mat[i], mat[j]);
}
}
retval = sgn;
for (int i = 1; i <= size; i ++) {
retval = retval * mat[i][i] % ModValue;
}
return (retval + ModValue) % ModValue;
}
} matrix;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> p;
matrix.get_input(n);
cout << matrix.det(p) << '\n';
return 0;
}
矩阵树定理 (根本听不懂啊)
矩阵树定理是把图的生成树个数和矩阵行列式联系起来的一个定理。
?> 矩阵树定理
对于无自环 (允许重边) 的有向图 \(G = (V, E)\)。设出度矩阵 \(D(G)\),其中 \(\forall u \in V\),\(D_{u,u}\)表示点 \(u\) 的出度,其余位置全部为 \(0\)。而 \(A(G)\) 表示图 \(G\) 的邻接矩阵,其中 \(a_{i,j}\) 表示 \(i \to j\) 的边的数量 (\(i,j \in V\))。那么可以得到对应的拉普拉斯矩阵 \(L(G) = D(G) - A(G)\)。
\(L(G)\) 关于 \(L(G)_{k,k}\) 的余子式是以 \(k\) 为根节点的内向生成树的个数。
?> 余子式
对于矩阵 \(A\),\(A_{i,j}\) 的余子式定义为 \(A\) 去掉第 \(i\) 行第 \(j\) 列的矩阵行列式。
线性基
定义
在 \(K\) 维异或空间下,一个向量可以用一个 \([0,2^k)\) 内的整数表示 (即该数在二进制意义下的每一位都表示一个向量)。
对于一组向量 \(S = \{v_1, v_2, v_3, \dots, v_n\}\):
- \(S\) 中数字的异或和称为这些向量的线性组合。
- 若不存在非空子集 \(W \subset S\) 满足 \(\bigotimes_{v \in W} v = 0\),则称 \(S\) 线性无关。
- \(S\) 的所有子集的异或和的集合构成 \(S\) 的张成,记作 \(\operatorname{Span}(S)\)。
- \(S\) 的线性基是一个线性无关的向量集合 \(W\),满足 \(\operatorname{Span}(W) = \operatorname{Span}(S)\)。
- \(K\) 维空间的线性基 \(W\) 满足 \(\left\vert W \right\vert = K\)。
本文来自博客园,作者:Fallen_Leaf,转载请注明原文链接:https://www.cnblogs.com/FallenLeaf/p/18994736


 浙公网安备 33010602011771号
浙公网安备 33010602011771号