[bzoj2005][Noi2010]能量采集

来自FallDream的博客，未经允许，请勿转载，谢谢。

---

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。 栋栋的植物种得非常整齐，一共有n列，每列

有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。 由于能量汇集机器较大，不便移动，栋栋将它放在了

一个角上，坐标正好是(0, 0)。 能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能量的损失为2k + 1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于

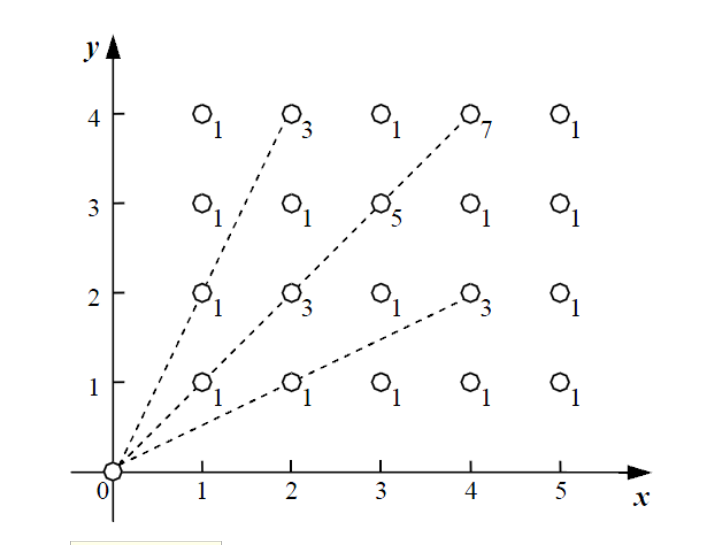
连接线段上存在一棵植物(1, 2)，会产生3的能量损失。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。 下面给出了一个能量采集的例子，其中n = 5，m = 4，一共有20

棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。 在这个例子中，总共产生了36的能量损失。

n,m<=100000

题解：假设n<m 不满足就交换呗，然后：

我们先枚举一个点被选的次数p，那么答案就是$$\sum_{p=1}^{n}p*\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{p}\rfloor}[gcd(i,j)=1]$$

把gcd用莫比乌斯函数代替$$\sum_{p=1}^{n}p*\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{p}\rfloor}\sum_{d|i,d|j}\mu(d)$$

然后从d看待这个式子$$\sum_{p=1}^{n}p*\sum_{d=1}^{\lfloor\frac{n}{p}\rfloor}\lfloor\frac{n}{pd}\rfloor\lfloor\frac{m}{pd}\rfloor$$

 枚举p，然后后面的式子只有根号种取值，复杂度$O(n\sqrt(n))$

#include<iostream>
#include<cstdio>
#define ll long long
#define MN 100000
using namespace std;
inline int read()
{
    int x = 0 , f = 1; char ch = getchar();
    while(ch < '0' || ch > '9'){ if(ch == '-') f = -1;  ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}
    return x * f;
}

bool b[MN+5];
int n,m,f[MN+5],s[MN/2],num=0;
ll ans;

ll calc(int x)
{
    int a=n/x,b=m/x;ll sum=0;
    for(int i=1,last;i<=a;i=last+1)
    {
        last=min(a/(a/i),b/(b/i));
        sum+=1LL*(a/i)*(b/i)*(f[last]-f[i-1]);
    }
    return sum;
}

int main()
{
    f[1]=1;
    for(int i=2;i<=MN;i++)
    {
        if(!b[i]) f[i]=-1,s[++num]=i;
        for(int j=1;s[j]*i<=MN;j++)
        {
            b[s[j]*i]=1;
            if(i%s[j]==0) break;
            f[s[j]*i]=-f[i];
        }
        f[i]+=f[i-1];
    }
    n=read();m=read();if(n>m)swap(n,m);
    for(int p=1;p<=n;p++) ans+=1LL*2*p*calc(p);
    printf("%lld\n",ans-1LL*n*m);
    return 0;
}